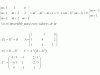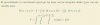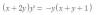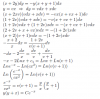-
Hola muy buenas....
Alguien puede ayudarme.
** Calcule el volumen por integración triple del tetraedro limitado por el plano (x/a)+(y/b)+(z/c)=1 y los planos coordenados. (∫ ∫ ∫)
. Por favor lo necesito, mas que se necesito ayuda planteando la integral triple con sus límites, esa integral la puedo resolver yo, ya que eso es lo un poco tedioso. Gracias
-
buenas quisiera saber si me explican como hallar la funcion inversa de f(x)=(e^x - 1)/(e^x + 1)
Gracias de antemano
Ángel
el 29/8/17Mira este vídeo desde 00:01 hasta 07:30
Antonio Silvio Palmitano
el 29/8/17Comienza por observar que el dominio de la función es el conjunto de los números reales.
Luego, plantea para un elemento y perteneciente a la imagen de la función:
y = f(x), sustituyes la expresión de la función en el segundo miembro y queda:
y = (ex - 1)/(ex + 1), haces pasaje de divisor como factor y queda:
y*(ex + 1) = ex - 1, distribuyes en el primer miembro y queda:
y*ex + y = ex - 1, haces pasajes de términos y queda:
y*ex - ex = - y - 1, extraes factor común en el primer miembro y queda:
ex*(y - 1) = - y - 1, haces pasaje de factor como divisor y queda:
ex = (-y - 1)/(y - 1), observa que y debe ser distinto de 1 y que la expresión del segundo miembro debe ser positiva,
luego compones en ambos miembros con la función inversa de la función exponencial natural y queda:
x = ln[ (-y - 1)/(y - 1) ],
luego permutas variables y queda:
y = ln[ (-x - 1)/(x - 1) ],
que es la expresión de la función inversa a la función cuya expresión tienes en el enunciado:
f-1(x) = ln[ (-x - 1)/(x - 1) ].
Luego, para determinar el dominio de la función inversa (que debe coincidir con la imagen de la función), observa que el argumento del logaritmo debe ser estrictamente mayor que cero, por lo que tienes dos opciones:
a)
-x - 1 > 0 y x - 1 > 0, haces pasajes de términos numéricos en ambas inecuaciones y quedan:
-x > 1 y x > 1, multiplicas por -1 en ambos miembros de la primera inecuación (observa que cambia la desigualdad) y quedan:
x < -1 y x >1, que conducen al subintervalo vacío, ya que las inecuaciones son incompatibles:
Sa = Φ;
b)
-x - 1 < 0 y x - 1 < 0, haces pasajes de términos numéricos en ambas inecuaciones y quedan:
-x < 1 y x < 1, multiplicas por -1 en ambos miembros de la primera inecuación (observa que cambia la desigualdad) y quedan:
x > -1 y x <1, que conducen al subintervalo:
Sb = (-1,1);
luego, tienes que dominio de la función inversa queda expresada:
D(f-1) = Sa u Sb = Φ u (-1,1) = (-1,1).
Espero haberte ayudado.
-
Buenas a todos, queria saber como resolver (sen+cos)²= sen²+2 sen cos +cos²
graciaas por la ayuda ^^
Antonio Silvio Palmitano
el 29/8/17Tienes que desarrollar el cuadrado de la suma que tienes en el primer miembro:
(senx + cosx)2 = (senx + cosx)*(senx + cosx) = distribuyes y queda:
= sen2x + senx*cosx + cosx*senx + cos2x = reduces los términos centrales y queda:
= sen2x + 2*senx*cosx + cos2x.
Espero haberte ayudado.
-
Heyyy chicos
Tengo este ejercicio...iguale las dos ecuaciones pero llego a una ecuación en donde me queda una ecuación de ax^2+bx+c y no se que mas hacer
gracias por su ayuda
Antonio Silvio Palmitano
el 29/8/17Plantea el sistema de ecuaciones:
y = mx
y = x/(x2+1),
igualas ambas expresiones y queda:
mx = x/(x2+1), haces pasaje de divisor como factor y queda:
mx(x2+1) = x, distribuyes en el primer miembro, haces pasaje de término y queda:
mx3 + mx - x = 0, extraes factor común en el primer miembro y queda:
x(mx2 + m - 1) = 0,
luego, observa que por anulación de un producto tienes dos opciones:
a)
x = 0, que al reemplazar en las ecuaciones de las curvas conduce a: y = 0,
por lo que tienes que un punto de intersección entre las curvas es: A(0,0);
b)
mx2 + m - 1 = 0, haces pasajes de términos y queda:
mx2 = -m + 1, observa que m debe ser distinto de cero (y que también m debe ser distinto de 1, porque si lo es conduce a la solució x = 0 que ya hemos estudiado),
luego haces pasaje de factor como divisor y queda:
x2 = (-m+1)/m, haces pasaje de potencia como raíz y queda:
x = ±√( (-m+1)/m ),
luego, observa que el argumento de la raíz debe ser mayor o igual que cero para obtener más puntos de intersección entre las curvas, por lo que tienes dos opciones:
b1)
- m + 1 > 0 y m > 0, haces pasaje de término en la primera inecuación y quedan:
- m > - 1 y m > 0, multiplicas por -1 en ambos miembros de la primera inecuación (observa que cambia la desigualdad) y quedan:
m < 1 y m > 0, por lo que tienes la condición:
0 < m < 1;
b2)
- m + 1 < 0 y m < 0, haces pasaje de término en la primera inecuación y quedan:
- m < - 1 y m < 0, multiplicas por -1 en ambos miembros de la primera inecuación (observa que cambia la desigualdad) y quedan:
m > 1 y m < 0, que son inecuaciones incompatibles.
Luego, puedes concluir que las dos curvas delimitan una región para valores de m estrictamente comprendidos entre cero y uno.
Espero haberte ayudado.