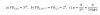-
Álvaro
el 9/6/17El vector director es (1,-2) y pasa por P, luego:
Alguien me puede explicar esto mejor.
Os pongo el enunciado:
Calcula la recta perpendicular a:
x = -1 + 2t
y = 5 + t
que pasa por el punto (-1,0).
Antonio Silvio Palmitano
el 9/6/17Tienes las ecuaciones cartesianas paramétricas de la recta r:
x = - 1 + 2t
y = 5 + t
con t ∈ R,
y recuerda que la información inmediata es:
un punto perteneciente a la recta, cuyas coordenadas son los términos independientes: A(-1,5),
el vector director, cuyas componentes son los coeficientes que multiplican al paámetro t: u = < 2 , 1 >.
Luego, tienes que el vector w = < a , b >, director de la recta parpendicular r, debe ser perpendicular a u,
por lo que planteas que su producto escalar es igual a cero:
u • w = 0, sustituyes y queda:
< 2 , 1 > • < a , b > = 0, desarrollas el producto escalar y queda:
2a + b = 0, de donde puedes despejar: b = - 2a,
luego reemplazas en la expresión del vector w y queda:
w = < a , - 2a > = a * < 1 , - 2 >,
por lo que tienes que un vector director de la recta perpendicular puede ser: w = < 1, - 2 >.
Luego, como tienes que el punto B( - 1 , 0 ) pertenece a la recta,
puedes plantear sus ecuaciones cartesianas paramétricas:
x = - 1 + p
y = 0 - 2p,
con p ∈ R.
Espero haberte ayudado.
-
Veronica Palacin Canturiense
el 9/6/17Buenas tardes, alguien me puede ayudar con este problema de probabilidad. Muchas gracias!
Un examen de tipo test consta de 10 preguntas, cada una con 3 respuestas posibles , de las cuales sólo una es correcta. ¿Cuántas posibles respuestas distintas se pueden dar al azar? ¿Cuántas de ellas tendrán exactamente 7 respuestas correctas? ¿Cuál es la probabilidad de tener 7 respuestas correctas?
-
Osmaynis Derken González
el 9/6/17
Tengo un arroz con mango con esto , alguien me podría ayudar, necesito entender bien, se los agradecería
a) Encuentre el árbol final T si los números se insertan en un árbol binario de búsqueda vació T.
b) Considere el árbol T construido en el ítem a).Si al árbol se elimina ITEM=35, encuentre el nuevo árbol T.
c) Encuentre el montículo final H si los números se interceptan en un minheap (Montículo mínimo ) vació H.
Antonius Benedictus
el 16/6/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
fernando
el 9/6/17
quiero hacer esa operacion con la calculadora, alguien me dice si puede ?
-
Osmaynis Derken González
el 9/6/17Hola buenas , alguien me podría ayudar plis
1- Construya el árbol de la expresión algébrica
2-Escriba la forma de prefijo.
Muchas gracias de ante mano gracias.
Antonius Benedictus
el 9/6/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Osmaynis Derken González
el 9/6/17 -
Javi Santos
el 9/6/17Tengo un ejercicio que es (𝑓·𝑔)(𝑥) de 𝑓(𝑥)=𝑥−3/2𝑥+1 𝑖 𝑔(𝑥)=4𝑥2−1, pero no se si el resultado está bien, me da -8x2+3/2x+1, ya que solo he multiplicado g(x) por x-3 pero por el de abajo no.
Antonio Silvio Palmitano
el 9/6/17Tienes las expresiones de las funciones:
f(x) = (x - 3)/(2x + 1), cuyo dominio es: Df = R - { 1/2 };
g(x) = 4x2 - 1 = factorizas = (2x - 1)(2x + 1), cuyo dominio es: Dg = R.
Luego, por definición de función producto de dos funciones, tienes:
(f*g)(x) = f(x) * g(x) = (x - 3)/(2x + 1) * (2x - 1)(2x + 1) = (x - 3)(2x - 1)(2x + 1) / (2x + 1),
luego simplificas y la expresión de la función producto queda:
(f*g)(x) = (x - 3)(2x - 1) = 2x2 - x - 6x + 3 = 2x2 - 7x + 3, cuyo dominio es: D = Df ∩ Dg= R - { 1/2 }.
Espero haberte ayudado.
-
Julio
el 9/6/17Como factorizo x^2-2/3 x-17/3
Antonio Silvio Palmitano
el 9/6/17Plantea la ecuación:
x2 - (2/3)x - 17/3 = 0, multiplica por 3 en todos los términos de la ecuación y queda:
3x2 - 2x - 17 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente, y sus soluciones son:
x1 = ( 2 + √(208) )/6 = ( 2 + 4√(13) )/6 = ( 1 + 2√(13) )/3,
x2 = ( 2 - √(208) )/6 = ( 2 - 4√(13) )/6 = ( 1 - 2√(13) )/3.
Luego, tienes que el coeficiente principal del polinomio del enunciado es 1,
y que los valores x1 y x2 son raíces del polinomio,
por lo que tienes que ( x - ( 1 + 2√(13) )/3 ) y ( x - ( 1 - 2√(13) )/3 ) son sus factores,
y la expresión factorizada queda:
P(x) = 1*( x - ( 1 + 2√(13) )/3 )*( x - ( 1 - 2√(13) )/3 ) ≅ 1*(x - 2,737)*(x + 2,070).
Espero haberte ayudado.
-
cesar
el 9/6/17Hola quien me puede ayuda con un ejercicio de ecuacion diferencial de segundo orden utilizando metodo de coeficiientes indeterminados
el ejercicio es el siguiente y"+y´-6y=x senx
Antonio Silvio Palmitano
el 9/6/17Vamos por etapas.
1°) Plantea la ecuación homogénea asociada:
yh ' ' + yh ' - 6yh = 0, cuya ecuación característica es:
r2 + r - 6 = 0, y sus raíces son: r1 = - 3 y r2 = 2;
luego, la expresión de la solución general de la ecuación homogénea queda:
yh = Ae-3x + Be2x (1).
2°) Observa que los términos no son polinómicos, ni seno, ni coseno,
por lo que puedes plantear como solución particular:
Y = axsenx + bsenx + cxcosx + dcosx, cuya derivada primera queda:
Y ' = asenx + axcosx + bcosx + ccosx - cxsenx - dsenx = - cxsenx + (a - d)senx + axcosx + (b + c)cosx,
y su derivada segunda queda:
Y ' ' = - csenx - cxcosx + (a - d)cosx + acosx - axsenx - (b + c)senx = - axsenx + (- b - 2c)senx - cxcosx + (2a - d)cosx;
luego sustituyes en la ecuación particular y queda:
(- a - c + 6a)xsenx + (- b - 2c + a - d + 6b)senx + (- c + a + 6c)xcosx + (2a - d + b + c + 6d)cosx = xsenx,
reduces términos semejantes en los coeficientes y queda:
(5a - c)xsenx + (a + 5b - 2c - d)senx + (a + 5c)xcosx + (2a + b + c + 5d)cosx = 1xsenx + 0senx + 0xcosx + 0cosx,
luego, igualas coeficiente a coeficiente y tienes el sistema de cuatro ecuaciones con cuatro incógnitas:
5a - c = 1
a + 5b - 2c - d = 0
a + 5c = 0
2a + b + c + 5d = 0
Luego, queda que resuelvas el sistema, determines los valores de los coeficientes,
y expreses la solución particular (te dejo la tarea).
3°) Expresas la solución general de la ecuación diferencial del enunciado,
como la suma entre la solución general homogénea más la solución particular:
y = yh + Y.
Espero haberte ayudado.
