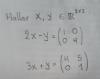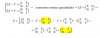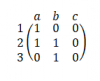-
Caio Medeiros
el 26/10/19Caio Medeiros
el 26/10/19Antonius Benedictus
el 26/10/19Caio Medeiros
el 26/10/19 -
Que sucede si la derivada de una función me da como resultado 0? quiere decir que su f(x) no crece ni decrece si no que es continua, como una recta?
Miguel Fuego
el 26/10/19 -
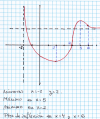
Buenas tardes, alguien me puede corregir esto, se que el dibujo esta mal, no puedo determinar el maximo, creo que hay un error en el enunciado en la segunda derivada f''(x)<0 (4, infi), diria que el infinito es un 6.
gracias adelantadas.
Quiroga
el 26/10/19Jose Ramos
el 26/10/19Los límites me informan por donde anda la gráfica cuando x tiende a -2 (+infinito) (asíntota vertical) y cuando x tiene a infinito la función tiende a 2 (Asíntota horizontal). El mínimo relativo es el punto donde la función cambia de decrecer a crecer (f '<0 a f ' >0) y el máximo donde cambia de crecer a decrecer (f '>0 a f ' <0). Los puntos de inflexión se producen donde la función cambia de cóncava a convexa o viceversa (f''<0 a f''>0 o viceversa)
-
ola, alguien me podría ayudar con este ejercicio de aplicaciones lineales? lo que yo intenté es conseguir las coordenadas de la base canónica respecto a la base (1,2,3),(0,-1,2),(1,0,3) pero a partir de aí no se me ocurre como seguir y no sé muy bien que estoy haciendo
-
Hola a todos!!
Aqui tengo un cálculo con logaritmos y me pide que resuelva aplicando propiedades.
El resultado,segun el libro, es 2/9. Pero no me da..incluso al haber intentado varios caminos diferentes y aplicando las propiedades. Me ayudan?
Muchas Gracias! Patri
Miguel Fuego
el 26/10/19El problema está en la aplicación de dos de las propiedades de los logaritmos. En la segunda fila, puedes separar
log (3 *√(1/2)) = log3 + log(√(1/2))
Esto es importante porque, solo puedes pasar un exponente multiplicando fuera de un logaritmo si el exponente afecta a todo el contenido del logaritmo.
Con eso, el segundo término queda:
log√(1/2) = log ((1/2)1/2) = log(2-1/2) = -1/2 log(2)Recuerda que una raíz cuadrada es equivalente a un 1/2 en el exponente.
Imagino que con eso ya sabrás hacerlo, pero si no es así, dime y vemos cómo seguir.
-
Miguel Fuego
el 26/10/19a=2 es el valor para el cual la matriz tiene rango menor que 4. Coge una sección de 3x3 para comprobar que tiene determinante distinto de cero (si el determinante fuese 0, la matriz podría ser de rango 2). Como cogiendo una sección de 3x3 el determinante ha salido distinto de cero, la matriz es de rango 3.
-
Miguel Fuego
el 26/10/19Una forma de calcular determinantes de 4x4 es cogiendo cada elemento de una columna y multiplicarlo por el determinante de la matriz (de un orden inferior) que no contiene ni a la columna en cuestión, ni a la fila donde está cada elemento. O sea, una suma de 4 términos.
Han seleccionado una columna que tiene 3 ceros, de forma que 3 de esos cuatro términos desaparecen y solo queda el que ves en el ejercicio. Fíjate que la matriz que multiplica a '1' es la que tenías en 4x4 sin la fila y la columna donde aparece ese '1'.