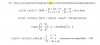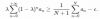-
Fran Ros
el 8/5/17 -
carmela
el 8/5/17Hola. Me piden hallar el area y perímetro de esta corona circular, pero es que el dibujo me despista al estar cortada. Me ayudais?
Neofito 007
el 8/5/17Lo que allí puedes observar es que 10 es el radio mayor, es la distancia desde el centro hasta el borde exterior.
Además ver que 6 es el ancho de la corona y este es la diferencia del radio mayor menos el radio menor.
Siendo el radio mayor 10 y la diferencia de radios 6, concluye que el radio menor es 4
Observar además que esa figura es 3/4 de una corona circular completa , el área es
(3/4) [pi*10^2 - pi*4^2 ]
Para el perímetro es algo similar.
En el borde exterior es 3/4 de una circunferencia de radio 10
En el borde interior es 3/4 de una circunferencia de radio 4
A esto hay que sumarle 2 cortes de 6 unidades y con eso cerramos la figura
La suma total es el perímetro, quedan los cálculos para ti, saludos
.
-
Guillem De La Calle Vicente
el 8/5/17Teorema uniforme tauberiano
Sea ϵ>0..
Me pregunto si lo siguiente es cierto:
Existe λ0 ∈ (0,1), tal que para todos λ≤λ0 y todos (an)∈[0,1]N existe N∈N tal que
David
el 12/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Juan Antonio
el 8/5/17Hola, estuve mirando vídeos, pero sigo sin saber. Ayuda por favor! Gracias de antemano.
Antonio Silvio Palmitano
el 8/5/17Vamos con una orientación.
Observa que el dominio de la función es D = R - {0} = (-∞,0) u (0,+∞).
Luego, observa que la expresión de la función puede escribirse:
f(x) = (x2 + 1)/x = x2/x + 1/x = x + 1/x;
y la expresiones de las derivadas primera y segunda quedan:
f ' (x) = 1 - 1/x2,
f ' ' (x) = 2/x3.
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo).
f ' (x) = 0, sustituyes y queda:
1 - 1/x2 = 0, de donde puedes despejar: x = - 1 y x = 1, que pertenecen al dominio de la función.
Luego, plantea la condición de posible punto de inflexión:
f ' ' (x) = 0, sustituyes y queda:
2/x3 = 0, haces pasaje de divisor como factor y queda:
2 = 0, que es una identidad absurda, por lo que tenemos que la gráfica de la función no presenta puntos de inflexión.
Luego, divides el dominio en subintervalos limitados por los puntos críticos y posibles inflexiones que has determinado, eliges un representante en cada subintervalo y evalúas los signos de las derivadas primera y segunda:
(-∞,-1), representado por x = -2, y para él tienes: f ' (-2) = 3/4 > 0 y f ' ' (-2) = - 1/4 < 0;
(-1,0), representado por x = - 1/2, y para él tienes: f ' (-1/2) = - 3 < 0 y f ' ' (-1/2) = - 16 < 0;
(0, 1), representado por x = 1/2, y para él tienes: f ' (1/2) = - 3 < 0 y f ' ' (1/2) = 16 > 0;
(1,+∞), representado por x = 2, y para él tienes: f ' (2) = 3/4 > 0 y f ' ' (2) = 1/4 > 0.
Luego, tienes que la gráfica de la función es:
creciente y cóncava hacia abajo en el intervalo (-∞,-1),
decreciente y cóncava hacia abajo en el intervalo (-1,0),
decreciente y cóncava hacia arriba en el intervalo (0,1),
creciente y cóncava hacia arriba en el intervalo (1,+∞).
Luego, tienes que la gráfica de la función presenta:
máximo local en x = - 1, ya que pasa de creciente a decreciente en este punto,
mínimo local en x = 1, ya que pasa de decreciente a creciente en este punto,
y observa que el cambio de concavidad corresponde a x = 0, que no pertenece al dominio de la función.
Espero haberte ayudado.
-
Mónica
el 8/5/17Hola, ¿Qué tal?. Necesito ayuda con esta pregunta:
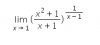tengo que resolverla con L'Hopital, y la profesora puso 4 posibles respuestas: 
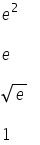Pero, al intentar resolver el ejercicio, me dio un resultado distinto a cualquiera de las opciones. ¿Será que me pueden ayudar? No sé si es que yo tengo un error o es que los resultados no están buenos. Muchas gracias. 
Antonio Silvio Palmitano
el 8/5/17Llamemos L a la expresión del límite,y planteamos su logaritmo:
lnL = Lím(x→1) ( 1/(x-1) )*ln( (x2 + 1)/(x + 1) = Lím(x→1) ( 1/(x-1) )*( ln(x2 + 1) - ln(x + 1) ) =
= Lím(x→1) ( ln(x2 + 1) - ln(x + 1) )/(x - 1).
Observa que el numerador y el denominador del argumento del límite tienden los dos a cero,
por lo que derivamos independientemente para aplicar la Regla de L'Hôpital y queda:
lnL = Lím(x→1) ( 2x/(x2 + 1) - 1/(x + 1) )/1 = (1 - 1/2)/1 = (1/2)/1 = 1/2.
Luego, componemos con la función inversa del logaritmo natural y queda:
L = e1/2 = √(e).
Espero haberte ayudado.
-
agostina
el 8/5/17Si a un rectángulo se le aumenta en un 10% la medida de su base y en un 20% la medida de su altura ¿En que porcentaje aumentará la medida de su área?
-
María
el 8/5/17Hola, he visto el vídeo de teoría de los ejercicios de tamaño de una muestra, pero sigo sin entender cual sería el procedimiento de este ejercicio
Queremos determinar el porcentaje de estudiantes que necesitan gafas. De un estudio realizado hace tres años sabemos que el 65 % de ellos usaban gafas.
a) ¿Qué tamaño de muestra debemos coger para cometer un error máximo del 5 % con un nivel de riesgo del 5 %?
b) Si no tenemos información previa, ¿qué tamaño de muestra debemos tomar?
Alguien podría ayudarme? muchas gracias!!
-
nohelia catalina fuentes cruz
el 8/5/17
me pueden decir porque en esta ecuacion el radio es igual a 2 ?
Antonius Benedictus
el 8/5/17
Neofito 007
el 8/5/17Si es tangente al eje "y" entonces la distancia del centro al punto de tangencia (eje "y") te da el radio (esto por geometría básica)
La distancia de un punto al eje " y" esta dado por el valor absoluto de la abscisa , que en este caso es 2.
De forma similar ten en cuenta para otros ejercicios que la distancia de un punto al eje "x" está dado por el valor absoluto de la ordenada de dicho punto
-
JON IRIGOYEN UBIRIA
el 8/5/17Hola, buenas tardes:
Me gustaria saber si tenéis algún video con la explicación de los expresiones algebraicas y los monomios.
MI hijo está en primero de la ESO y tiene examen sobre ese tema.
Gracias y un saludo
Gema
nohelia catalina fuentes cruz
el 8/5/17https://www.youtube.com/watch?v=4g5Yk0ySyP4
https://www.youtube.com/watch?v=fyoP9EWxZRE
hola que bueno encontrar una mama :) hay esta los video si quieres puedes ver los otros pero creo que hay esta todo tu tema
-
Ahlam.
el 8/5/17
me podis ayudar el 23 y 25 son los unicos q no les comprendo y son para mañana🙋🙋
Neofito 007
el 8/5/17He resuelto el 23 explicando algunas cosas, pon un poco de tu parte y con la misma idea y con las fórmulas resuelve el 25.
La diferencia es que las bases son hexágonos regulares entonces averiguar como se calcula el área de un hexágono regular en términos de su lado.
Área hexagono = (3/2)(L^2) * sqrt (3)
Para lo demás indicó en el ejercicio que adjunto sigue la Misma idea
