-
Ariadna
el 3/5/17 -
marmanmar
el 3/5/17 -
Elena Olivares de Paz
el 3/5/17Buenas me podeis ayudar con este ejercicio ,
1 . ¿Cuánto tiene que valer e para que la función f(x)=xlnx-ax tenga en el punto de abcisa e , una recta tangente paralela a la bisectriz del primer cuadrante?
Antonio
el 3/5/17 -
Alejandra Nuero Zahonero
el 3/5/17 -
IT'SMahel YT
el 3/5/17 -
Natalia
el 3/5/17Hola me podeis ayudar con este ejercicio, se el planteamiento pero el resultado no meda nada coherente.
Gracias
3.- Si se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 80 Euros/m y la de los otros 10 Euro/m, halla el área del mayor campo que puede cercarse con 28800 Euros.
Antonio
el 3/5/17sea x el lado del camino e y el otro lado
la función a optimizar es:
A=x·y
y la condición es que: 80x+10x+10y+10y=28800 (recuerda que son 4 lados)
80x+10x+10y+10y=28800 => 90x+20y=28800 => 9x+2y=2880 => y=(2880-9x)/2
A=x·y = x·((2880-9x)/2) = (2880x-9x2)/2
A'= (2880-18x)/2
A'=0 => (2880-18x)/2 => 2880-18x=0 => x=160
A''=-18/2= -9
A''(160)= -9<0 => Máx
y=(2880-9·160)/2=720
El terreno debe tener 160 metros pegados a la carretera y 720 metros de fondo
y su área será de 160·720=115200 metros cuadrados
-
Aleatorius
el 3/5/17Buen día Unicoos, quisiera saber si mi resolución del ejercicio está bien, es decir, si no hay que tener en cuenta una regla de resolución, definir que se está trabajando con complejos o algo similar...
gonzalezlbl
el 3/5/17Tu respuesta es correcta.
Sólo me incomoda algo de estilo: la colocación de los signos de interrogación.
Una vez que comienzas a desarrollar la respuesta, debes agregar signos de igualdad delante de las expresiones. De esta forma indicas que la expresión que estás colocando es igual a la anterior.
√(-9) × √(-16) = √(9) × √(-1) × √(16) × √(-1) =
= 3 × i × 4 × i =
= 12 × i2 =
= 12 × (-1) =
= -12
Saludos.
Aleatorius
el 3/5/17Una duda más, si yo haría lo siguiente, dentro de la raíz multiplico -9 x -16 (por propiedades de las raíces del mismo índice que se multiplican), esto me dará 144 (positivo), y su raíz es 12 (positivo). Cual sería el paso incorrecto?
Dicho de otra forma: se puede aplicar propiedades de las raíces en números complejos?
Antonio
el 3/5/17 -
Marta
el 3/5/17
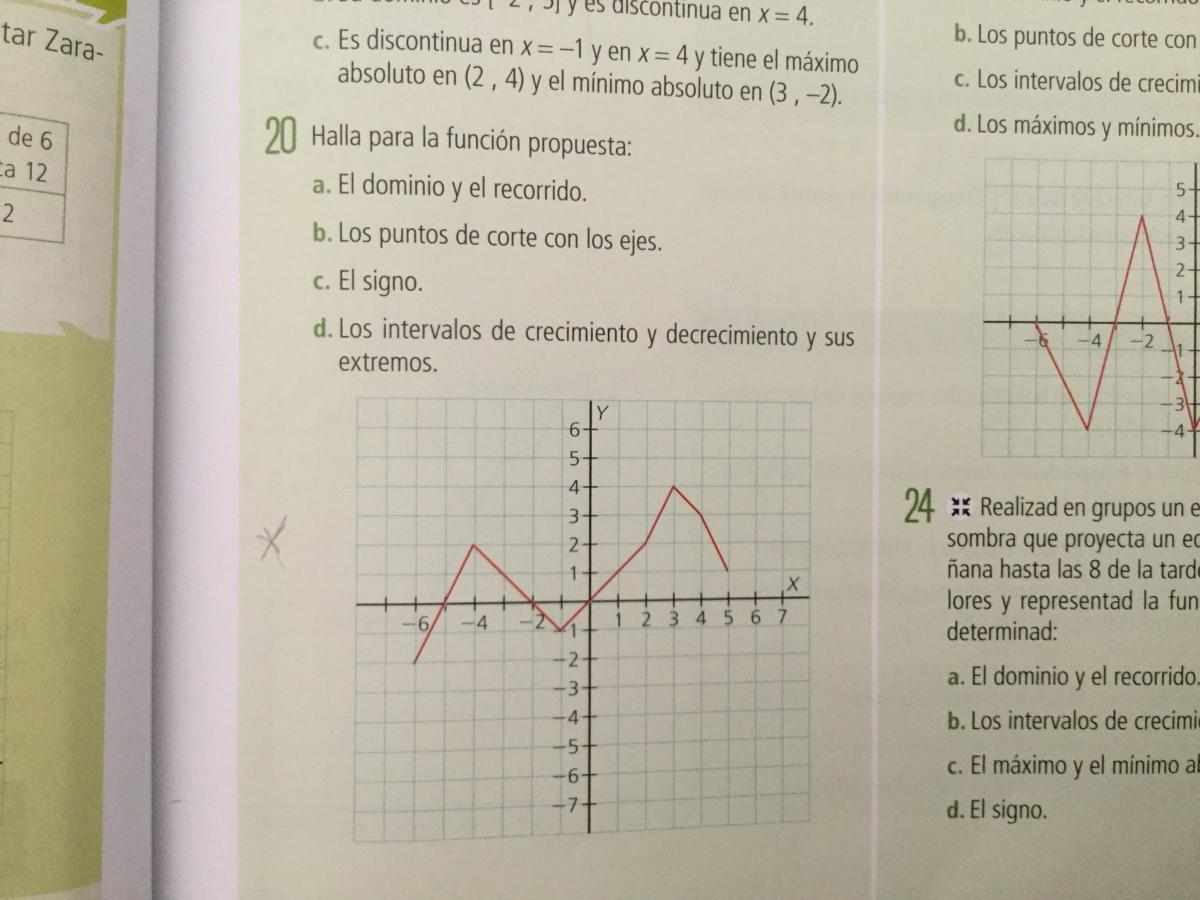
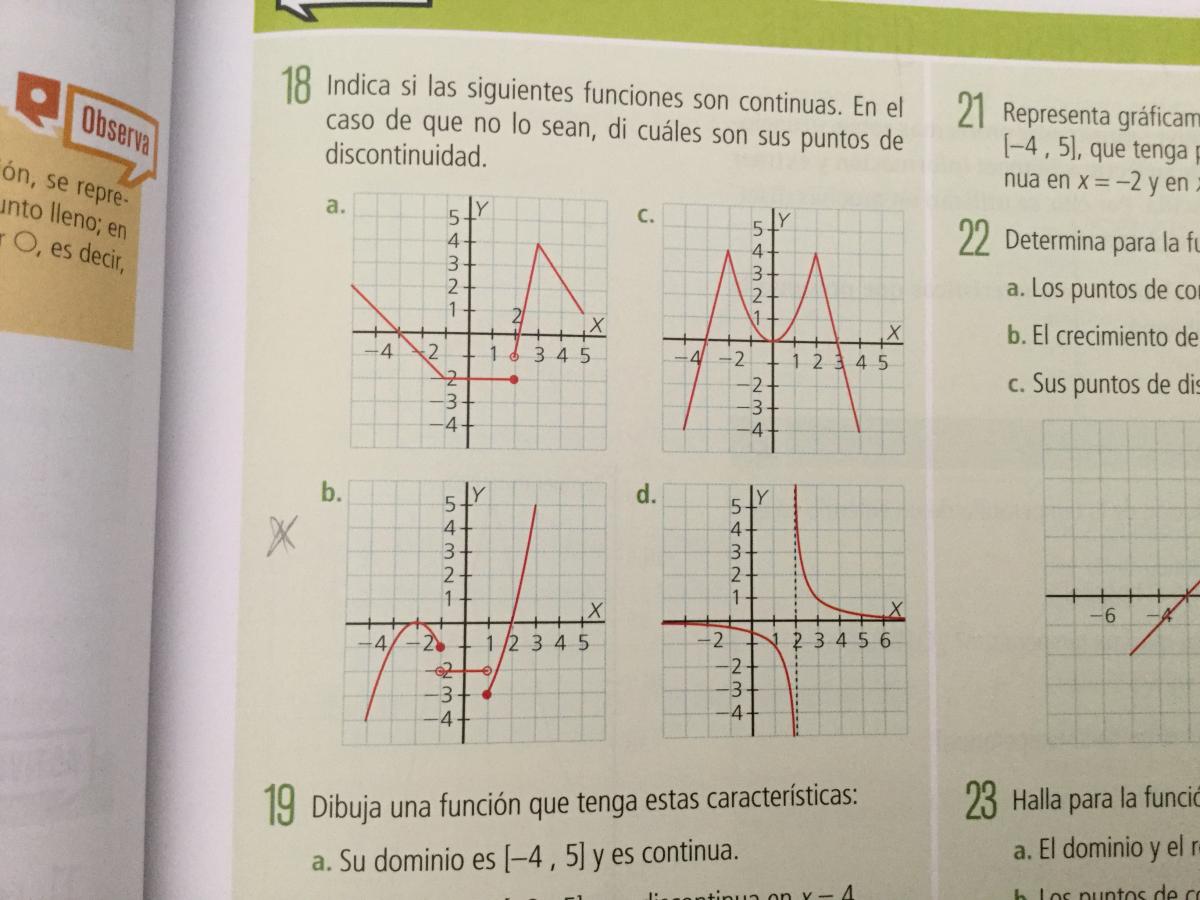
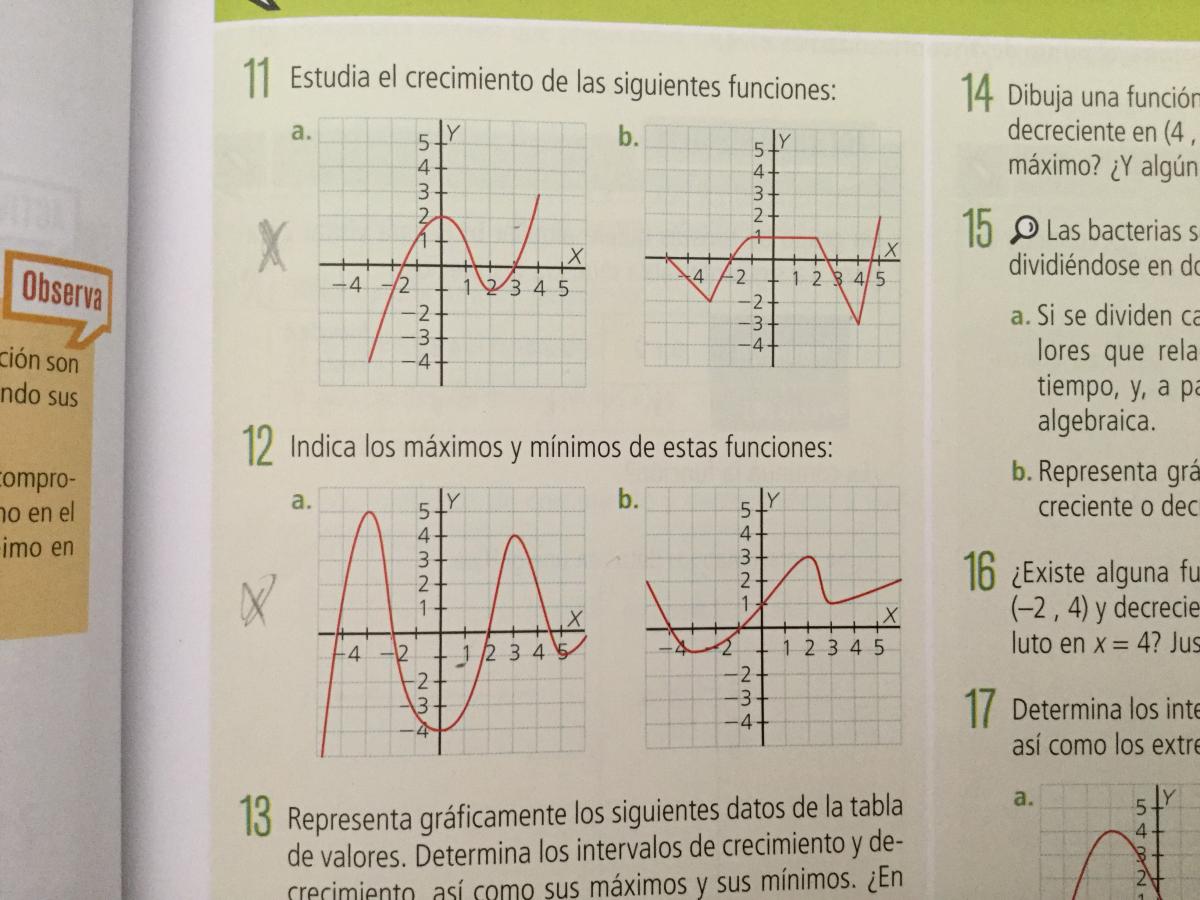
Buenas tardes estoy dando funciones en matemáticas y quería que me explicaran las funciones dependientes y independientes, puntos de corte con los ejes de coordenadas, cuando una función es negativa y positiva,crecimiento y decrecimiento de una función , máximo y el mínimo de una función continuidad y discontinuidad
Antonio
el 3/5/17variable dependiente: y o la que está en el eje vertical
variable independientes: x o la que está en el eje horizontal
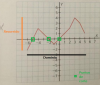
puntos de corte con los ejes de coordenadas: Los puntos donde se corta o se cruza lo rojo (gráfica de la función) con lo negro (ejes cartesianos)
una función es negativa cuando está por debajo del eje horizontal
y es positiva cuando está por encima del eje horizontal
crece cuando sube (de izqda a dcha )
decrece cuando baja (de izqda a dcha )
máximo cuando hay un pico
mínimo cuando hay una depresión
continuidad cuando se puede pintar sin quitar el lápiz del papel
discontinua donde se levanta el lápiz para pintarla
Antonio
el 3/5/17 -
penelope
el 3/5/17alguien me podria explicar como resolver este problema de matriz jacobiana. gracias de ante mano :)
Antonio
el 3/5/17f(x,y,z)=(f1(x,y,z),f2(x,y,z))
f1(x,y,z)=7z+6y2+2x2
f2(x,y,z)=(z+7)/(2y2+2x2+1)
Es derivar cada una de las dos componentes respecto a cada una de las tres variables
df1/dx= d(7z+6y2+2x2)/dx=4x
df1/dy=d(7z+6y2+2x2)/dy=12y
df1/dz=d(7z+6y2+2x2)/dz=7
df2/dy=d((z+7)/(2y2+2x2+1))/dx=(0-4x(z+7))/(2y2+2x2+1)2=(-4xz-28x)/(2y2+2x2+1)2
df2/dz=d((z+7)/(2y2+2x2+1))/dy=(0-4y(z+7))/(2y2+2x2+1)2=(-4yz-28y)/(2y2+2x2+1)2
df2/dx=d((z+7)/(2y2+2x2+1))/dz=((2y2+2x2+1)-0)/(2y2+2x2+1)2=(2y2+2x2+1)/(2y2+2x2+1)2=1/(2y2+2x2+1)
por lo tanto:
4x 12y 7
Jf(x,y,z)= ( )
(-4xz-28x)/(2y2+2x2+1)2 (-4yz-28y)/(2y2+2x2+1)2 1/(2y2+2x2+1)
Antonio
el 3/5/17 -
anaespo
el 3/5/17
