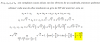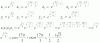-
Álvaro
el 22/4/17Buenas David,
Me gustaría que subieses vídeos de Estadística para 2 bachillerato ( Distribución Normal, Estadística Indiferencial, Distribución en el muestreo, Intervalos de confianza,...)
Espero que lo leas y lo tomes en cuenta por favor, sería de una gran ayuda, un gran abrazo!!!!
-
jose
el 22/4/17 -
jose
el 22/4/17 -
Laura Muñoz Fernandez
el 22/4/17¿Cuándo estamos aplicando el teorema de Rolle siempre estamos aplicando a su vez el teorema de Bolzano?
Ángel
el 22/4/17No.
Una cosa es una y otra cosa es otra :D
Aunque se pueden usar a la vez para por ejemplo averiguar el número de raíces de una función (creo recordar que en un vídeo David dijo algo así como que era conocido como "Rollzano")
-
Andres Valenzuela
el 22/4/17
Hola!!
Buen día. Pido ayuda en un sistema de "ecuaciones polares" y "Área entre curvas"
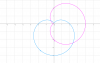
// Graficar la región interior al cardiode r = 2 + 2 Cos (θ) y exterior al cardioide r = 2 - 2 Sen (θ) y determinar el área de la misma. Además determine los puntos de intersección de las curvas.
Resolviendo el sistema de ecuaciones polares por igualación queda___
2 + 2 Cos (θ) = 2 - 2 Sen (θ)
2 Cos (θ) = - 2 Sen (θ)
Tan (θ) = -1
θ = arctan (-1) (La tangente solo es negativa en el segundo y cuarto cuadrante) y mi Referencial y a mi parecer creo que es necesario el Referencial: 0 ≤ θ ≤ 2π
( θ = (3/4)π r = 2 - √2 ) y ( θ = (7/4)π r = 2 + √2 )
Mi duda va aquí: (Ojo) Hay otro punto en común entre las curvas, sin embargo no apareció en las ecuaciones el punto (0,0). Y las curvas tienen en común en ese punto, se lo ve en la grafica.
¿Porque este valor no apareció en mis ecuaciones?
// La curva ROSADA corresponde a la primera ecuación.
Ayúdenme también a encontrar el área pedida.
Gracias de antemano. SALUDOS
Antonio Silvio Palmitano
el 22/4/17Debes tener en cuenta que en coordenadas polares el origen queda descrito con la ecuación r = 0, que es independiente del argumento θ.
Observa que si reemplazas, las ecuaciones quedan:
0 = 2 + 2*cosθ, de donde despejas: - 1 = cosθ, y tienes: π = θ, que representa al origen de coordenadas, pero presentado como un punto perteneciente a la semirrecta cuya ecuación es θ = π (que coincide con el semieje cartesiano x negativo), cuya distancia al polo (origen) es igual a cero;
0 = 2 - 2*senθ, de donde despejas: 1 = senθ, y tienes: π/2 = θ, que representa al origen de coordenadas, pero presentado como un punto perteneciente a la semirrecta cuya ecuación es θ = π/2 (que coincide con el semieje cartesiano y positivo), cuya distancia al polo (origen) es igual a cero.
Siempre es conveniente estudiar qué ocurre con r = 0 cuando trabajamos con ecuaciones con coordenadas polares, para ver si el polo (origen de coordenadas) pertenece o no pertenece a las curvas que son gráficas de dichas ecuaciones, y en este caso tenemos que pertenece a las dos gráficas.
Espero haberte ayudado.
-
ALOFRE
el 22/4/17 -
Deidara Stick.
el 22/4/17Hola de nuevo amigos únicoos
Disculpad la molestia, pero necesito ayuda en otro problema que no logro resolver. El cual trata de números complejos...
Ayuda por favor.
Nuevamente Gracias.
-
Laura Muñoz Fernandez
el 22/4/17Halla el valor de los números reales a y b sabiendo que la pendiente de la recta tangente a la curva de ecuación y=ax2+bx en el punto P(2,2) vale 5.
He mirado el vídeo de la ecuación de la recta tangente pero no he encontrado ningún ejercicio parecido, me podéis ayudar?
-
Nerea
el 22/4/17
