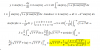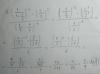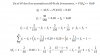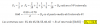-
Alexandra Jerí
el 21/4/17ayuda con este ejercicio...
La recta y=2x+4 intercepta al eje de ordenadas en el punto M. Sea P un punto de dicha recta de modo que el triangulo OMP tiene altura h respecto al vertice M donde O es el origen de coordenadas. Si la abscisa del punto P se hace ilimitadamente grande, determine el valor limite de h
-
Diego Abarca
el 21/4/17
Buenas una consulta como puedo resolverlo? El enunciado pide sacar el área de la superficie obtenida al hacer girar la curva respecto al eje x.
De antemano, gracias.
Neofito 007
el 21/4/17
Diego Abarca
el 21/4/17
Diego Abarca
el 21/4/17
Neofito 007
el 21/4/17La función es
f(x)=Sen(πx)
Su derivada es
f'(x)=πCos(πx)
Eso debes reemplazar en la fórmula que allí muestras y resolver la integral , una vez planteado la integral definida , calcula haciendo un cambio de variable
u=πCos(πx)
Cuyo diferencial es
du= - π^2 Sen(πx) dx
Acomodas tu integral de manera conveniente.
Ando desde el móvil no me es fácil trabajar , sería excelente si en este foro se podría escribir en latex
-
agostina
el 21/4/17Como resuelvo el a y b ?
Ángel
el 21/4/17Disculpa, pero en el a) en el denominador de la fracción "grande", puse un + donde tenía que haber un - delante del 29700
Entonces, la parte final suprímela del folio que te envié y queda así:
(600+79398+85200-29700)/19800=
135498/19800=
67749/9900=
22583/3300=
2053/300= 6.843333333333....
-
Diego Latorre
el 21/4/17No se si lo que voy a hacer este mal, y me den flag, pero tenía que hacerlo.
Ahorita no tengo dudas, pero salí de un parcial que creo que me fue bien, y se lo debo en gran parte a la ayuda de ustedes mientras estudiaba.
No tengo palabras para agradecerles, en especial a Antonio Benito que siempre está muy atento para ayudarme, y obviamente al resto que contribuyen con sus valiosísimos aportes.
Cuesta pensar que aún queda gente como ustedes dispuestos a ayudar, son lo más.
-
Estela Rivero
el 21/4/17ayuda porfa, me piden hallar el conjunto solución de las siguientes ecuaciones: a) 6x al cuadrado - 2y +8=0 b) x al cuadrado=y al cuadrado c) x a la cuarta potencia - 3x al cuadrado+2=0 d) x al cuadrado+10x+6y+9=0
Neofito 007
el 21/4/17Hola estela no se entiende muy claro usa algunos símbolos matemáticos y haz uso de los paréntesis por ejemplo
6x^2 - 2y + 8 = 0
El símbolo ^ significa " elevado a "
Si es así tu ejercicio en ese caso primero saca mitad a todo y queda
3x^2 - y + 4 = 0
Ahora debes despejar para resolver con respecto a x
3x^2 = y - 4
x^2 = (y - 4)/3
Sacas raíz cuadrada y obtienes 2 soluciones
x = sqrt[(y - 4)/3 ]
La otra solución es
x = - sqrt[(y - 4)/3 ]
-
Andrés Cárdenas Tobón
el 21/4/17Sea la urna U (2B, 3N, 4R). Extraemos tres bolas, una a continuación de la otra. La primera es negra, la segunda no se mira y la tercera es blanca. Hallar la probabilidad de que la segunda sea roja.
Agradezco que por favor me expliquen el procedimiento.
La solución debe ser 4/7
Sé un poco sobre el teorema de Bayes, así que por favor, eviten enviar el vídeo. Mi problema es que no sé como asimilar el ejercicio y llevarlo a el teorema de Bayes. -
alvaro garcia
el 21/4/17 -
Jimmy
el 21/4/17
Hola Unicoos , ayúdenme con este ejercicio de Números Complejos por favor
-
Fernando Navarro
el 21/4/17Necesito ayuda con estos ejercicios
1) a través del método de derivación logarítmico resolver: (2/x2+1)cos(2x)
2) derivación en cadena, resolver (la raíz afecta a todo): √ln(x/e-5x)5tan(3x)
Antonio Silvio Palmitano
el 21/4/17Tienes la función cuya expresión es:
y = ( 2/(x2+1) )cos(2x) = ( 2*(x2+1)-1 )cos(2x),
luego compones con la función logaritmo natural en ambos miembros, y en el segundo miembro aplicas la propiedad del logaritmo de una potencia y queda:
lny = cos(2x)*ln( 2*(x2+1)-1 ),
derivas en ambos miembros, y observa que debes aplicar la regla del producto en el segundo miembro, y la regla de la cadena en ambos miembros, y queda:
(1/y)*y ' = - 2*sen(2x)*ln( 2*(x2+1)-1 ) + cos(2x)*( 1 / 2*(x2+1)-1 )*(-2*(x2+1)-2*2x),
luego haces pasaje del divisor y como factor y queda:
y ' = y * [ - 2*sen(2x)*ln( 2*(x2+1)-1 ) + cos(2x)*( 1 / 2*(x2+1)-1 )*(-2*(x2+1)-2*2x) ],
luego sustituyes la expresión de y en función de x y queda:
y ' = ( 2*(x2+1)-1 )cos(2x) * [ - 2*sen(2x)*ln( 2*(x2+1)-1 ) + cos(2x)*( 1 / 2*(x2+1)-1 )*(-2*(x2+1)-2*2x) ].
Espero haberte ayudado.
Ángel
el 21/4/17[√[ln(x/e-5x)5tan(3x)]]´ = u´/ 2√[ln(x/e-5x)5tan(3x)]
Para calcular u´=[ln(x/e-5x) * 5tan(3x)]´ tenemos que ver que es un producto "*", entonces tendremos que hacer
[ln(x/e-5x)]´ * 5tan(3x) + ln(x/e-5x) * [5tan(3x)]´
*[ln(x/e-5x)]´= (e-5x)/(1+5x)
*[5tan(3x)]´= 5tg3x*Ln5*(3/cos23x)
Por lo que u´= [(e-5x)/(1+5x)]*5tan(3x) + (ln(x/e-5x)*5tg3x*Ln5*(3/cos23x)
Concluimos que:
√[ln(x/e-5x)5tan(3x)]´ = {[(e-5x)/(1+5x)]* 5tan(3x) + ln(x/e-5x)* 5tan(3x)*Ln5*(3/cos23x)} / {2√[ln(x/e-5x)5tan(3x)]}
-
Elisabeth Green
el 21/4/17va sobre tests
Hola a todos, soy nueva en este foro y me han puesto un problema que me esta trayendo algo loca la verdad asi que porfavor ruego vuestra ayuda:
En un test de 120 preguntas con 3 opciones posibles, siendosolo una verdadera y los errores no restan
. ¿cuál sería el mínimo número de preguntas que deberia ponerse para acertar y correspondieran al 5 y asegurarme que se sabe con ello la mitad de la asignatura, y su nota no es debida al azar?
Porque claro las 40 primeras preguntas pueden ser por el azar y no deberian por ello contar, pero tampoco 80 acertadas me asegura que se sepa la mitad del temario-
Y reduciendolo a la unidad, si el examen fuera solo una pregunta y una persona se sabe 2/3 del temario, (una parte de cada tema) . sacaria siempre un 10, pues o sabe las dos opciones erróneas y por ende coge la otra, o entre las dos opciones que sabe, esta la verdadera.
Gracias a todos los que me ayuden por favor expliquen la fórmula y el razonamiento empleado de cara a aprender.
