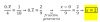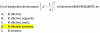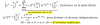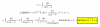Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Sandy Murillo S...
el 22/2/17

Hola unicoos.
Alguien me puede corregir si me he confundido en la respuesta. A mi parecer la respuesta es la alternativa e
Creo que es esa alternativa, ya que para todo x > 0 , la gráfica sería la reflexión de f(x) respecto al eje y ( es decir reflejo la curva respecto al eje y para todo x > 0 ) . Algun error en esto. Gracias a la persona que me ayude. Saludos

••0 voto/s
•
Antonius Benedictus
el 22/2/17
No se distinguen los ejes de coordenadas. Y en este ejercicio es una información básica.

•0 voto/s
•

Cancelar
Deidara Stick.
el 22/2/17

Hola nuevamente, queria pedir de favor que me ayudeis con otro ejercicio si no es mucha molestia por favor. Y muchas gracias de antemano.

••0 voto/s
•
Antonius Benedictus
el 22/2/17

•0 voto/s
•

Cancelar
Deidara Stick.
el 22/2/17

Hola estimados amigos de unicoos, pido ayuda con el problema adjunto de la imagen. Gracias de antemano.

••0 voto/s
•
Antonius Benedictus
el 22/2/17

•0 voto/s
•

Cancelar
Fany Cortes
el 22/2/17

Hola, buenas noches
Alguien me podria explicar este problema de calculo, por favor
Explique porque la funcion es discontinua en el punto dado f(x)= ln|x-2| a=2
Debo sacar limite de 2?

••0 voto/s
•
Antonius Benedictus
el 22/2/17
El límite de f(x) cuando x→2 vale -∞
Hay una asíntota vertical en x=2.
f es, pues, discontinua.

•0 voto/s
•

Cancelar
Jose Hernandez
el 22/2/17

Hola buenas noches. Alquien me puede explicar como se llego a ese resultado? de donde salio o como lllego a
Ln(cosx) + c

••0 voto/s
•
Axel Morales Piñón.
el 22/2/17
Pregúntate José ¿Cuál es la derivada del coseno?

•0 voto/s
•
Axel Morales Piñón.
el 22/2/17
A ver si así lo ves
POR CAMBIO DE VARIABLE
u = cos (x)
du= -sin(x)dx

•0 voto/s
•
Marcos
el 22/2/17

•1 voto/s
•

Cancelar
Anthony Andujar
el 22/2/17

Ayuda algun profesor que sepa realizar estos ejersicios me urgen :S ?

••0 voto/s
•
Antonio Silvio Palmitano
el 22/2/17
Vamos con el primero. Tienes la función cuya expresión es:
y = 2x² + 2, cuya derivada queda: m = dy/dx = y ' = 4x
Luego, proponen la parametrización: x = t, luego sustituyes en la expresión de la función y queda: y = 2t² + 2,
por lo que tenemos:
a)
Ecuaciones cartesianas paramétricas de la gráfica de la función:
x = t
y= 2t² + 2
t ∈ R.
b)
Derivamos con respecto a t en ambas ecuaciones paramétricas y quedan:
dx/dt = 1
dy/dt = 4t
luego planteamos para la pendiente:
m = dy/dx = (dy/dt) / (dxdt) = 4t/1 = 4t (observa que es la expresión parametrizada de la pendiente cuya expresión hemos planteado al comienzo).
Luego, haz el intento con el segundo ejercicio, porque el procedimiento es el mismo, pero cambiarán las expresiones.
Y si te es preciso, no dudes en volver a consultar.
Espero haberte ayudado.

•0 voto/s
•
Anthony Andujar
el 22/2/17
buenas profesor, :s me ayudas hacer el 2 no me sale, o que pasa es que la profesora no lo explico solo mando a resolverlos :/ para que practicaramos

•0 voto/s
•

Cancelar
Manu
el 22/2/17

Me puede decir si está correcto?

••0 voto/s
•
Alejandro
el 22/2/17
Dos cosas, cuando aún no has sustituido el valor de n en este caso siempre debes de poner primero lo de Lim n-->inf
Segundo revísalo porque has cometido varios fallos. Y ese resultado no es posible

•1 voto/s
•
Alejandro
el 22/2/17
Varios fallos por el echo de que 1 elevado a infinito es una indeterminación. Y debes de aplicar una fórmula bastante utilizada para este tipo de casos. En busca en este canal "limites de 1 elevado a infinito" y encontrarás algún ejemplo y también la fórmula que se utiliza para estos casos.

•1 voto/s
•
Antonius Benedictus
el 22/2/17

•1 voto/s
•

Cancelar
juan manuel diaz
el 22/2/17

unicoos, necesito ayuda con la integral de 1/x(x-1)^1/2

••0 voto/s
•
Axel Morales Piñón.
el 22/2/17

•0 voto/s
•

Cancelar
pablo
el 22/2/17

hola estoy repasando temas de subespacios vectoriales y no recuerdo ¿por que una recta o plano para que sean subespacios vectoriales de r3 se necesitan que pasen por el origen?

••0 voto/s
•
Antonius Benedictus
el 22/2/17
Porque en un subespacio vectorial ha de estar siempre el vector nulo, cuya representación geométrica es el origen de coordenadas. por eso, las ecuaciones cartesianas de un subespacio vectorial son lineales (de primer grado) y homogéneas (término independiente nulo), que siempre tienen la solución trivial.

•0 voto/s
•

Cancelar