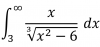-
Buenas tarde:
Tengo solucionado el siguiente problema de trigonometría de 4Eso pero me gustaría vuestra opinión:
Problema:
Calcular el perímetro y el área de un triángulo isósceles en el que el ángulo desigual mide 72º y la medida del lado opuesto a ese ángulo es de 16m.
Solución:
180º-72º-2α= 54º
tag54º=h/8= 11,01m
sen54º= 11,01/a....a=13,60m
perímetro= 2x13,60+16=43,2m
Area= (16x11,01)/2= 88,08m
Gracias
-
Antonio Silvio Palmitano
el 15/2/17Debes aplicar la regla de derivación para un producto de funciones:
y = u*v
y ' = u ' * v + u * v '
En tu ejercicio tienes:
u = 2*cosx, cuya derivada queda: u ' = 2*(- senx) = - 2*senx
v = senx, cuya derivada queda: v ' = cosx
Luego, aplicas la regla y queda:
y ' = - 2*senx*senx + 2*cosx*cosx = reducimos factores = - 2*sen2x + 2*cos2x = extraemos factor común:
= 2*(- sen2x + cos2x) = aplicamos la identidad trigonométrica del coseno del doble de un ángulo = 2*cos(2x).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/2/17Observa que es un límite indeterminado, ya que el numerador y el denominador tienden ambos a cero.
Luego, aplicamos la Regla de L'Hôpital, para lo que derivamos independientemente al numerador y al denominador:
N ' = 4sen(2x)*cos(2x) = 2*2sen(2x)*cos(2x) = aplicamos identidad trigonométrica del seno del doble de un ángulo = 2*sen(4x),
D ' = 3x2 + 2x,
luego, como ambas expresiones tienden a cero, volvemos a derivar independientemente y queda:
N ' ' = 8*cos(4x) (observa que tiende a 8),
D ' ' = 6x + 2 (observa que tiende a 2),
luego, tienes que el límite existe y su valor es: L = 8/2 = 4.
Luego, presentamos el planteo con más formalidad:
L = Lím(x→0) sen2(2x)/(x3 + x2) = aplicamos la Regla de L'Hôpital:
= Lím(x→0) 2*sen(4x)/(3x2 + 2x) = aplicamos la Regla de L'Hôpital:
= Lím(x→0) 8*cos(4x)/(6x + 2) = evaluamos:
= 8*1/(0 + 2) = 8/2 = 4.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/2/17Observa que tienes la ecuación de la recta R:
y + x = - 3, haces pasaje de término y queda su ecuación cartesiana explícita: y = - x - 3, de donde tienes que su pendiente es: mR = -1.
Luego, tienes la expresión de la función:
f(x) = x3 + ax, cuya derivada queda:
f ' (x) = 3x2 + a,
luego, evaluamos para x = 0 y obtenemos la pendiente de la recta tangente:
mT = f ' (0) = a.
Luego, como tenemos en el enunciado que la recta tangente T es perpendicular a la recta R, planteamos la condición de perpendicularidad:
mT = - 1/mR, sustituimos y queda:
a = - 1/(-1) = 1.
Luego, la expresión de la función queda: f(x) = x3 + x,
la ordenada del punto de contacto entre la recta tangente y la gráfica de la función queda: y = f(0) = 0,
luego, tenemos que el punto de contacto tiene coordenadas: A(0,0),
y tenemos que la ecuación de la recta tangente queda: y = x.
Espero haberte ayudado.
-
Hola duda de universidad
Considerar el polinomio de Taylor de grado 3 de f(x) = √x centrado en 4. Dar una cota superior del error que se comete al estimar √6
Antonio Silvio Palmitano
el 15/2/17Observa que el centro de desarrollo es c = 4, y que debemos evaluar la función para x = 6.
Luego, tenemos la función cuya expresión es: f(x) = √(x) = x1/2, luego planteamos sus derivadas hasta el orden 4. las evaluamos y planteamos los coeficientes:
f (0)(x) = x1/2, luego tenemos: a0 = f(4) / 0! = 2/1 = 2,
f(1)(x) = (1/2)x-1/2, luego tenemos: a1 = f(1)(4) / 1! = 1/4,
f(2)(x) = (-1/4)x-3/2, luego tenemos: a2 = f(2)(4) / 2! = - 1/64,
f(3)(x) = (3/8)x-5/2, luego tenemos: a3 = f(3)(4) / 3! = 1/512,
f(4)(x) = (-15/16)x-7/2, luego tenemos: aR = f(4)(z) / 4! =(-5/128)z-7/2, con 4 ≤ z ≤ 6.
Luego, planteamos el Polinomio de Taylor de orden 3 y grado 3:
P(x) = 2 + (1/4)(x - 4) - (1/64)(x - 4)2 + (1/512)(x - 4)3 (1).
Luego, planteamos la expresión del error con la Fórmula de Lagrange:
R(x) = ( f(4)(z) / 4! )(x - 4)4 = ( (-5/128)z-7/2 )(x - 4)4,
luego evaluamos la expresión del error para x = 6:
R(6) = (-5/128)z-7/2 )*24 = (- 5/8)z-7/2 = - 5 / (8z7/2);
luego parsamos a la acotación del error, y para ello planteamos su valor absoluto:
| R(6) | = | - 5 / (8z7/2) | = 5 / 8z7/2 = acotamos (reemplazamos z por 4 que es el extremo menor del intervalo) y queda:
| R(6) | ≤ 5/(8*47/2) = 5/(8*128) = 5/1024 = 0,0048828125.
Luego, el valor aproximado de la función para x = 6 queda planteado:
f(6) ≅ P(6), reemplazamos en las expresiones y queda:
√(6) ≅ 2 + (1/4)(6 - 4) - (1/64)(6 - 4)2 + (1/512)(6 - 4)3 = 2 + 1/2 - 1/16 + 1/64 = 2,453125.
Luego, verificamos con calculadora la validez de la cota de error:
√(6) - P(6) ≅ 0,00363 < | R(6) |.
Espero haberte ayudado.
-
¡Hola! ¿Podrían ayudarme con este ejercicio?
¿Qué es mayor, 4√6 o 3/2 ?
Represéntalos en la recta real.
Gracias desde ya :)
Antonio Silvio Palmitano
el 15/2/17Llamemos:
x = 4√(6), e y = 3/2, y observa que son dos cantidades positivas, luego planteamos:
x4 = ( 4√(6) )4 = 6, e y4 = (3/2)4 = 81/16.
Luego planeamos el cociente:
(y/x)4 = y4/x4 = (81/16) / 6 = 27/32 = 0,84375.
Luego, a partir de la igualdad remarcada, plenteamos:
(y/x)4 = 27/32 < 1,
hacemos pasaje de potencia como raíz en la desigualdad remarcada y queda:
y/x < 1,
luego hacemos pasaje de divisor como facotr (observa que no cambia la desigualdad) y queda:
y < x,
reemplazamos valores y queda:
3/2 < 4√(6).
Puedes verificar con tu calculadora que la desigualdad es verdadera.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/2/17Observa que es una integral impropia (su límite superior de integración es infinito, y las raíces del argumento de la raíz en el denominador no pertenecen al intervalo de integración).
1°)
Plantea la integral indefinida, que puedes resolver por medio de la sustitución (cambio de variable):
w = x2 - 6, de donde tienes: dw = 2x*dx y de donde puedes despejar: dw/2 = x*dx.
Luego sustituyes y la integral indefinidad queda:
Ii = (1/2)*∫ dw/∛(w) = (1/2)*∫ w-1/3*dw = (1/2)*(3/2)*w2/3 + C = (3/4)*w2/3 + C = sustituimos = (3/4)*(x2 - 6)2/3 + C.
2°)
Luego plantea la integral definida entre 3 y un límite genérico a (indicamos con corchetes que debemos evaluar con Regla de Barrow):
Id = [ (3/4)*(x2 - 6)2/3 ] = (3/4)*(a2 - 6)2/3 - (3/4)*(02 - 6)2/3 = (3/4)*(a2 - 6)2/3 - (3/4)*(- 6)2/3 = (3/4)*(a2 - 6)2/3 - (3/4)*∛(36).
3°)
Plantea el límite para x tendiendo a +infinito de la expresión de la integral definida:
I = Lím(x→+∞) ( (3/4)*(a2 - 6)2/3 - (3/4)*∛(36) ) = +∞ (observa que el primer término tiende a +infinito y que el segundo término es constante).
Por lo tanto, concluimos que la integral impropia del enunciado es divergente.
Espero haberte ayudado.