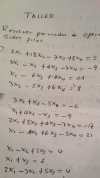-
Deidara Stick.
el 14/2/17Hola, buen día.
Alguien me podría ayudar con el siguiente ejercicio, relacionado con la geometria analítica.
Gracias de antemano....
Deidara Stick.
el 14/2/17 -
Rocio Redero Conde
el 14/2/17Buenos días.
Me podéis ayudar con el ejercicio siguiente. Es de 4 ESO.
-
Infam Salem
el 14/2/17Buenas disculpen la molestia tengo un ejercicio que no puedo resolver o practicamente le estoy dando mucha vuelta...
El ejercicio es asi, El limite de x cuando tiende a infinito de (x+1)^(x^2)... No se si debo realizarlo para que me de e, o directamente infinito elevado a la infinito... Gracias por la ayuda.. -
Juan Daniel Fontalvo Rivas
el 14/2/17
el problema ese el siguiente, me piden que las resuelva por el metodo de reduccion, pero me lo explicaron con tres letras ( x y z ) y ahora veo esos ejercicios y solo tiene xsub1 y noc si se debe hacer de la misma forma que se aplica con el metodo de reduccion no importan si son de la misma letra? -
Felix
el 14/2/17 -
Nacho
el 14/2/17 -
JUAN AMPIE
el 14/2/17Me ayudan por favor
Es de progresion aritmetica
Calcular la suma de los 33 últimos términos de la siguiente PA : ÷ (0,3) . (0,5)...... (11,3)
Antonio Silvio Palmitano
el 14/2/17Recuerda las expresiones para una progresión aritmética:
an = a1 + (n - 1)*d (para el elemento general),
Sn = (a1 + an)*n/2 (para la suma de los n elementos de la progresión),
con n ∈ N y n ≥ 1.
Tienes que el primer elemento es: a1 = 0,3, y que el segundo elemento es: a2 = 0,5, luego tienes que la diferencia es: d = a2 - a1 = 0,2, luego el elemento general queda expresado:
an = a1 + (n - 1)*d, reemplazamos valores y queda: an = 0,3 + (n - 1)*0,2, con n ∈ N, n ≥ 1.
Luego, como el último elemento es 11,3, planteamos:
an = 11,3, sustituimos y queda:
0,3 + (n - 1)*0,2 = 11,3, hacemos pasaje de término y queda:
(n - 1)*0,2 = 11, hacemos pasaje de factor como divisor y queda:
n - 1 = 55, hacemos pasaje de término y queda:
n = 56, de donde tenemos que el último elemento de la progresión tiene el número de orden 56.
Luego, observa que la suma de los últimos treinta y tres elementos de la progresión son: a24 + a25 + a26 + ... + a55 + a56
que puede expresarse como la resta entre: la suma de todos los elementos de la progresión y la suma de los primeros veintitrés elementos de la progresión.
a24 + a25 + a26 + ... + a55 + a56 = S56 - S23 (1).
Luego planteamos:
S56 = (a1 + a56)*56/2 = (0,3 + 11,3)*56/2 = 324,8,
a23 = 0,2 + (23 - 1)*0,2 = 4,6,
S23 = (a1 + a23)*23/2 = (0,3 + 4,6)*23/2 = 87,4;
luego reemplazamos en la ecuación señalada (1) y queda:
a24 + a25 + a26 + ... + a55 + a56 = S56 - S23 = 324,8 - 87,4 = 237,4.
Espero haberte ayudado.
-
Agustin Argañaraz
el 13/2/17Hola, tengo una pregunta, es sobre ecuaciones logarítmicas, y me pide que aplique la definición y/o propiedades para hallar el valor de x, y la ecuación es esta 2 log2 x + log2 1 = log2 x-1 – log5 125. ¿Como puedo hacer para resolverla? Lo único que se es que el resultado final es 1/2. Muchas Gracias.
-
Manuel Inglesias Perez
el 13/2/17 -
Alex Grattan
el 13/2/17Tengo duda sobre el ejercicio principalmente la respuesta, entiendo que se divida entre 27,ya que en principio la probabilidad de que te caiga un 1 o un 2 en un dado es 1/3,y el producto de los 3 dados nos da 1/27, pero porque 19/27,o y al vez no estoy entendiendo el ejercicio. Ayuda
