-
Fran Foce
el 13/2/17 -
Me plantean:
Dos edificios distan entre sí 90m. Desde un punto entre los dos edificios la visual a los puntos más altos de estos forman con la horizontal ángulos de 35º y 20º ¿Cuál es la altura de los dos edificios si uno es 6 metros más alto que el otro?
Mi plantamiento es el siguiente:
tag20º =h/x
tag35º=(h-6)/(90-x)
Igualo las ecuaciones y despejo h y x. Pero mi duda es sí he colocado bien los 6 metros de menos en la ecuación segunda y no debería ser en la primera.
Gracias, es un ejercicio de 4ESO
-
Como se halla la recta que pasa por el pnto de corte del plano = 3x+2y+z-3=0 con el eje ox
Alexis de Barros
el 13/2/17Antonius Benedictus
el 13/2/17 -
No estoy segura de como hacer este problema, si alguien puede ayudar seria genial puesto que tengo el examen la semana que viene...
Una fabrica produce un producto en dos calidades diferentes: x toneladas de baja calidad e y toneladas de alta calidad. Si por motivos de producción la relación entre las cantidades producidas sigue la ecuación: y=-x^4+8x^2-0,5x+9 cuantas toneladas de producto de baja calidad se han de producir para obtener ingresos máximos si el precio por tonelada de este producto es la mitad que el de alta calidad?
Antonio Silvio Palmitano
el 13/2/17Llamamos p al precio de una tonelada de producto de baja calidad, por lo que tenemos que el precio de una tonelada de producto de alta calidad es 2p.
Luego, planteamos el ingreso:
I = px + 2py, luego sustituimos la expresión para y que tenemos en el enunciado y queda:
I = px + 2p(-x4 + 8x2 - 0,5x + 9),
y observa que tenemos la expresión del ingreso en función de la cantidad de toneladas de producto de baja calidad producidas:
I(x) = px + 2p(-x4 + 8x2 - 0,5x + 9), luego planteamos la expresión de la derivada primera:
I ' (x) = p + 2p(-4x3 + 16x - 0,5),
luego planteamos la condición de punto crítico (posible máximo o posible mínimo:
I ' (x) = 0, sustituimos y queda:
p + 2p(-4x3 + 16x - 0,5) = 0, dividimos en todos los términos de la ecuación por p (observa que p es estrictamente positivo) y queda:
1 + 2(-4x3 + 16x - 0,5) = 0, distribuimos en el segundo término y queda:
1 - 8x3 + 32x - 1 = 0, cancelamos términos opuestos, extraemos factor común y queda:
- 8x(x2 - 4) = 0, hacemos pasaje de factor como divisor y queda:
x(x2 - 4) = 0, factorizamos el agrupamiento (observa que es una diferencia de cuadrados y queda:
x(x + 2)(x - 2) = 0, luego, por anulación de un producto tenemos tres opciones:
1) x = 0, que no tiene sentido para este problema;
2) x + 2 = 0, de donde despejamos: x = - 2, que no tiene sentido para este problema;
3) x - 2 = 0, de donde despejamos: x = 2,
Luego, concluimos que para que el ingreso sea máximo se deben producir 2 toneladas de producto de baja calidad.
Evaluamos para verificar la validez de la conclusión:
I(1) = 32p,
I(2) = 49p
I(3) = 0
Espero haberte ayudado.
-
∫(4/((x^2-1)^2))dx
Como se hace? Porque mira que le di vueltas.
Antonio Silvio Palmitano
el 13/2/17Vamos con una orientación: debes plantear el método de las fracciones parciales.
Observa que el denominador queda:
(x2 - 1)2 = ( (x - 1)(x + 1) )2 = (x - 1)2(x + 1)2.
Luego, planteamos para la fracción algebraica del argumento de la integral:
4 / (x2 - 1)2 = a/(x-1) + b/(x-1)2 + c/(x+1) + d/(x+1)2 = extraemos mínimo común denominasor:
= ( a(x-1)(x+1)2 + b(x+1)2 + c(x-1)2(x+1) + d(x-1)2 ) / (x - 1)2(x + 1)2.
Luego, igualamos numeradores y queda:
a(x-1)(x+1)2 + b(x+1)2 + c(x-1)2(x+1) + d(x-1)2 = 4,
luego, evaluamos para cuatro valores distintos de x, por ejemplo 1, -1, 0 y 2, y queda el sistema de ecuaciones:
4b = 4, de donde despejamos: b = 1,
4d = 4, de donde despejamos: d = 1,
- a + b + c + d = 4, reemplazamos valores y queda: - a + 1 + c + 1 = 4, hacemos pasajes de términos y queda: - a + c = 2 (1),
9a + 9b + 3c + d = 4, reemplazamos valores y queda: 9a + 9 + 3c + 1 = 4, hacemos pasajes de términos y queda: 9a + 3c = - 6 (2),
luego resuelves el sistema formado por las ecuaciones señaladas (1) (2) y tienes: a = - 1, c = 1.
Luego, la integral del enunciado queda:
I = ∫ 4 / (x2 - 1)2 dx = sustituimos = ∫ (-1/(x-1) + 1/(x-1)2 + 1/(x+1) + 1/(x+1)2) dx,
luego queda para que concluyas la tarea.
Espero haberte ayudado.
-
Una condición necesaria porque, siendo x≥0 e y≥0, se cumple que x+y=0 es que x=0 e y=0. Se tiene que demostrar y decir si es una condición suficiente.


























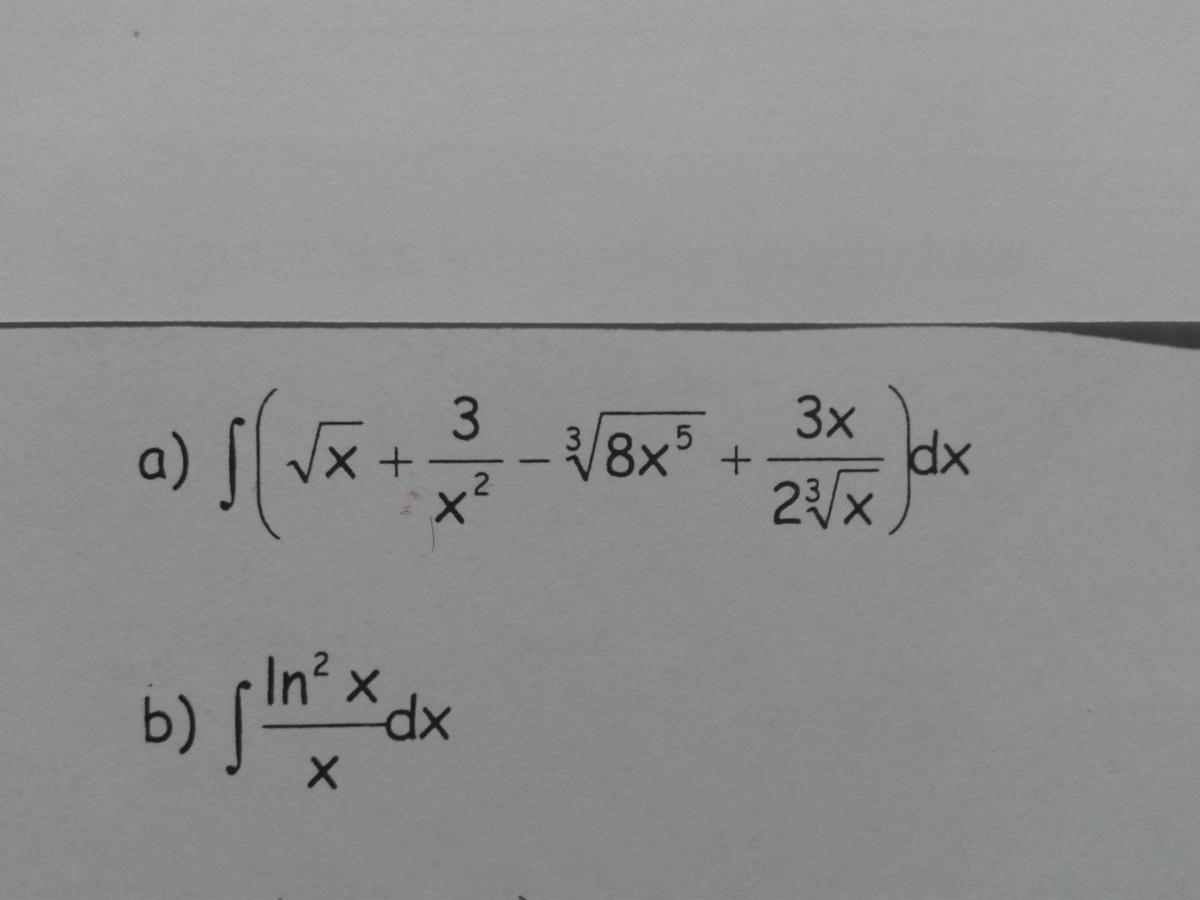 Cuando uno se bloquea, no hay manera..
Cuando uno se bloquea, no hay manera.. 


