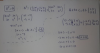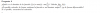-
Ulises Torres
el 13/2/17Hola, alguien seria tan amable de ayudarme a resolver esta integral; ya la intente varias veces pero no logro resolverlar. gracias. adjunto otra imagen de mi procedimiento.
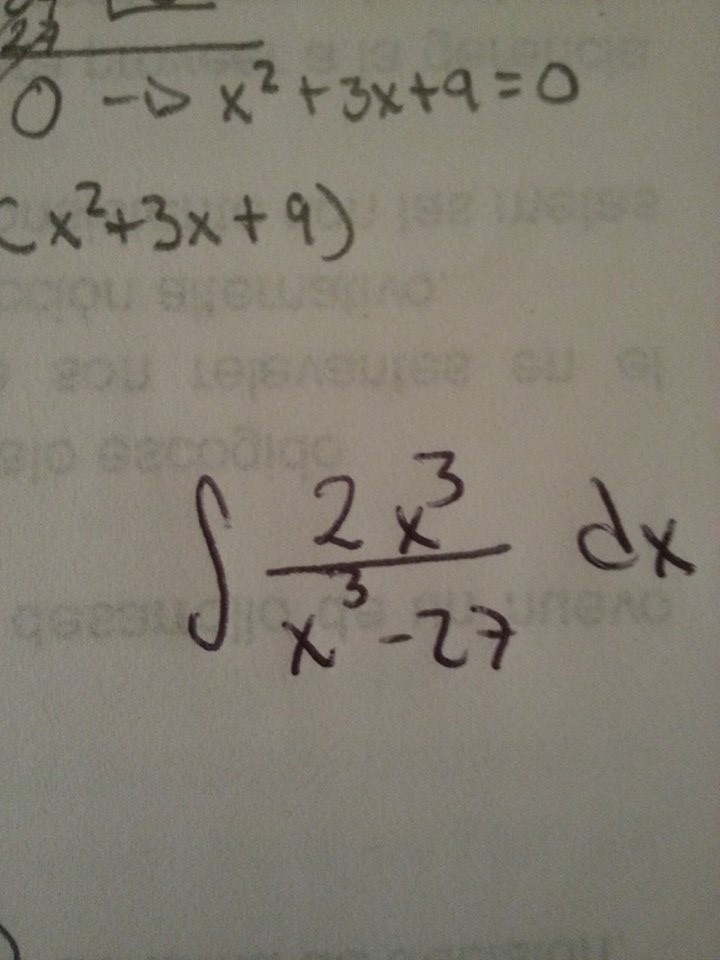
Axel Morales Piñón.
el 13/2/17 -
JUAN AMPIE
el 13/2/17
-
Jose luis Padilla
el 13/2/17 -
Carlos Ojeda
el 13/2/17Hola, ¿me echan una mano con este ejercicio de programación lineal?
Dada una máquina expendedora de bebidas calientes. Dispone de n tipos de monedas de valor a1, a2, a3, a4, , an . La máquina dispone de ui unidades del tipo ai ∀i = 1 , _,n (Valor moneda = cualquiera ) .Supón que debe devolver la cantidad C. Se pide un modelo que devuelva la cantidad C usando el menor número de monedas.
No he podido ni plantear la función objetivo ni las restricciones, estoy bloqueado.
Gracias
-
JUAN AMPIE
el 13/2/17Hola como planteo eso
Escribe un número natural que sea doce unidades menor que su cuadrado.Martin
el 13/2/17 -
Gabriel
el 13/2/17Buenas noches.Una duda con producto mixto de vectores.
Cual es la forma de operar? Porque vi dos formas distitnas, en algunos sitios vi que se calcula como A.(BxC), y en otros me sale como (AxBxC)..es decir el determinante 3x3.
Son lo mismo ambas formas?
-
Gisell Cristiano
el 13/2/17No puedo resolver este problema. Alguien me daría una idea?
Hallar los puntos (x,y) y las direcciones para las que la derivada direccional de f(x,y)=3x^2+y^2 tiene el valor máximo, si (x,y) está en el circulo x^2+y^2=1.
Antonio Silvio Palmitano
el 13/2/17Vamos con una orientación.
Observa que la función f es diferenciable en R2, por lo que tienes que el valor máximo de las derivadas direccionales evaluadas en un punto P(x,y) de su dominio es igual al módulo de su gradiente evaluado en dicho punto, por lo que tienes:
D = √(fx2 + fy2) = √( (6x)2 + (2y)2 ) = √(36x2 + 4y2),
luego, como la función D toma valores positivos, planteamos la función:
g(x,y) = D2, sustituimos y queda:
g(x,y) = 36x2 + 4y2 (observa que la función g corresponde a los valores máximos de las derivadas direccionales, elevados al cuadrado);
luego, tienes en el enunciado que los puntos P(x,y) cumplen con la restricción:
x2 + y2 = 1.
Luego, para continuar puedes aplicar el Método de los Multiplicadores de Lagrange.
Haz el intento, y si te es necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Felix
el 12/2/17
hola k tal alguien podría ayudarme con el tema 4 la (b)
Bruno Rodriguez
el 13/2/17
Antonio Silvio Palmitano
el 13/2/17Te recomiendo mires los vídeos sobre este tema, porque te serán muy útiles.
Has planteado bien los vectores normales a los planos, observa que no son paralelos, por lo que tienes que los planos son secantes y su intersección es una recta.
Para obtener las componentes de un vector director de dicha recta, planteamos el producto vectorial entre los vectores normales:
u = n1 x n2 = <-4,5,-2> x <1,7,-5> = <-11,-22,-33>.
Luego, para determinar las coordenadas de un punto de la recta, elegimos un valor para una de las coordenadas, por ejemplo z = 0, reemplazamos en las ecuaciones de los planos y queda el sistema:
-4x + 5y = 0
x + 7y +1 = 0,
luego resuelves el sistema con alguno de los métodos que has visto en clase y queda la solución: x = - 5/33, y = -4/33;
por lo que tenemos que uno de los puntos de la recta tiene coordenadas:
A(-5/33,-4/33,0).
Luego, con el vector director y el punto de la recta, planteamos las ecuaciones cartesianas paramétricas:
x = - 5/33 - 11t
y = - 4/33 - 22t
z = 0 - 33t,
con t ∈ R.
Espero haberte ayudado.
-
Javi
el 12/2/17 -
Mili Tenor
el 12/2/17Buenas tardes! Tengo un par de dudas con el tema de las ecuaciones trigonometricas.
Se que hay reglas a seguir pero solo se 3 de ellas, podrian decirme cuales son todas? muchas gracias
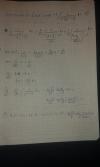
Hola me podrian ayudar con este problema por favor
