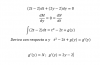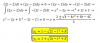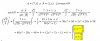-
Carmen Gomez
el 12/2/17hola, me gustaria que me explicarais como realizar las funciones
-
Iswag Newton
el 12/2/17 -
Bruno Rodriguez
el 12/2/17 -
cfdfran
el 12/2/17Buenas noches David,
necesitaba , si es posible, un video con la explicación de las progresiones cuadráticas ( 1 bachillarato ). >No las he encontrado . Solamente aparecen las aritméticas y las geométricas.
Muchisimas gracias.
Saludos
Ángel
el 14/2/17Mira desde el 04:45 hasta el final
-
Pablo Reyes
el 12/2/17 -
Sebastian Canaviiri
el 12/2/17Hola me ayudarian con el v)1 o sea yo calcule la derivada y no encontre ningun minimo pero mi profe dijo que si o si hay por una propiedad puede ser eso?
-
Paula Beatriz
el 12/2/17 -
Juan Cruz Fernandez
el 12/2/17 -
NGR2014
el 12/2/17"Dado P(x)=2x2-x-3, comprobar si es divisible por x+1 o por x-2 mediante el teorema del resto.
Comprobar a continuación efectuando la división ¿Cuál es el otro factor por el que es divisible? "
No entiendo cómo contestar la última pregunta...
-
lbp_14
el 12/2/17Hola Unicoos, si resuelvo este ejercicio de esta forma sería correcto? Si es así como podría continuar? Muchas gracias.
Antonio Silvio Palmitano
el 12/2/17Llamamos: z = x + yi al primer número complejo, y llamamos: w = u + iv al segundo número complejo.
Luego, a partir del enunciado tenemos:
z + w = 3 + i (1)
x = 2
z/w = k, con k ∈ R, de donde tenemos: z = k*w (2)
Luego sustituimos expresiones y reemplazamos x = 2 en las ecuaciones señalada (1) (2) y queda el sistema:
2 + yi + u + iv = 3 + i
2 + yi = k(u + iv)
Agrupamos términos reales e imaginarios en ambas ecuaciones y queda:
(2 + u) + (y + v)i = 3 + i
2 + yi = ku + kvi
Luego, por igualdad entre números complejos en ambas ecuaciones tenemos:
2 + u = 3, de donde despejamos: u = 1
y + v = 1
2 = ku
y = kv
Reemplazamos el valor de u remarcado en las demás ecuaciones y queda:
y + v = 1
2 = k
y = kv
Reemplazamos el valor remarcado en las demás ecuaciones y queda:
y + v = 1
y = 2v (2)
Sustituimos la expresión señalada (2) en la primera ecuación y queda:
2v + v = 1, de donde podemos despejar: v = 1/3.
Reemplazamos el valor remarcado en la ecuación señalada (2) y queda:
y = 2/3.
Luego, sobre la base de todas las ecuaciones remarcadas, concluimos que:
z = x + yi = 2 + (2/3)i;
w = u + vi = 1 + (1/3)i.
Espero haberte ayudado.
