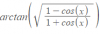Mira  bien el enunciado. Esa ecuación NO tiene x=2 por solución. Es más , es una ecuación de tercer grado cuya resolución es de matemática universitaria.

Habrá alguna errata en el libro. Gracias de nuevo!

Por cada valor de X, hay un valor y un sólo valor para Y (también llamada f(x))

Da un valor a x, y obten el valor de f(x)

Hazlo hasta que representes el rango que quieras.

Representalo en la gráfica

Si tienes más dudas, pregunta :)

(x,y)=(-1,5)+t(3,1)

Observa que x debe tomar valores positivos, y observa también que el mínimo común índice entre las raíces es 6, por lo que puedes plantear la sustitución (cambio de incógnita): x = w⁶ (1).

luego sustituyes y la ecuación queda:

∛(w⁶) = 2*√(w⁶) - 1, simplificas índices y exponentes y queda:

w² = 2*w³ - 1, haces pasajes de términos y queda:

- 2*w³ + w² + 1 = 0, multiplicas por - 1 en todos los términos de la ecuación y queda:

2*w³ - w² - 1 = 0.

Luego, observa que w₁ = 1 es una solución de la ecuación, por lo que aplicas la Regla de Ruffini:

     2    -1     0    -1

1          2     1     1

     2     1     1     0

y tienes que el polinomio del primer miembro queda factorizado, por lo que la ecuación queda::

(w - 1)*(2w² + w + 1) = 0.

Luego, por anulación de un producto, tienes dos opciones:

1)

w - 1 = 0, de donde despejas: w = 1, luego sustituyes en la ecuación remarcada y señalada (1) y tienes: x⁶ = 1, 

de donde despejas: x = ⁶√(1), de donde tenemos (recuerda que x debe tomar valores positivos): x = 1.

2)

2w² + w + 1 = 0, que es una ecuación polinómica cuadrática que puedes probar que no tiene soluciones reales.

Espero haberte ayudado.

Vas a disculpar el despiste, amiga NGR:

Gracias!

Tienes la elipse cuya ecuación puede escribirse: (2x)² + (y - 1)² = 2², luego proponemos la parametrización:

2x = 2cost

y - 1 = 2sent

con 0 ≤ t ≤ 2π;

luego, podemos despejar:

x = cost, de donde derivamos: x_t = - sent,

y = 2sent + 1, de donde derivamos: y_t = 2cost,

con 0 ≤ t ≤ 2π.

Luego, planteamos la ecuación vectorial de la trayectoria:

r(t) = < cost , 2sent + 1 >, derivamos y queda:

r ' (t) = < - sent , 2cost >,

luego planteamos la composición entre la función vectorial y el campo:

F(r(t)) = < 2sent + 1 + 3cost , 2sent + 2 - cost >;

luego planteamos:

F(r(t)) • r ' (t) = sustituimos:

= < 2sent + 1 + 3cost , 2sent + 2 - cost > • < - sent , 2cost > = desarrollamos el producto escalar:

= (2sent + 1 + 3cost)*(- sent) + (2sent + 2 - cost)*2cost = distribuimos en ambos términos:

= - 2sen²t - sent - 3sent*cost + 4sent*cost + 4cost - 2cos²t = reducimos términos semejantes, ordenamos y agrupamos términos:

= - 2(sen²t + cos²t) - sent + 4cost + sent*cost = aplicamos la identidad pitagórica en el primer término:

= - 2  - sent + 4cost + sent*cost .

Luego, planteamos el trabajo del campo vectorial:

W = ∫_C F• dr = parametrizamos:

= ∫ F(r(t)) • r ' (t) * dt (para evaluar entre 0 y 2π) = sustituimos:

= ∫ (- 2  - sent + 4cost + sent*cost)*dt = integramos (indicamos con corchetes que debemos evaluar con la Regla de Barrow entre 0 y 2π):

= [ - 2t + cost + 4sent + (1/2)sen²t ] = evaluamos:

= (- 4π + 1 + 0) - (0 + 1 + 0) = 

= - 4π + 1 - 1 = - 4π. 

Espero haberte ayudado.