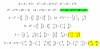-
Hola,
Por favor podrían ayudarme con esta pregunta?
No hemos visto nada de integrales elípticas, a penas vamos con integrales definidas, sólo que no sé si esto se calcula con longitud de arco o cómo se calcula, no entiendo.
Agradecería su ayuda.
Por seguridad el propietario quiere colocarle cerca eléctrica a la casa, para esto debe conocer ¿Cuántos metros lineales de cerca necesita?. Use técnicas de integración y en el caso que la integral no tenga primitiva, puede usar un software con su respectiva referencia.
Antonio Silvio Palmitano
el 29/9/19Recuerda la expresión de la longitud de arco de curva, cuya ecuación es: y = f(x), en un intervalo cerrado genérico: [a,b]:
Lab = a∫b √( 1 + f '(x)2 )*dx.
Luego, te ayudamos con las expresiones de las longitudes de arco de los nueve tramos, y observa que comenzamos desde el origen de coordenadas y recorremos el contorno con sentido antihorario, y observa también que para los tramos rectos hemos empleado consideraciones geométricas, mientras que reservamos las expresiones integrales para los demás tramos, a fin de tener la menor cantidad de cálculos posible.
1°)
Tramo parabólico:
observa que la parábola correspondiente tiene eje de simetría: y = 2, y que su vértice es V(2,-4), por lo que su ecuación canónica es:
y = (x - 2)2 + 4, con el intervalo: [0,4], y observa que la expresión de la función derivada correspondiente queda: f ' (x) = 2(x - 2) = 2x - 4;
por lo que la expresión de su longitud de arco queda:
L1 = 0∫4 √( 1 + (2x - 4)2 )*dx,
y queda que resuelvas esta integral (observa que debes aplicar una sustitución).
2°)
Tramo recto horizontal:
observa que aquí el intervalo es: [4,7], y que su longitud (que es evidente a partir de la figura) es:
L2 = 3.
3°)
Tramo recto inclinado:
observa que aquí trazas una recta vertical a partir del vértice superior (2π,4), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: (7 - 2π), y cuya altura mide: 4, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L3 = √( (7 - 2π)2 + 42 ).
4°)
Tramo senoidal:
observa que el intervalo es: [0,2π], y que la expresión de la función derivada correspondiente queda: f ' (x) = cosx;
por lo que la expresión de su longitud de arco queda:
L4 = 0∫2π √( 1 + cos2x )*dx,
y queda que resuelvas esta integral, aquí sí por medio de algún recurso informático, como sugieren en tu enunciado.
5°)
Tramo recto inclinado:
observa que aquí trazas una recta horizontal a partir del vértice izquierdo (-2,3), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: 2, y cuya altura mide: 1, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L5 = √(22 + 12) = √(4 + 1) = √(5).
6°)
Tramo recto inclinado:
observa que aquí trazas una recta vertical a partir del vértice inferior (-1,1), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: 1, y cuya altura mide: 2, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L3 = √(12 + 22) = √(1 + 4) = √(5).
7°)
Tramo recto inclinado:
observa que aquí trazas una recta vertical a partir del vértice superior (-1,1), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: 1, y cuya altura mide: 1, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L3 = √(12 + 12) = √(1 + 1) = √(2).
8°)
Tramo recto inclinado:
observa que aquí trazas una recta vertical a partir del vértice inferior (-1,-1), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: 1, y cuya altura mide: 1, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L8 = √(12 + 12) = √(1 + 1) = √(2).
9°)
Tramo recto inclinado:
observa que aquí trazas una recta vertical a partir del vértice inferior (-1,-1), y tienes un triángulo rectángulo cuya hipotenusa tiene la medida de la longitud de arco, cuya base mide: 1, y cuya altura mide: 1, por lo que aplicas el Teorema de Pitágoras, y su longitud queda expresada:
L8 = √(12 + 12) = √(1 + 1) = √(2).
Luego, tienes que la longitud del recorrido es igual a la suma de las longitudes de los nueve tramos.
Espero haberte ayudado.
-
-
Hola unicoos, tengo un problema resuelto de algebra lineal, pero no entiendo cómo hallan esa matriz transformación. ¿Alguien podría explicarme? por favor. Gracias de antemano.
-
Buenas,¿alguien me podría ayudar con este problema de probabilidad? No sé por donde cogerlo. Sé que por lo visto el computador tiene que encontrarse a uno que diga que no (2/5) y encontrar a otro que dice que si (3/4) 2/5*3/4= 0,3. El problema es que no sé porque se hace eso porque también cabría la posibilidad de que el computador se encuentre a dos que si directamente y eso no estaría recogido o al menos eso pienso. Muchas gracias de antemano

-
Hola a todos! En primer lugar, muchas gracias a José Ramos por ayudarme en los dos anteriores!! Pude corregir los q había hecho!🌷
Estuve haciendo estos ejercicios pero como aún estoy con dudas no sé si están bien. Necesito saber la respuesta para evaluar si están correctos. Si alguien puede ayudarme les estaré agradecida!!
Patri
-
Alguien puede ayudarme a plantear el ejercicio 12, se trata de programación lineal (función a maximizar sujeto a restricciones (inecuaciones)). Sólo necesito ayuda con el planteamiento, el resto del ejercicio y la gráfica lo haré por mi cuenta, muchísimas gracias
-
En un bingo, cada cartón puede ser usado para dos juegos. ¿De cuántas maneras se pueden repartir los 2 premios mayores, si hay 10 cartones en total?
La respuesta es 100,como puedo resolver eso,gracias¡
César
el 29/9/19Suponiendo que solo existen esos dos juegos tenemos:
-Primer juego: Se lo puede llevar cualquiera de los 10...
-Segundo juegos: llamemos (a) al ganador del primer juego... entonces los pares de ganadores pueden ser:
(a,a) (a, b1) (a, b2) .... (a, b9) llamando "b" a los ganadores que no sean el ganador del primer juego.
Notar entonces que por cada ganador del primer juego, existen 10 posibles dúos de ganadores (contando el caso que sea solo un ganador el que se lleva los dos premios)
Ahora como son 10 posibles ganadores del primer juego... la respuesta es 10^2 ... por lo que son 100 posibles pares de ganadores (contando la posibilidad de que gane la misma persona los dos juegos). -
-
¿De cuántas maneras pueden sentarse 7 personas alrededor de una mesa, con 7 sillas, si el abuelo de la familia ya tiene su lugar asignado?
La respuesta correcta es 720 , use la formula (N-1)! ,pero mi pregunta es ,el abuelo porque no afecta en desarrollo del ejercicio?
Antonio
el 29/9/19 -
tengo un problema que no se resolver esta ecuación.
os envió la imagen porque no es mas sencillo de visualizar. Ejercicio 4. Gracias
Antonio
el 29/9/19Usando la primera ecuación, tenemos que:
Xt+AY=B
haciendo traspuesta en ambos miembros:
(Xt+AY)t=Bt
(Xt)t+(AY)t=Bt
X+YtAt=Bt
tenemos, por tanto, el siguiente sistema:
X+YtAt=Bt
X+YtC=D
para que te sea más fácil, sustituye Yt por Z, quedando:
X+ZAt=Bt
X+ZC=D
halla las matrices traspuestas de A y B
resuelve el sistema, con lo que obtendrías las matrices X y Z
y por último, halla la matriz traspuesta de Z para obtener la matriz Y