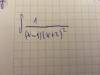-
Antonio Silvio Palmitano
el 26/1/17Puedes plantear reducción a la unidad, y observa que las magnitudes "cantidad de arroz (en Kg)" y "precio (en $)" son directamente proporcionales.
3m/p = 1/x, haces pasaje de divisores como factores y queda:
3m*x = 1*p, haces pasaje de factor como divisor y queda:
x = p/(3m), por lo que tenemos que un kilogramo de arroz cuesta $ p/(3m).
Luego, pasamos a la solución del problema:
1/x = (3/4)/y, hacemos pasajes de divisores como factores y queda:
1*y = (3/4)*x, sustituimos la expresión para x y queda:
y = (3/4)*p/(3m), simplificamos y queda:
y = p/(4m), por lo que concluimos que 3/4 kilogramos de arroz cuestan $ p/(4m), y la respuesta correcta es la opción B.
Espero haberte ayudado.
-
Hola, ¿qué tal? ¿podríais ayudarme con este sistema exponencial? No me queda nada claro... muchísimas gracias.

Antonio Silvio Palmitano
el 26/1/17Vas muy bien.
En la tercera línea de tu desarrollo has llegado a la ecuación:
20*2y - 8*4y = 8, sustituimos: 4y = (22)y = (2y)2 y queda:
20*2y - 8*(2y)2 = 8, hacemos la sustitución (cambio de incógnita): w = 2y (1), sustituimos y queda:
20*w - 8*w2 = 8, dividimos en todos los términos de la ecuación por -4 y queda:
- 5*w + 2*w2 = - 2, hacemos pasaje de término, ordenamos términos y queda:
2*w2 - 5*w + 2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
1) w = 1/2, reemplazamos en la ecuación señalada (1) y queda:
2y = 1/2, en la que tomamos logaritmos en base 2 y queda:
y = - 1, que al reemplazar en la primera ecuación del sistema del enunciado queda: x = 1;
2) w = 2, reemplazamos en la ecuación señalada (1) y queda:
2y = 2, en la que tomamos logaritmos en base 2 y queda:
y = 1, que al reemplazar en la primera ecuación del sistema del enunciado queda: x = 3.
Luego, el conjunto solución del sistema de ecuaciones queda: S = { (1,-1),(3,1) }.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 26/1/17Debes plantear el método de las fracciones parciales (observa que el segundo factor del denominador es de multiplicidad 2):
1 / (x-1)(x+2)2 = a/(x-1) + b/(x+2) + c/(x+2)2 = ( a(x+2)2 + b(x-1)(x+2) + c(x-1) ) / (x-1)(x+2)2
Luego igualamos los numeradores y queda:
a(x+2)2 + b(x-1)(x+2) + c(x-1) = 1,
que es una igualdad entre polinomios, por lo que cualquier valor real x debe verificar y, como tenemos que determinar tres coeficientes (a, b, c), elegimos tres valores, por ejemplo: x = - 2, x = 1, x = 0, y para cada uno de ellos obtenemos una ecuación, y queda el sistema:
a*0 + b*0 + c*(-3) = 1, de donde despejamos: c = -1/3,
a*9 + b*0 + c*0 = 1, de donde despejamos: a = 1/9,
a*4 + b(-1)(2) + c*(-1) = 1, reemplazamos y queda: 4/9 - 2b +1/3 = 1, de donde podemos despejar: b = -1/9.
Luego, puedes expresar a la integral del enunciado como una suma y resta de integrales:
I = (1/9)*∫ 1/(x-1) dx - (1/9)*∫ 1/(x+2) dx - (1/3)*∫ 1/(x+2)2 dx, resolvemos término a término y queda:
I = (1/9)*ln|x-1| - (1/9)*ln|x+2| + (1/3)*( 1/(x+2) ) + C.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 26/1/17Tienes un número "capicúa" con seis cifras, por lo que plantea:
"la primera cifra es igual a la sexta cifra", de donde tienes la ecuación: 3a - 1 = a + 3, haces pasajes de términos y queda: 2a = 4, de donde tienes: a = 2;
"la segunda cifra es igual a la quinta cifra", de donde tienes la ecuación: b + 1 = 4c - 7;
"la tercera cifra es igual a la cuarta cifra", de donde tienes la ecuación: c = a + 1.
Luego reemplazas el valor de a en la tercera ecuación y tienes: c = 3.
Luego reemplazas el valor de c en la segunda ecuación y tienes: b + 1 = 5, de donde tienes: b = 4.
Luego, tenemos: a + b + c = 2 + 4 + 3 = 9, por lo que concluimos que la opción B es la respuesta correcta.
Observa que el número "capicúa" de seis cifras es: N 0 553355.
Espero haberte ayudado.
-
Antonius Benedictus
el 26/1/17Antonio Silvio Palmitano
el 26/1/17Llamemos: u = x2 + x, cuya derivada queda: u ' = 2x + 1,
observa que para x = 0 tenemos: u = 02 + 0 = 0, u ' = 2(0) + 1 = 1.
Luego, observa que la ecuación implícita del enunciado puede escribirse:
f( g(u) ) + 3g(x) = 3ln(x +1) + 1 (1);
luego derivamos (observa que tenemos que aplicar la regla de la cadena en el primer término del primer miembro y queda:
f ' ( g(u) )*g ' (u)*u ' + 3g ' (x) = 3/(x + 1).
Luego, evaluamos para x = 0 (recuerda que corresponde también u = 0 y u ' = 0, reemplazamos y queda:
f ' ( g(0) )*g ' (0)*1 + 3g ' (0) = 3/(0 + 1).
Luego reemplazamos g(0) = 0 y g ' (0) = - 2 que tenemos en el enunciado y queda:
f ' ( 0 )*(-2)*1 + 3(-2) = 3, resolvemos factores numéricos y queda:
-2f ' (0) - 6 = 3, hacemos pasaje de término y queda:
-2f ' (0) = 9, hacemos pasaje de factor como divisor y queda:
1) f ' (0) = - 9/2.
2) Observa que planteamos para la recta normal en el punto de abscisa x = 0:
a) ordenada: y = f(0): evaluamos la expresión señalada (1) = f( g(0) ) + 3g(0) = 3ln(0 + 1) + 1,
reemplazamos los valores conocidos y queda: f( 0 ) + 3(0) = 2ln(1) + 1,
resolvemos términos y queda: f ( 0 ) = 1, por lo que el punto de contacto entre la recta normal y la gráfica de la función f tiene coordenadas: A(0,1);
b) pendiente: a partir de la relación entre la derivada y la recta normal, planteamos:
m = - 1 / f ' (0), reemplazamos el valor de la derivada que hemos remarcado y queda: m = 2/9;
c) planteamos la ecuación de la recta normal a la gráfica dela función en el punto de abscisa x = 0:
y - 1 = (2/9)(x - 0), que en forma explícita queda: y = (2/9)x + 1.
Espero haberte ayudado.
-
Hola Unicoos, ¿me podríais ayudar con la resolución de este ejercicio de geometría de 2 bachillerato?
Hallar la ecuación del plano que pasa por el punto P(1,2,3), siendo equilátero el triángulo formado por los puntos en los que dicho plano corta a los ejes cartesianos. Calcular el volumen determinado por dicho triángulo equilátero y el origen de coordenadas.
-
Analiza la siguiente falacia:
Un compañero de trabajo en una oficina dice a otro: ''Sólo diré que me parece extraño que seas tú el que dé esos argumentos en contra del plan propuesto. Hace unos años eras tú quien lo defendía con una tenacidad que no dejaba de asombrarnos.''
Ángel
el 26/1/17Claramente una "falacia ad hominem" (dirigida contra el hombre) :D :D
-En vez de presentar razones adecuadas para rebatir una posición/conclusión, se ataca/desacredita a la persona que la defiende
**Formalización lógica implícita:
A afirma P
A no es una persona digna de crédito
|- por lo tanto, no P