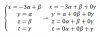-
Ángel
el 28/1/17Suponiendo que solo existen esos dos juegos tenemos:
-Primer juego: Se lo puede llevar cualquiera de los 10
-Segundo juego: llamemos (a) al ganador del primer juego; entonces los pares de ganadores pueden ser:
(a,a) (a, b1) (a, b2) .... (a, b9), llamando "b" a los ganadores que no sean el ganador del primer juego.
Observa que entonces por cada ganador del primer juego, existen 10 posibles dúos de ganadores(contando el caso que sea solo un ganador el que se lleva los dos premios)
Como son 10 posibles ganadores del primer juego, la respuesta es 102 ... por lo que son 100 posibles pares de ganadores (contando la posibilidad de que gane la misma persona los dos juegos)
LA RESPUESTA CORRECTA ES LA E)
-
------------------------------------------------------------------------Geografía y Trigonometría------------------------------------------------------------------------
-
Antonio Silvio Palmitano
el 27/1/17Vamos con una orientación.
Observa que todas las proposiciones son condicionales: p → q,
que en palabras se enuncia, generalmente: "Si p entonces q" (observa que en el lenguaje coloquial a veces se omite la palabra "entonces"),
por lo que tenemos que le antecedente p es la hipótesis, y el consecuente q es la tesis.
Haz el intento de identificar hipótesis y tesis en cada enunciado, y si te es preciso, no dudes en volver a consultar.
Espero haberte ayudado.
Matemáticas
el 27/1/17(a) Hipótesis: el triángulo rectángulo ABC, de catetos a, b y hipotenusa c, tiene el área igual a (1/a)c². / Tesis: El triángulo ABC es isósceles.
(b) Hipótesis: n es un entero par. / Tesis: n² también es par.
(c) Hipótesis: Sean a, b, c, d, e, f seis nombres reales que ad-bc (distinto) de 0. / Tesis: El sistema de ecuaciones lineales tiene una solución en x, e y.
(d) Hipótesis: La suma de los n primeros números naturales. /Tesis: es (1/2)n(n+1).
(e) Hipótesis: Si r es un número real y r²=2. / Tesis: r no puede ser racional.
(f) Hipótesis: p, q son dos números reales positivos con la expresión del enunciado. / Tesis: p distinto de q.
(g) Hipótesis: x es un número real. / Tesis: el valor de x(x-1) es al menos -1/4.
Seria así Antonio o hay algun error?
-
Antonio Silvio Palmitano
el 27/1/17Observa que te faltaron sumar 15 mm del mes de abril, por lo que la ecuación del promedio queda:
( 240 + (x + y) )/12 = 25, haces pasaje de divisor como factor y queda:
240 + (x + y) = 300, haces pasaje de término y queda:
x + y = 60.
Por lo que tenemos que a opción A es la respuesta correcta: llovieron 60 mm en total entre los meses de octubre y noviembre.
Espero haberte ayudado.
-
¡Hola! ¿Cómo se haría este ejercicio?
Sean los vectores u y v tales que u·(u+v)-(u-v)·v = 31 y |u+v|2 = 37. Halla el producto escalar de u·v.
¡Gracias!
Antonio Silvio Palmitano
el 27/1/17Distribuimos en la primera ecuación y queda (indicamos producto escalar con *):
u*u + u*v- u*v + v*v = 31,
cancelamos términos opuestos, aplicamos la propiedad del producto escalar de un vector por si mismo que es igual a su módulo elevado al cuadrado y queda:
|u|2 + |v|2 = 33 (1).
En la segunda ecuación, aplicamos la propiedad del producto escalar de un vector por si mismo que es igual a su módulo elevado al cuadrado y queda:
(u + v)*(u + v) = 37, distribuimos y queda:
u*u + u*v + v*u + v*v = 37, reducimos términos semejantes (recuerda que el producto escalar es conmutativo) y queda:
u*u + 2u*v + v*v = 37,
aplicamos la propiedad del producto escalar de un vector por si mismo que es igual a su módulo elevado al cuadrado y queda:
|u|2 + 2u*v + |v|2 = 37 (2).
Luego, con las ecuaciones señaladas (1) (2) tenemos el sistema:
u|2 + |v|2 = 33
|u|2 + 2u*v + |v|2 = 37
restamos miembro a miembro (observa que tenemos cancelaciones) y queda:
- 2u*v = - 4, hacemos pasaje de factor como divisor y llegamos a:
u*v = 2.
Espero haberte ayudado.
-
 Hola unicoos, me podrían decir si las siguientes demostraciones están concluidas finalmente, o le falta algo para finalizar la demostración...
Hola unicoos, me podrían decir si las siguientes demostraciones están concluidas finalmente, o le falta algo para finalizar la demostración...David
el 1/2/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
De las expresiones matemáticas siguientes, cuáles son ciertas, cuáles son falsas y cuáles son ambiguas.
(a) La raíz cuadrada de un entero es un número real no negativo.
(b) Hay un ángulo α que sen α = cos α.
(c) x < 1.
(d) Si x < 1, entonces x^(2) <1.
(e) Si x es un número complejo arbitrario, entonces x^(2)-x = 1.
Ambiguo quiere decir que su valideza o falsedad dependen del valor que tengan las variables x e y.
Antonius Benedictus
el 27/1/17Guillem De La Calle Vicente
el 27/1/17 -
------------------Geometría y Trigonometría------------------
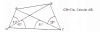
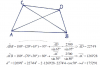
15) Determinar los lados y el área de un paralelogramo con los siguientes datos: la diagonal mayor es de 20m y forma con los lados ángulos de 30°22' y 26°18'
-
Si por ejemplo, tengo este subespacio de R4 . S= (x,y,z,t) E R4: x + 3y=z
¿Como determino un sistema generador con este subespacio? ¡Muchas gracias!
Ylenia Montes
el 27/1/17Antonius Benedictus
el 27/1/17Antonio Silvio Palmitano
el 27/1/17Una manera alternativa para ver los elementos de la base del subespacio S:
a partir de la condición que cumplen las componentes de un vector del subespacioS, puedes despejar: x = - 3y + z (1).
Luego, tomamos un vector genérico perteneciente a S:
u = < x , y , z , t > = sustituimos la primera componente por la expresión señalada (1) y queda:
= < - 3y + z , y , z , t > = descomponemos como suma, con una indeterminada en cada término y queda:
= < - 3y , y , 0 , 0 > + < z , 0 , z , 0 > + < 0 , 0 , 0 , t > = extraemos factores escalares en los términos y queda:
= x * < -3 , 1 , 0 , 0 > + z*< 1 , 0 , 1 , 0 > + t*< 0 ,0 , 0 , 1 >.
Luego, tenemos que el vector genérico perteneciente al subespacio S es una combinación lineal de los vectores del conjunto:
A = { < -3 , 1 , 0 , 0 > , < 1 , 0 , 1 , 0 > , < 0 ,0 , 0 , 1 > };
por lo que tenemos que el conjunto A es un conjunto generador del subespacio S.
Luego, puedes demostrar que los vectores pertenecientes al conjunto a son linealmente independientes, y puedes concluir que el conjunto A es una base del subespacio S.
Espero haberte ayudado.
Antonius Benedictus
el 27/1/17