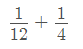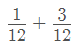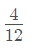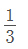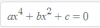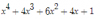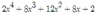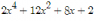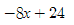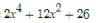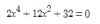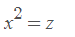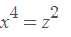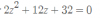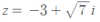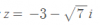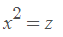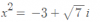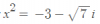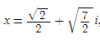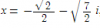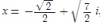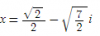-
OTRA PREGUNTA:
EL AGUA DE UNA FUENTE PUEDE LLENAR EL DEPÓSITO DE AGUA EN 12 DÍAS Y LA DE OTRA FUENTE EN 4 DÍAS. ¿CUÁNTO TARDARÁN EN LLENARLO LAS DOS FUENTES JUNTAS?
A. A. 8 días.
B. B.3 días.
C. 2,66 días.Breaking Vlad
el 23/9/19Jose Ángel
el 23/9/19Clow
el 23/9/19Tu planteo es incorrecto, para darse cuenta hay que leer los ejercicios con sentido común antes que intentar plantear los cálculos. Si la segunda fuente llena el depósito en 4 días, no hay manera de que las dos fuentes juntas demoren más de 4 días, deben demorar menos de eso.
La primera fuente tarda 12 días en llenar el depósito, así que por día llena
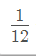 de su capacidad. La otra tarda 4 días, así que por día llena
de su capacidad. La otra tarda 4 días, así que por día llena 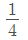 de la capacidad.
de la capacidad.Si son las dos juntas, llenaran por día la suma de esos valores:
Una vez efectuada la operación, el resultado es un tercio. O sea que por día, las dos fuentes juntas llenan un tercio del depósito, con lo que tardarán tres días en llenarlo completamente. La respuesta es la B.
Antonio Silvio Palmitano
el 23/9/19Puedes llamar V al volumen del depósito, y luego tienes que los caudales (Q = V/t) aportados por cada una de las fuentes quedan expresados:
Q1 = V/12,
Q2 = V/4,
ambas expresadas en (unidad de volumen)/día.
Luego, planteas la expresión del caudal total aportado por las dos fuentes en forma simultánea, y queda:
Q = Q1 + Q2, sustituyes expresiones, y queda:
Q = V/12 + V/4, extraes denominador común, y queda:
Q = (V + 3V)/12, resuelves el numerador, y queda:
Q = 4V/12, simplificas, y queda:
Q = V/3, expresado en (unidad de volumen)/día.
Luego, planteas la expresión del caudal total en función del volumen del depósito y del tiempo, y queda:
Q = V/t, sustituyes la expresión del caudal que tienes remarcada, y queda:
V/3 = V/t, multiplicas por t, multiplicas por 3 y divides por V en ambos miembros, y queda:
t = 3 días,
por lo que puedes concluir que la opción señalada (B) es la respuesta correcta, como te indica el colega Clow.
Espero haberte ayudado.
-
SABIENDO QUE UN DEPÓSITO DE AGUA TIENE FORMA DE PRISMA DE 6 M DE LARGO POR 5 M DE ANCHURA, ¿QUÉ ALTURA ALCANZARÁ EL AGUA EN SU INTERIOR CUANDO CONTENGA 75.000 LITROS?
OPCIONES:
A. A. 2,25 m
B. 0,78 m
C. 2,50 m
GRACIAS.
Breaking Vlad
el 23/9/19Jose Ángel
el 23/9/19Antonio Silvio Palmitano
el 23/9/19Tienes las dimensiones del tanque prismático rectangular:
L = 6 m,
A = 5 m,
H = a determinar (en m),
por lo que la expresión de su volumen queda:
V = L*A*H, reemplazas valores, y queda:
V = 6*5*H, resuelves la multiplicación numérica, y queda:
V = 30*H (en m3).
Luego, tienes el valor del volumen:
V = 75000 L = 75000 dm3 = 75000/1000 = 75 m3;
luego, reemplazas este valor en la ecuación remarcada, y queda:
75 = 30*H, y de aquí despejas:
H = 75/30, resuelves, y queda:
H = 2,5 m,
por lo que has concluido correctamente que la opción señalada (C) es la respuesta correcta.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 23/9/19Vamos con tres propuestas:
a)
h(x) = x (1),
que es la expresión de una función continua en el intervalo [-3,3].
b)
Aquí puedes dividir a la expresión señalada (1) por (x - 1) y por (x - 2), observa que estas expresiones toman el valor cero para x = 1 y para x = 2, respectivamente, y queda:
f(x) = x/( (x - 1)*(x - 2) ),
que es la expresión de una función que presenta discontinuidades esenciales en x = 1 y x = 2.
c)
Aquí multiplicas y divides a la expresión señalada (1) por (x + 2), observa que esta expresión toma el valor cero para x = -2, y queda:
g(x) = x(x + 2)/(x + 2),
que es la expresión de una función que presenta discontinuidad evitable en x = -2.
Espero haberte ayudado.
-
Hola, no se me ocurre como hacer esto, alguna idea?:
Hallar todos a,b∈N tales que mcd(a,b) = 12, a tiene 15 divisores positivos y b tiene 12
Mathias
el 22/9/19Mathias
el 23/9/19 -
Holaaa, alguien me puede explicar esta ecuación bicuadrada?
2(x+1)^4-8x^3-8(x-3)+6=0
Clow
el 22/9/19Las ecuaciones bicuadradas tienen la forma
Entonces debes desarrollar la expresión que tienes para escribirla de esa manera.
Si desarrollas el (x+1)^4, tendrás:
Eso está multiplicado por 2, así que:
Si te fijas, quedó un 8x^3, pero en tu expresión luego se resta 8x^3, así que, como se esperaba, pierdes el término al cubo, te queda:
Ahora, en la expresión inicial sigue un -8(x-3), lo desarrollas:
Verás que tienes el -8x restando, y en la parte anterior hay un 8x, así que se anula el término de grado 1, quedando:
A eso falta sumar el 6, así que finalmente la ecuación bicuadrada queda:
Para resolverla cambiarás tu variable de forma que:
Reescribes:
Ahora tienes una ecuación de segundo grado que se resuelve con fórmula cuadrática. Cuando operes verás que obtienes dos raíces imaginarias:
Ahora, retomamos que
Y sustituyes por los valores de z hallados:
Despejas la x pasando el cuadrado como raíz cuadrada, así que habrá dos soluciones por cada una, en total cuatro soluciones (porque trabajas con una ecuación de grado 4):
-
Es decir, si tengo por ejemplo:
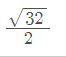
¿Cómo simplifico eso para que me quede solamente la raíz de un número?
Jose
el 22/9/19Antonio Silvio Palmitano
el 22/9/19Tienes la expresión numérica:
√(32)/2 =
expresas el argumento de la raíz cuadrada como el producto de un cuadrado perfecto máximo por un número, y queda:
= √(16*2)/2 =
distribuyes la raíz en el numerador, y queda:
= √(16)*√(2)/2 =
resuelves el primer factor en el numerador (consideramos la raíz cuadrada positiva), y queda:
= 4*√(2)/2 =
simplificas, y queda:
= 2*√(2) =
expresas al primer factor como la raíz cuadrada de su cuadrado, y queda:
= √(4)*√(2) =
asocias las raíces cuadradas, y queda:
= √(4*2) =
resuelves el argumento de la raíz cuadrada, y queda:
= √(8).
Espero haberte ayudado.
-
-
https://www.unicoos.com/discusion/215015#
Subo el ejercicio que planteé para ver si hay algún error. Saludos.
Antonio Silvio Palmitano
el 22/9/19Debes tener en cuenta que la forma que empleas para expresar los resultados no es correcta, con respecto a la notación.
Luego, vamos con las respuestas que debes corregir:
e)
Lím(x→∞) ( f(x) )-x = Lím(x→∞) 1/( f(x) )x = 0, ya que el numerador es constante y el denominador tiende a infinito.
f)
Lím(x→∞) u(x)f(x) es indeterminado, ya que la base de la potencia tiende a cero y el exponente tiende a infinito.
k)
Lím(x→∞) ( f(x) )h(x) = Lím(x→∞) 1/( f(x) )-h(x) = 0, ya que el numerador es constante y el denominador tiende a infinito.
l)
Lím(x→∞) ( h(x) )h(x) = Lím(x→∞) 1/( h(x) )-h(x) = 0, ya que el numerador es constante y el denominador tiende a ±infinito.
m)
Lím(x→∞) ( -h(x) )h(x) = Lím(x→∞) 1/( -h(x) )-h(x) = 0, ya que el numerador es constante y el denominador tiende a infinito.
o)
Lím(x→∞) h(x)/u(x) = -∞, ya que el numerador tiende a -infinito y el denominador tiende a una constante positiva.
p)
Lím(x→∞) x-x = Lím(x→∞) 1/xx = 0, y que el numerador es constante y el denominador tiende a infinito.
Espero haberte ayudado.