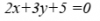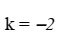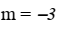-
Hola unicoos necesito su gran ayuda, eh tratado de resolver los ejercicios pero nunca puedo llegar a la respuesta correcta, no se si la resolución del práctico estará mal hecho, abajo les dejaré el problema y al lado la respuesta, bueno eso es todo gracias.
Antonio Silvio Palmitano
el 20/9/19c)
Despejas y en la ecuación de la recta de referencia, y queda:
y = (3/2)x + 5/2, que es la ecuación cartesiana explícita, y observa que la recta de referencia tiene pendiente: 3/2.
Luego, recuerda la condición de perpendicularidad, por lo que tienes que la recta buscada tiene pendiente contraria y recíproca, por lo que puedes plantear que su valor es: m = -2/3;
luego, como tienes que el punto (2,-3) pertenece a la recta buscada, planteas la ecuación punto-pendiente, y queda:
y = -(2/3)*(x - 2) - 3, distribuyes el segundo término, y queda:
y = -(2/3)*x + 4/3 - 3, multiplicas por 3 en todos los términos, y queda:
3*y = -2*x + 4 - 9, reduces términos numéricos, y queda:
3*y = -2*x - 5, sumas 2*x y sumas 5 en ambos miembros, y queda:
2*x + 3*y + 5 = 0.
8)
Observa que k indica el valor de la pendiente de la recta buscada, de la que tienes planteada su ecuación cartesiana explícita;
luego, multiplicas por -2 en todos los términos de la ecuación de la recta de referencia, y queda:
2*x + y = -2, restas 2*x en ambos miembros, y queda:
y = -2*x - 2, por lo que tienes que -2 es la pendiente de la recta de referencia.
Luego, recuerda la condición de paralelismo, por lo que tienes que la recta buscada tiene la misma pendiente que la recta de referencia, por lo que puedes plantear que su valor es: k = -2;
luego, reemplazas este valor en la ecuación de la recta buscada que tienes en tu enunciado, y queda:
y = -2*x - 1.
9)
Despejas y en la ecuación de la recta buscada, y queda:
y = m*x + 4, que es su ecuación cartesiana explícita, en la que tienes planteado que su pendiente es: m;
luego, despejas y en la ecuación de la recta de referencia, y queda:
y = (1/3)*x, y observa que su pendiente es (1/3), y por la condición de perpendicularidad que ya hemos presentado en el primer ejercicio, tienes que la pendiente de la recta buscada es: m = -3;
luego, reemplazas este valor en la ecuación de la recta buscada que tienes en tu enunciado, y queda:
-3*x - y + 4 = 0.
Espero haberte ayudado.
-
Antonio
el 19/9/19Antonio Silvio Palmitano
el 19/9/19Vamos con una orientación.
Tienes la ecuación trascendente:
x2 = 8*lnx, restas 8*lnx en ambos miembros, y queda:
x2 - 8*lnx = 0 (1).
Luego, observa que en el primer miembro de la ecuación señalada (1) tienes la expresión de una función:
f(x) = x2 - 8*lnx, que es continua y también derivable en el intervalo que indican en tu enunciado: I = (0, e],
cuya función derivada tiene la expresión:
f'(x) = 2*x - 8/x (2).
Luego, planteas la condición de punto estacionario (posible máximo o posible mínimo de la función), y queda:
f'(x) = 0, sustituyes la expresión señalada (2) en el primer miembro, y queda:
2*x - 8/x = 0, multiplicas por x (observa que x toma valores distintos de cero en el intervalo) y divides por 2 en ambos miembros, y queda:
x2 = 4, extraes raíz cuadrada en ambos miembros, y tienes dos opciones:
1°)
x = -2, que no pertenece al intervalo I = (0, e], por lo que no tiene sentido para este problema;
2°)
x = 2, que sí pertenece al intervalo I = (0, e], por lo que sí tiene sentido para este problema,
y observa que en este punto la función toma el valor: f(2) = 4 - 8*ln(2) ≅ -1,545, y observa que este valor es negativo.
Luego, derivas la expresión señalada (2), y la expresión de la función derivada segunda queda:
f''(x) = 2 + 8/x2 (3);
luego, observa que la expresión señalada (3) toma valores positivos en todo el intervalo, por lo que tienes que la gráfica de la función es cóncava hacia arriba en todo el intervalo, por lo que tienes que la gráfica de la función presenta un mínimo en el punto: A( 2 ; 4 - 8*ln(2) ), por lo que tienes además que la función es decreciente en el subintervalo: I1 = (0,2), y es creciente en el subintervalo: I2 = (2,e].
Luego, considera el subintervalo: I1 = (0,2), y observa que la función es decreciente en este subintervalo.
Planteas el límite de la función para x tendiendo a cero por la derecha, y queda:
Lím(x→0+) (x2 - 8*lnx) = +∞,
por lo que tienes que la función toma valores positivos para x muy cercano a cero, pero toma un valor negativo en el punto estacionario (x = 2), por lo que tienes que corta una sola vez al eje OX en este subintervalo, y puedes concluir que existe un valor c perteneciente al subintervalo I1 = (0,2), en el cuál la función toma el valor cero, por lo que puedes plantear la ecuación:
f(c) = 0, sustituyes la expresión evaluada de la función en el primer miembro, y queda:
c2 - 8*ln(c) = 0, sumas 8*ln(c) en ambos miembros, y queda:
c2 = 8*ln(c), por lo que tienes que x = c es una solución de la ecuación de tu enunciado.
Luego, considera el subintervalo: I2 = (2,e], y observa que la función es creciente en este subintervalo.
Evalúas la expresión de la función para el extremo derecho del intervalo, y queda:
f(e) = e2 - 8*ln(e) ≅ -0,611,
que es un valor negativo mayor que el valor de la función en el punto estacionario (recuerda: f(2) ≅ -1,545), por lo que tienes que la gráfica de la función no corta al eje OX en el subintervalo: I2 = (2,e], por lo que la función toma valores negativos en este subintervalo y, por lo tanto, la función no toma el valor cero para algún elemento de él y no existe valor alguno que sea solución de la ecuación de tu enunciado.
Luego, puedes concluir que existe un único valor x = c, perteneciente al subintervalo: I1 = (0,2) que es solución de la ecuación de tu enunciado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 20/9/19Vamos con una orientación.
Tienes la ecuación:
p + 1/(q + 1/r) = 25/19,
resuelves el denominador del segundo término, sumas y restas uno en el segundo miembro, y queda:
p + 1/( (q*r + 1)/r ) = 1 - 1 + 25/19,
resuelves la división entre expresiones fraccionarias en el segundo término, reduces los dos últimos términos en el segundo miembro, y queda:
p + r/(q*r + 1) = 1 + 6/19 (1).
Luego, observa que los cuatro términos de la ecuación señalada (1) son positivos, observa que el denominador del segundo término es mayor que su numerador, por lo que puedes plantear las ecuaciones:
p = 1,
r/(q*r + 1) = 6/19, multiplicas por 19 y multiplicas por (q*r + 1) en ambos miembros, y queda:
19*r = 6*(q*r + 1) (2);
luego, observa que los factores 6 y 19 no tienen divisores comunes excepto el uno (o sea: son coprimos), por lo que tienes que el factor r debe ser un múltiplo de 6, y el factor (q*r + 1) debe ser un múltiplo de 25, observa que para que se verifique la igualdad puedes plantear las ecuaciones:
r = 6*x (3),
q*r + 1 = 19*x (4);
luego, sustituyes la expresión señalada (3) en el primer término de la ecuación señalada (2), y queda:
q*6*x + 1 = 19*x;
restas 19*x y restas 1 en ambos miembros, y queda:
q*6*x - 19*x = -1,
extraes factor común (-x) en el primer miembro, y queda:
-x*(-q*6 + 19) = -1,
multiplicas por -1 en ambos miembros, y queda:
x*(-q*6 + 19) = 1 (5),
y observa que para que se verifique la ecuación señalada (5) tienes que los dos factores del primer miembro deben ser iguales a uno, entonces tienes que debe cumplirse:
x = 1, reemplazas este valor en la ecuación señalada (3), resuelves, y queda: r = 6,
-q*6 + 19 = 1, y de aquí despejas: q*6 = 18, y luego despejas: q = 3.
Luego, planteas la expresión cuyo valor te piden en tu enunciado, y queda:
p*q*r = reemplazas los valores remarcados = 1*3*6 = 18.
Espero haberte ayudado.
-
Hola a todos, alguien me explicaría brevemente este ejercicio?? Me pide que halle el plano que contiene al eje de abscisas y es perpendicular al vector normal (0,-3,1). que contenga al eje x quiere decir que cualquier punto de ese eje pertenece al plano y un vector normal no seria de la forma (x,0,0) ??? Gracias
Laura
el 20/9/19 -
Al resolver dicho ejercicio calculando el RANGO DE LA MATRIZ con el vector director de r, el vector director de s y el vector director de los puntos de ambas rectas, el resultado es que la MATRIZ A*, tiene un RANGO=3 , y por tanto según la teoria, dichas rectas SE CRUZAN.
Mi respuesta por tanto sería la D, pero en la plantilla de corrección la respuesta es la B.
Jose Ramos
el 19/9/19CUIDADO con el numerador de la expresión continua de z en la recta s. El vector director de s es (2, 1, -3) y el punto de s es (0,2,2). Con esos datos a mi me da Rango de A* = 2, con lo cual las rectas se cortan en un punto. La respuesta correcta sería la B. (Es una puñetita que a veces puede surgir, así que cuidado con las ecuaciones continuas)
-
¿la altura y peso de una persona no tiene una relación directa? En general a mayor altura mayor peso ¿no?
Clow
el 19/9/19