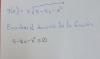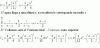-
Buenos dias Unicoos, he tratado de realizar este ejercicio pero no encuentro la manera. Me podrian ayudar por favor.
Antonio Silvio Palmitano
el 19/9/19Vamos con la condición que indica el colega Clow en su respuesta a tu consulta anterior:
8 - 8x - x2 ≥ 0, multiplicas por -1 en todos los términos de esta inecuación (observa que cambia la desigualdad), y queda:
-8 + 8x + x2 ≤ 0, sumas 8 en ambos miembros, ordenas términos en el primer miembro, y queda:
x2 + 8x ≤ 8, sumas 16 en ambos miembros, y queda:
x2 + 8x + 16 ≤ 24, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x + 4)2 ≤ 24, extraes raíz cuadrada positiva en ambos miembros, y queda:
|x + 4| ≤ √(24), extraes factores racionales de la raíz cuadrada, y queda:
|x + 4| ≤ 2√(6), expresas esta inecuación como una inecuación doble, y queda:
-2√(6) ≤ x + 4 ≤ 2√(6), restas 4 en los tres miembros de esta inecuación doble, y queda:
-4 - 2√(6) ≤ x ≤ -4 + 2√(6), que es la condición que deben satisfacer los elementos del dominio de la función;
luego, expresas al dominio de la función como intervalo cerrado, y queda:
Dg = [ -4 - 2√(6) ; -4 + 2√(6) ].
Espero haberte ayudado.
Clow
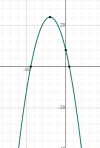
el 19/9/19Otra manera más sencilla es hallando las raíces de la expresión y graficándola.
Las raíces se encuentran con fórmula cuadrática, y serán:
x=-2(2+√6)
x,=2(√6-2)
Ahora, sabemos que es una función de segundo grado, una parábola, y como el coeficiente del x^2 es negativo (-1), significa que la concavidad es hacia abajo. Esbozas eso y verás que los valores positivos son los comprendidos en el intervalo entre esas dos raíces, y como también nos sirve que el resultado sea cero, lo escribes con paréntesis recto para incluir los valores de las raíces en el dominio.
D(g)= [ -4 - 2√(6) ; -4 + 2√(6) ]
-
Clow
el 19/9/19Para determinar el dominio de una función, debes ver para qué valores de x existe una imagen. En este caso tienes una raíz, y el problema que puede presentarte es si dentro de ella queda un valor negativo, puesto que no puedes hacer la raíz de un número negativo.
Lo que debes hacer es plantear la inecuación
8-8x-x^2≥0
Es una inecuación cuadrática. En estos casos primero te fijas si puedes factorizar la expresión. Pero se trabaja con los puntos críticos, o sea, las raíces. Lo haces con fórmula cuadrática y te fijas que satisfaga la desigualdad.
Antonio Silvio Palmitano
el 19/9/19Vamos con la condición que indica el colega Clow:
8 - 8x - x2 ≥ 0, multiplicas por -1 en todos los términos de esta inecuación (observa que cambia la desigualdad), y queda:
-8 + 8x + x2 ≤ 0, sumas 8 en ambos miembros, ordenas términos en el primer miembro, y queda:
x2 + 8x ≤ 8, sumas 16 en ambos miembros, y queda:
x2 + 8x + 16 ≤ 24, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(x + 4)2 ≤ 24, extraes raíz cuadrada positiva en ambos miembros, y queda:
|x + 4| ≤ √(24), extraes factores racionales de la raíz cuadrada, y queda:
|x + 4| ≤ 2√(6), expresas esta inecuación como una inecuación doble, y queda:
-2√(6) ≤ x + 4 ≤ 2√(6), restas 4 en los tres miembros de esta inecuación doble, y queda:
-4 - 2√(6) ≤ x ≤ -4 + 2√(6), que es la condición que deben satisfacer los elementos del dominio de la función;
luego, expresas al dominio de la función como intervalo cerrado, y queda:
Dg = [ -4 - 2√(6) ; -4 + 2√(6) ].
Espero haberte ayudado.
-
Hola unicoos quería saber cómo puedo resolver el ejercicio que les dejo abajo, es todo gracias.
Encuentra la ecuación de la recta que:
a) pasa por (2; –3) y es perpendicular a 3x – 2 y + 5 = 0
Clow
el 19/9/19En el apartado a, primero determinas la pendiente de la recta dada, reescribiéndola con la forma y=ax+b. Al hacerlo verás que la pendiente (a), es 3/2. Para que sean rectas perpendiculares el producto de las pendientes debe ser -1, o sea que son inversas y opuestas. Por lo que la pendiente de la recta que quieres encontrar es -2/3. Ahora utilizando el punto que te dan, sustituyes en y=ax+b (sustituyes la x e y del punto y el a por la pendiente -2/3). Despejas la b, que será -5/3 y la respuesta es:
y=-2/3-5/3
Antonio Silvio Palmitano
el 19/9/19a)
Observa que tienes la ecuación cartesiana implícita de la recta de referencia:
3x - 2y + 5 = 0,
por lo que puedes proponer que los coeficientes principales son iguales en la ecuación cartesiana implícita de la recta buscada, por lo que puedes plantear que su ecuación es:
3x - 2y + C = 0 (1);
luego, reemplazas las coordenadas del punto (2,-3) que debe pertenecer a la recta, y queda:
3(2) - 2(-3) + C = 0, y de aquí despejas: C = -12;
luego, reemplazas este valor en la ecuación de la recta buscada señalada (1), y queda:
3x - 2y + (-12) = 0,
resuelves signos en el tercer término, y queda:
3x - 2y - 12 = 0.
b)
Observa que tienes la ecuación continua (o segmentaria) de la recta de referencia:
x/(-2) + y/(-1) = 1 (1);
luego, observa que tienes la ecuación cartesiana explícita de la recta buscada:
y = kx - 1, restas kx en ambos miembros, y queda:
-kx + y = -1, divides por -1 en todos los términos de esta ecuación, y queda:
kx/(-1) + y/(-1) = 1, divides por k al numerador y al denominador del primer término, y queda:
x/(-1/k) + y/(-1) = 1 (2);
luego, observa que los denominadores de los segundos términos de las ecuaciones señaladas (1) (2) son iguales, por lo que, de acuerdo con la condición de paralelismo, planteas la igualdad de los denominadores de los primeros términos, y queda:
-2 = -1/k, multiplicas por k y divides por -2 en ambos miembros, y queda:
k = 1/2,
y observa que si reemplazas este valor remarcado en la ecuación de la recta buscada señalada (2), tienes que las ecuaciones cartesianas continuas de las dos rectas coinciden, por lo que puedes concluir que la recta de referencia y la recta buscada son paralelas coincidentes.
c)
Observa que tienes la ecuación cartesiana implícita de la recta de referencia:
6y - 2x = 0, conmutas términos en el primer miembro de esta ecuación, y queda:
-2x + 6y = 0 (1);
luego, observa que tienes la ecuación cartesiana implícita de la recta buscada:
mx - y + 4 = 0 (2);
luego, recuerda que por condición de perpendicularidad, puedes plantear que la razón entre los coeficientes principales de una de las ecuaciones son iguales al opuesto del valor recíproco de la razón entre coeficientes principales de la otra, por lo que puedes plantear la ecuación:
-2/6 = -(-1)/m, y de aquí despejas:
m = -3.
Espero haberte ayudado.