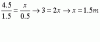-
 Hola, tengo muchos problemas para resolver el ejercicio 9...si alguien me pudiera ayudar seria lo mejor!!! Lo traduzco al castellano:
Hola, tengo muchos problemas para resolver el ejercicio 9...si alguien me pudiera ayudar seria lo mejor!!! Lo traduzco al castellano:9. De una plancha de cartón rectangular de 40x30cm. Se corta un cuadrado de lado x de cada una de sus cuatro esquinas, para construir con el cartón restante una caja en forma de prisma de base rectangular. Cual tiene que ser el valor del lado del cuadrado que se recorta,x, de manera que resulte que la caja resultante tenga el máximo volumen posible?
-

 hola! El ejercicio me pide que realice las derivadas mediante la fórmula de la definición , creo que las tengo mal porque no me cuadra con la derivada ...¿ Alguien me puede ayudar por favor ?
hola! El ejercicio me pide que realice las derivadas mediante la fórmula de la definición , creo que las tengo mal porque no me cuadra con la derivada ...¿ Alguien me puede ayudar por favor ?Antonio Silvio Palmitano
el 18/9/19a)
Aquí comenzaste bien:
f'(a) = Lím(x→a) ( 1 - 3x2 - (1 - 3a2) )/(x - a) = Lím(x→a) ( 1 - 3x2 - 1 - 3a2 )/(x - a) = Lím(x→a) ( -3x2 + 3a2 )/(x - a) =
aquí extraes factor común (-3) en el numerador del argumento, y queda:
= Lím(x→a) ( -3*(x2 - a2 )/(x - a) = factorizas la resta de cuadrados perfectos, y queda:
= Lím(x→a) -3*(x + a)*(x - a)/(x - a) = simplificas, y queda:
= Lím(x→a) -3*(x + a) = evalúas, y queda:
= -3*2*a = resuelves, y queda:
= -6*a.
b)
Aquí comenzaste bien:
f'(a) = Lím(x→a) ( 5x2 - 3*x + 2 - (5a2 - 3*a + 2) )/(x - a) = Lím(x→a) ( 5x2 - 3*x + 2 - 5a2 + 3*a - 2) )/(x - a) =
aquí cancelas términos opuestos, ordenas términos, y queda:
Lím(x→a) ( 5x2 - 5a2 - 3*x + 3*a )/(x - a) =aquí extraes factor común (5) entre los dos primeros términos en el numerador del argumento, extraes factor común (-3) entre los dos últimos términos en el numerador del argumento, y queda:y queda:
= Lím(x→a) ( 5*(x2 - a2) - 3*(x - a) )/(x - a) = factorizas la resta de cuadrados perfectos, y queda:
= Lím(x→a) ( 5*(x + a)*(x - a) - 3*(x - a) )/(x - a) = extraes factor común ( (x - a) ) en el numerador, y queda:
= Lím(x→a) (x - a)*(5*(x + a) - 3)/(x - a) = simplificas, y queda:
= Lím(x→a) (5*(x + a) - 3) = evalúas, y queda:
= 5*2*a + 3 = resuelves, y queda:
= 10*a - 3.
Espero haberte ayudado.
-
Hola unicoos, necesito una ayuda con este problema... muchas gracias
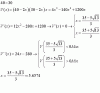
Encuentre el maximo y minimo absoluto de la funcion
Breaking Vlad
el 18/9/19Antonio Silvio Palmitano
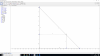
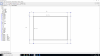
el 18/9/19Observa que el dominio de la función es una región cerrada y acotada, limitada por un tramo de parábola (cuyo vértice en el origen de coordenadas y cuyo eje de simetría es el eje OY), y por un tramo de recta paralela al eje OX.
Observa que tienes la expresión de una función diferenciable en R2, y, por lo tanto, también tienes que la función es continua.
Luego, observa que se cumplen las hipótesis del Teorema de los Extremos Absolutos, por lo que tienes que la función presentará extremos absolutos en el dominio indicado en tu enunciado.
Luego, recuerda que debes considerar, por separado, la existencia de puntos críticos en la región interior del dominio y en su frontera.
1°)
Considera la región interior del dominio.
Observa que tienes la expresión de una función diferenciable en R2, cuyas derivadas parciales primeras tienen las expresiones:
fx(x,y) = y - 1,
fy(x,y) = x - 1;
planteas la condición de punto estacionario (fx(x,y) = 0 e fy(x,y) = 0), y queda el sistema de ecuaciones:
y - 1 = 0,
x - 1 = 0,
aquí observa que las ecuaciones son independientes, y que su solución es el punto (1,1), que no pertenece a la región interior del dominio, por lo que no lo consideramos como punto crítico.
2°)
Observa que la frontera presenta dos vértices (que son las intersecciones de su tramo parabólico con su tramo recto), que son los puntos:
A(-2,4) y B(2,4),
a los que consideramos como puntos críticos.
3°)
Considera el tramo recto de la frontera:
y = 4 (1),
-2 < x < 2;
reemplazas el valor señalado (1) en la expresión de la función, observa que queda reducida a una variable, cuya expresión es:
fA(x) = 1 + x*4 - x - 4, reduces términos semejantes, y queda:
fA(x) = 3*x - 3, que es la expresión de una función derivable, cuya derivada primera tiene la expresión:
fA'(x) = 3,
que no toma el valor cero, por lo que tienes que la función no presenta puntos críticos para este tramo.
4°)
Considera el tramo parabólico de la frontera:
y = x2 (2),
-2 < x < 2;
reemplazas la expresión señalada (2) en la expresión de la función, observa que queda reducida a una variable, cuya expresión es:
fB(x) = 1 + x*x2 - x - x2, resuelves el segundo término, ordenas términos, y queda:
fB(x) = x3 - x2 - x + 1, que es la expresión de una función derivable, cuya derivada primera tiene la expresión:
fB'(x) = 3*x2 - 2*x - 1, planteas la condición de punto estacionario (fB'(x) = 0), y queda:
3*x2 - 2*x - 1 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
x = -1/3, reemplazas este valor en la ecuación señalada (2), resuelves, y queda: y = 1/9,
que conduce al punto C(-1/3,1/9), que sí pertenece al tramo parabólico de la frontera del dominio, por lo que sí lo consideramos como punto crítico;
b)
x = 1, reemplazas este valor en la ecuación señalada (2), resuelves, y queda: y = 1,
que conduce al punto D(1,1), que sí pertenece al tramo parabólico de la frontera del dominio, por lo que sí lo consideramos como punto crítico.
5°)
Evalúas la expresión para los cuatro puntos críticos cuyas expresiones hemos remarcado, y queda:
f(-2,4) = 1 + (-2)*4 - (-2) - 4 = -9,
f(2,4) = 1 + 2*4 - 2 - 4 = 3,
f(-1/3,1/9) = 1 + (-1/3)*(1/9) - (-1/3) - 1/9 = 32/27 ≅ 1,185,
f(1,1) = 1 + 1*1 - 1 - 1 = 0;
luego, puedes concluir que la función presenta:
Máximo Absoluto en el punto A(2,4), en el que toma el valor: f(2,4) = 3,
Mínimo Absoluto en el punto B(-2,4), en el que toma el valor: f(-2,4) = -9.
Espero haberte ayudado.
-
Como podria resolver este limite mediante l'hopital?
lim x->0 (arctg x - x) / (x - sen x)
Antonio Silvio Palmitano
el 17/9/19Vamos con una orientación:
Observa que el numerador y el denominador del argumento de tu límite tienden a cero, por lo que el mismo es indeterminado.
Luego, planteas las expresiones de las derivadas primeras del numerador y del denominador, y queda:
N' = 1/(1 + x2) - 1,
D' = 1 - cosx,
y observa que ambas expresiones tienden a cero cuando x tiende a cero, por lo que tienes que el límite sigue siendo indeterminado luego de aplicar por primera vez la Regla de L'Hôpital.
Luego, planteas las expresiones de las derivadas segundas del numerador y del denominador, y queda:
N'' = -2*x/(1 + x2)2,
D'' = senx,
y observa que ambas expresiones tienden a cero cuando x tiende a cero, por lo que tienes que el límite sigue siendo indeterminado luego de aplicar por segunda vez la Regla de L'Hôpital.
Luego, planteas las expresiones de las derivadas terceras del numerador y del denominador, y queda:
N''' = (-2 + 6*x2)/(1 + x2)3,
D''' = cosx,
y observa que la expresión de la derivada tercera del numerador tiende a -2, y que la expresión de la derivada tercera del denominador tiende a 1, por lo que tienes que el límite es igual a -2, luego de aplicar por tercera vez la Regla de L'Hôpital.
Espero haberte ayudado.