-
ejercicio de matriz inversa
1.- La inversa de A · B es:
a) no se sabe b) A -1 B-1 b) B -1 A-1
2.- La inversa de A.B.C es :
a) no se sabe b)A -1 B -1 C -1 C)C -1 B -1 A -1
3.- La inversa de A+B es :
a) no se sabe b) A-1 + B-1 C) B -1+ A-1
-
Hola por favor no entiendo lo que pide en el apartado B, alguien me puede ayudar., tengo subrayado lo que no entiendo

Antonius Benedictus
el 21/6/19Es el conjunto de polinomios de grado menor o igual que 2 . Pero hay una errata, pues pone x y después los polinomios van con t. Si dejamos t, resulta que la base canónica es (1,t, t^2) por los que la familia V la componen los vectores: (1,0,0), (0,0,2) y (1,1,0) que dan una matriz de rango 3, por lo que son linealmente independientes.
Amin zine
el 21/6/19 -
Cuando se utiliza la factorización LU para resolver un sistema de ecuaciones ?
Da igual si el sistema es compatible determinado, indeterminado o incompatible ?
gracias de antemano.César
el 21/6/19Diremos que una matriz invertible A admite una factorización triangular o factorización LU si puede expresarse como el producto de una matriz triangular inferior L, cuyos elementos diagonales son todos iguales a 1, por una matriz triangular superior.
Si suponemos que la matriz de los coeficientes A de un sistema lineal AX = B admite una factorización triangular; entonces la solución de LUX = B
-
Buen dia!! Tengo una duda, ¿El espacio generado por dos vectores de r2 es r2 ?
César
el 21/6/19Si son linealmente independientes si.
La dimensión de un espacio vectorial se define como el cardinal de una base vectorial para dicho espacio.
La dimensión de un espacio coincide además con los dos cardinales siguientes:
- El máximo número de vectores linealmente independientes de dicho espacio.
- El mínimo número de vectores que forman un conjunto generador para todo el espacio









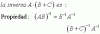





 Ayudenme con esa pregunta. Y pueden decirme donde encuentro material similar
Ayudenme con esa pregunta. Y pueden decirme donde encuentro material similar

















