-
Carmen Escobar Ruiz
el 10/5/19Hola buenas tardes, necesito ayuda para resolver el siguiente ejercicio de manera sencilla, muchas gracias
Tenemos un mapa de España a escala 1:150 000.
a) Si realizamos una fotocopia reducida al 60 %, ¿cuál será la nueva escala?
b) Y si hacemos una ampliación de dicho mapa al 120 %, ¿cuál será la nueva escala?
c) Si la distancia real entre dos pueblos de Cantabria es de 15 km, ¿qué distancia habrá entre los dos pueblos en cada uno de los tres mapas?
César
el 10/5/19si reducimos el papel, habrá que aumentar la escala en la misma proporción
60% reducción escala 150000/0.6=250.000
120% ampliación escala 150000/1.2=125.000
c)
15Km escala 1:150 000 15Km =1.500.000cm distancia 1.500.000/150 000 =10cm
15Km escala 1:250 000 15Km =1.500.000cm distancia 1.500.000/250 000 =6cm
15Km escala 1:250 000 15Km =1.500.000cm distancia 1.500.000/125 000 =12cm
Antonio Silvio Palmitano
el 10/5/19Tienes la escala original del mapa:
1 : 150000, que expresada en forma fraccionaria queda: 1/150000.
a)
Haces la reducción a partir del mapa original, y la escala queda:
1*(60/100) : 150000, divides por 60/100 en ambos miembros de la proporción, y queda:
1 : 250000, que expresada en forma fraccionaria queda: 1/250000.
b)
Haces la ampliación a partir del mapa original, y la escala queda:
1*(120/100) : 150000, divides por 120/100 en ambos miembros, y queda:
1 : 125000, que expresada en forma fraccionaria queda: 1/125000.
c)
1)
En el mapa original (d = 15 Km = 1500000 cm):
x/d = 1/150000, multiplicas por d en ambos miembros, y queda:
x = (1/150000)*d = (1/150000)*1500000 = 10 cm.
2)
En el mapa reducido (d = 15 Km = 1500000 cm):
x/d = 1/250000, multiplicas por d en ambos miembros, y queda:
x = (1/250000)*d = (1/250000)*1500000 = 6 cm.
3)
En el mapa ampliado (d = 15 Km = 1500000 cm):
x/d = 1/125000, multiplicas por d en ambos miembros, y queda:
x = (1/125000)*d = (1/125000)*1500000 = 12 cm.
Espero haberte ayudado.
Carmen Escobar Ruiz
el 12/5/19 -
Carmen Escobar Ruiz
el 10/5/19Porfi que alguien me ayude con éste ejercicio, muchas gracias
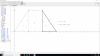
En un triángulo rectángulo la hipotenusa mide 5 cm y uno de los catetos 3 cm.
a) ¿Cuánto mide el otro cateto?
b) Halla la medida de los segmentos en los que queda dividida la hipotenusa al trazar la altura sobre ella.
c) ¿Cuánto mide dicha altura?
d) Realiza un dibujo en el que se representen todas las longitudes calculadas.
-
Carmen Escobar Ruiz
el 10/5/19
Hola buenas tardes, alguien me puede ayudar con éstos 2 ejercicios, muchas gracias
Breaking Vlad
el 26/5/19 -
Carmen Escobar Ruiz
el 10/5/19 -
Carmen Escobar Ruiz
el 10/5/19 -
Chema
el 10/5/19Buenas, tardes, necesito ayuda con este ejercicio. Gracias.
Antonius Benedictus
el 10/5/19¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Mauricio Heredia
el 10/5/19 -
Usuario eliminado
el 10/5/19 -
Sergio Molina
el 10/5/19Hola, estoy perdido con un ejercicio, ¿Me podríasis ayudar?
Sergio Molina
el 10/5/19
Sergio
el 11/5/19Mensaje de pregunta para Antonio Benedictus -
Buenos días, Antonio, tengo una serie de preguntas al ver su resolución de estos ejercicios...
Entiendo perfectamente el procedimiento que ha usado para calcular las ecuaciones de F (primera imagen). Al ser rango 2 en la matriz 2x5 (rango máximo), y por tanto dim(F)=2, son vectores linealmente independientes, y por tanto ha podido multiplicar ya directamente alfa y beta por los vectores para obtener las ecuaciones vectoriales y las ecuaciones paramétricas y tal...
Se puede apreciar dicho procedimiento fácilmente en los vídeos de David Calle, de "ALGEBRA Subespacio vectorial (01,02 y 03) UNIVERSIDAD unicoos matematicas". Hasta ahí todo correcto.
Pero en G, visto que en la matriz 3x5 le ha resultado igualmente el Rango(A)=3 (rango máximo, al igual que en el otro apartado F) y dim(A)=3, y por tanto, todos los 3 vectores son linealmente independientes, por qué decide operar con Gauss en la matriz de G (segunda imagen), y continuar operando con el vector (0,1,-4,0,3) en lugar del original (1,1,-5,0,-2)?
Evidentemente utilizando el 3º vector (0,1,-4,0,3) salen distintas ecuaciones vectoriales, paramétricas, cartesianas... que utilizando el vector (1,1,-5,0,-2).
Además, por otro lado, en otra pregunta,
(entre la 3ª y 4ª imagen) ¿por qué en el cálculo de la base de F+G (3ª imagen) utiliza el 3º vector original de G (1,1,-5,0,-2), mientras que en el cálculo de la base FinterseccionG (4ª imagen) utiliza las ecuaciones que le han dado de resultado operando con el 3º vector modificado de G (0,1,-4,0,3) (obtenido en la 2ª imagen)?
No estoy preguntando por qué en una base utiliza los vectores y en otra las ecuaciones, sino que por qué en una base utiliza lo respectivo a un 3ºvector original de G, y en el cálculo de la otra base, lo respectivo (ecuación) a un 3º vector modificado? No deberíamos trabajar con el mismo 3º vector?
Al dar distintos resultados trabajando entre un vector y otro, creo que lo más correcto es que trabajemos todo el rato con un mismo 3º vector (lo suyo es el original).
Un saludo,
Espero respuesta.
Gracias.
-
Uriel Dominguez
el 10/5/19
