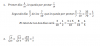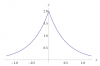
a)  El sen (3pi/2) = -1

El cos (pi) = 1

tan (pi) = 0

Entonces "substituyes" y te queda:

(Raiz de 2 * -1) + 0 + ((raiz de 2)/3) = ((raiz de 2)/3)-(raiz de 2)

b) No lo tengo muy claro, pero debería de dar 2/3 - raíz de algo 

Sí, es un máximo relativo. Los extremos relativos se dan en los puntos críticos: puntos estacionarios (donde y'=0) , puntos angulosos (con derivadas laterales distintas, como es el caso) y puntos de discontinuidad.

Muy amable Antonio, gracias.

Muchs gracias Carlos

Tienes el argumento del límite:

f(x) = 1/(x-1) - x/(x²-1), factorizas el denominador del segundo término, y queda:

f(x) = 1/(x-1) - x / (x+1)(x-1), extraes denominador común, y queda:

f(x) = ( x+1 - x ) / (x+1)(x-1), cancelas términos opuestos en el numerador, y queda:

f(x) = 1 / (x+1)(x-1) (1).

Luego, como tienes que x tiende a 1 desde valores mayores que 1 (o sea "por la derecha"), observa que el primer factor del denominador tiende a 2 y que el segundo factor tiende a 0 desde valores positivos;

luego, tienes que el denominador tiende a 0 desde valores positivos,

y como el numerador es constante, distinto de cero y positivo,

puedes concluir que el el argumento del límite tiende a +infinito:

Lím(x→1+) ( 1/(x-1) - x/(x²-1) ) = sustituyes la expresión señalada (1), y queda:

= Lím(x→1+) ( 1 / (x+1)(x-1) ) = +∞.

Espero haberte ayudado.

1) Porque la función no es derivable en x=0, al no coincidir la derivada por la derecha con la derivada por la izquierda.

2) Ves que la derivada por la izquierda (al sustituir) es -4 y por al derecha es 4. Al tratarse de funciones continuas y derivables no es estrictamente necesario que utilices la definición de la derivada.

Muchas gracias Antonio, ¿podrías decirme además cómo se llama al punto (0,2)? No podría ser un máximo, puesto que la derivada no se anula ni en ese punto ni en ningún otro.

Considerando que la integral indefinida es ln(x^2-1), resulta que en los valores -1 y 1, además de em -infinito sale infinito.

La integral claramente diverge.

Francisco, pon foto del enunciado original que me temo que la ecuación está mal transcrita.