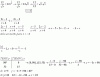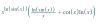-
Hernan Serrato
el 6/3/19
(¬𝑝 → 𝑞) ∧ (𝑟 ∨ 𝑞) A partir de esta proposición compuesta
- Definir las proposiciones simples
- Remplazar las variables expresadas simbólicamente y llevarlas al lenguaje natural.
- Generar una tabla de verdad manualmente a partir del lenguaje simbólico.
- Definir si el argumento seleccionado inicialmente es una tautología, contradicción o contingencia.
Antonius Benedictus
el 6/3/19¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Usuario eliminado
el 6/3/19 -
Charly Argüello
el 5/3/19 -
Tere Arema
el 5/3/19
alguien me puede ayudar a desarrollar este ejercicio?me podrian decir donde puedo ver apuntes para resolverlo?
Gracias
-
Araceli
el 5/3/19 -
Michel Abraham
el 5/3/19Hola, buenas, por favor ayuda con el problema 13, paso a paso y qué teoría se aplica, mi profe de álgebra dejo esto como reto pero no se ni por dónde comenzar. Gracias.
Antonius Benedictus
el 6/3/19¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Quiroga
el 5/3/19Hola, buenas, se que no debería de preguntar esto por aquí, pero me queda poco para los finales y no se donde más consultarlo.
Alguien me podría decir como continuar, es decir, debería de sacar el Dominio para poder integrar todo, pero después de eso que más tendría que hacer?
Antonio Silvio Palmitano
el 7/3/19Vas muy bien.
Observa que los intervalos paramétricos son:
0 ≤ v ≤ π,
0 ≤ u ≤ 2π.
Luego, sustituyes las expresiones paramétricas en el argumento de la integral, multiplicas por el módulo del vector normal a la superficie (│ru x rv│ = R2*senv), extraes factor común y aplicas la identidad trigonométrica pitagórica en el argumento de la raíz cuadrada, y la integral de superficie de tu enunciado queda:
I = 0∫2π0∫π (R*cosv)2*√(R2*sen2v)*R2*senv*dv*du,
distribuyes la potencia en el primer factor, simplificas con las potencias de su argumento en el segundo factor, reduces factores constantes y los extraes, reduces factores semejantes y ordenas factores en el argumento de la integral doble, y queda:
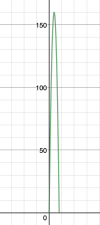
I = R4 * 0∫2π0∫π sen2v*cos2v*dv * du,
y puedes continuar la tarea (observa que deberás aplicar sustituciones trigonométricas para resolver la primera integral).
Haz el intento, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Sara
el 5/3/19 -
Sara
el 5/3/19
