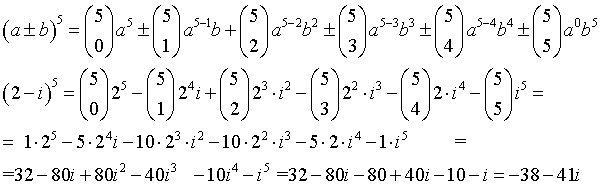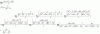-
Carlos Saldaña
el 29/1/19 -
Fernando
el 29/1/19 -
Silvio Aguirre
el 29/1/19hola. Alguien me podría ayudar a resolver este problema:
Un tanque australiano de sección circular de 10 m de radio está en el centro de un campo. Una cabra está atada a un punto del borde del tanque con una cuerda que mide la mitad de la circunferencia del tanque. ¿Podría decir cuál es el área del campo en el que la cabra puede pastar? (Respuesta: 5/6.π³.r² )
Muchas gracias!
Rafael De la Cruz
el 31/1/19El problema de la cabra describe como superficie a pastar, un semicirculo de radio 31, 42 m (longitud de la cuerda a la que está atada, que es la mitad de la longitud de la circunferencia de r 10 m.), y una "semielipse" de r 20 (diámetro del tanque) y r· 31,42 m, calculando ambas áreas, sin olvidar de dividir por dos puesto que son la mitad de cada una...(semicírculo y semielipse) , a la suma de lo anterior habría que restar la superficie que ocupa el tanque de agua de r 10 m y que está restando a la superficie llamemos "operativa" para la cabra. El resultado que me dá a mi es de 2223,64 m2.
-
mrzcas
el 29/1/19Buenas tardes me puedes explicar por favor todo, acerca de la funcion racional:
y=2/x-1
el dominio lo entiendo, pero me pierdo ya en los límites, asíntotas, recorrido, creciente, decreciente, continua, discontinua, puntos de corte....
Tengo mañana examen y no entiendo nada de esta parte. Si hay algún video publicado me dices para ver más ejemplos
-
Fernando
el 29/1/19Buenas tardes. Como se resolvería esta potencia en forma binómica? (2-i) ^ 5. Muchas gracias
-
Araceli
el 29/1/19 -
Fernando
el 29/1/19 -
Alejandro Martín
el 29/1/19 -
Javi
el 29/1/19Alguien me puede ayudar a resolver esta integral usando el método de Hermite? No consigo que me salga la solución de la derecha
-
Ma.Àngels Soler
el 29/1/19Buenos dias David,
Muuucho tiempo llevo aprendiendo con tus magníficos videos y mucho tiempo los aconsego a jóvenes estudiantes. Lo hago porqué hacer matemáticas, parecerá ridículo, pero me encanta. Hoy me he suscrito para poder contactar en momentos necesarios.
Ejercicio que te agradeceria que me hicieras: Calcular area máxima del rectangulo que puede inscribirse entre las rectas x=4, y=0 y la curva √x, con la condición que dos de sus lados se encuentren sobre las rectas mencionadas y un punto suyo sea también un punto de la curva indicada.
