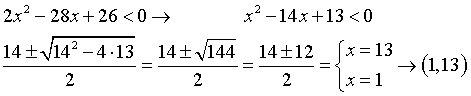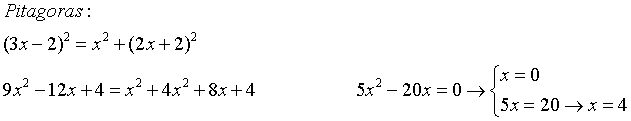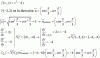-
Miriam Gonzalez
el 30/1/19Hola. Me podríais decir si la siguiente inecuación esta bien hecha?
Javito
el 1/2/19La solución a la inecuación dada es correcta.
El procedimiento obtenerla en general es el siguiente:
1.- Completar el cuadrado del trinomio dado
x al cuadrado -14x +(14/2) al cuadrado - (14/2) al cuadrado + 13 < 0
x al cuadrado - 14x + 7 al cuadrado - 7 al cuadrado + 13 < 0
x al cuadrado - 14x +49 - 49 +13 < 0
(x - 7 ) al cuadrado - 36 < 0
(x - 7 ) al cuadrado < 36
Extraemos raiz cuadrado a ambos lados de la ecuación
raiz cuadrada de ( (x -7) al cuadrado ) < raiz cuadrada de 36
esto es igual a:
Valor absoluto de (x - 7) < 6
luego x -7 < 6 Y x- 7 > -6
x<6+7 Y x > -6 + 7
x< 13 Y x > 1
x en (- infinito , 13 ) intersección (1, infinito) = ( 1, 13)
En el caso de que el signo en la desigualdad sea > (mayor que ) en lugar de la intersección de los intervalos, la solución de la inecuacion sera igual a la union de los intervalos.
-
Miriam Gonzalez
el 30/1/19
Hola. Alguien me puede ayudar con este ejercicio por favor? 
Guillem De La Calle Vicente
el 30/1/19 -
Fernando
el 30/1/19Sabemos que la función F es derivable en todos los puntos, sabiendo que en el tramo (-∞, 0Ι la define la función F(x)= 1+2x+Ax2, y que en el tramo (0,∞) la define F(x)= B+Ax
Encuentra que valores deberán tener A y B para que las anteriores condiciones se cumplan.
-
Diego
el 30/1/19 -
milagroscumbrerass
el 30/1/19 -
milagroscumbrerass
el 30/1/19 -
Leilyta Banegas
el 30/1/19
Hola Unicoos!Me pueden ayudar con el apartado c del ejercicio 26? Intenté dibujarlo de varias formas pero siempre llego a la conclusión que con distintas fronteras en un mismo plano siempre se forman más de 2 semiplanos...
desde ya gracias!
Saludos Leily
Antonio Silvio Palmitano
el 30/1/19
Observa la imagen (disculpa las fallas en los trazos), en la que hemos indicado dos regiones del plano cartesiano OXY:
1)
Semiplano sombreado con rojo,
caracterizado por la inecuación: x ≤ -1,
cuya frontera es la recta cuya ecuación es: y = -1;
2)
Semiplano sombreado con celeste,
caracterizado por la inecuación: x ≥ 3,
cuya frontera es la recta cuya ecuación es: y = 3.
Observa que los dos semiplanos están incluidos en el plano OXY,
observa que son disjuntos (no tienen puntos en común),
y observa que sus fronteras son dos rectas distintas, ambas paralelas al eje OY.
Espero haberte ayudado.
Leilyta Banegas
el 31/1/19Hola Antonio!
Muchas gracias por tu respuesta y explicación!!! No fui al tema de las desigualdades porque no quería salir de los temas dados... en planos y semiplanos...
A propósito del tema estuve investigando y encontré lo q está en la imagen, pregunto puede aplicar como respuesta también? Pues según dice allí las rectas incidentes, que podrían ser fronteras, forman dos semiplanos en un mismo plano.
Desde ya muchas graciasLeily
-
Awiagng
el 30/1/19Buenas, se está deduciendo una identidad que permite obtener la suma de las áreas de rectángulos bajo una parábola para obtener una aproximación al área bajo la misma, no consigo identificar de que manera se pasa de la ecuación 1 a la escuación 2, seguro es algo sencillo que no estoy viendo, este es el libro, pg7: https://calculounicaes.files.wordpress.com/2012/04/calculo-volumen-1-de-tom-apostol.pdf
Neofito 007
el 30/1/19La ecuación (1) que llamas no es sólo esa línea , es toda la sumatoria de esas igualdades , allí mismo lo indica claramente .
Fíjate en la parte derecha de (1)
.... = 2³ - 1³
.... = 3³ - 2³
.... = 4³ - 3³
..... = 5³ - 4³
...
... = (n-2)³ - (n-3)³
.... = (n-1)³ - (n-2)³
.... = n³ - (n-1)³
Justamente lo que indica los términos de la derecha se va eliminando al sumarlos
2³ - 2³ , 3³ - 3³ , ......
-
Aaron Hernandez
el 30/1/19 -
Juan David Rodríguez González
el 30/1/19
