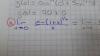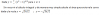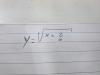-
Teresa Jaque
el 26/1/19 -
Y3
el 26/1/19 -
Y3
el 26/1/19 -
Usuario eliminado
el 26/1/19En el examen de 4º ESO en composición de funciones, hay un problema que no he sabido resolver: Si h(x) =6x; g(t)=t^2-2+h(t). Calcular h o g(4).
La función h(t) no ha sido definida.Por favor ¿pueden decirme si es un error? En caso contrario muestren como resolverlo. Gracias.
-
ana perez
el 25/1/19 -
Bryam Maldonado
el 25/1/19 -
Natalia Vallejos
el 25/1/19Hola, cómo están? Alguien me puede ayudar con la definición de primitiva de una función en un intervalo (a;b] . Gracias!
Antonio Silvio Palmitano
el 25/1/19Vamos con una orientación.
Si la función primitiva tiene expresión: F(x) y la función tiene expresión: f(x), entonces tienes, a partir del Teorema Fundamental del Cálculo Integral:
F ' (x) = f(x);
donde la función f puede ser: continua, o presentar discontinuidades evitables, o presentar discontinuidades inevitables tipo salto, en el intervalo de integración [a,b].
Espero haberte ayudado.
-
Paula LL
el 25/1/19
Hola! me he quedado un poco bloqueada intentando hacer esta EDO, ¿alguien me podría ayudar por favor?
Antonio Silvio Palmitano
el 25/1/19Vamos con una orientación.
Has planteado correctamente la separación de variables, y te ha quedado (observa que resolvemos el coeficiente en el segundo miembro):
dN/(200*N-N2) = 0,0017*dt (1).
Luego, tienes la expresión del denominador del primer miembro:
200*N-N2 = sumas 10000 y restas 10000, y queda:
= 10000 - 10000 + 200*N - N2 = extraes factor común (-1) entre los tres últimos términos, y queda:
= 10000 - (10000 - 200*N + N2) = ordenas términos en el agrupamiento, y queda:
= 10000 - (N2 - 200*N + 1000) = factorizas el trinomio cuadrado perfecto en el agrupamiento, y queda:
= 10000 - (N-100)2 (2).
Luego, sustituyes la expresión señalada (2) en el denominador del primer miembro de la ecuación diferencial señalada (1), y queda:
dN/( 10000-(N-100)2 ) = 0,0017*dt (3).
Luego, puedes integrar el primer miembro de la ecuación diferencial señalada (3) por medio de la sustitución (cambio de variable):
w = N-100,
de donde tienes:
dw = dN;
luego sustituyes expresiones en la ecuación diferencial señalada (3), y queda:
dw/(10000-w2) = 0,0017*dt;
luego, factorizas el denominador del primer miembro, y queda:
dw/( (100-w)*(100+w) ) = 0,0017*dt;
y luego puedes integrar en ambos miembros, y observa que en el primer miembro puedes aplicar el Método de las Fracciones Simples o Parciales (te dejo la tarea).
Espero haberte ayudado.
-
diego
el 25/1/19 -
Diego Schwindt
el 25/1/19Necesito saber el dominio de esta función. Muchas gracias.
Antonio Silvio Palmitano
el 25/1/19Vamos con una precisión.
Observa que si extraes denominador común en el argumento de la raíz cuadrada, entonces la expresión de la función queda:
y = √( (x2 + 2)/x ).
Luego, observa que el numerador del argumento es positivo para todo valor de x (es la suma de un cuadrado más un número positivo);
por lo que tienes que el denominador debe ser también positivo, y además distinto de cero, para que el argumento de la raíz cuadrada sea positivo.
Con todo lo expuesto, tienes que el dominio de la función queda:
D = (0,+∞).
Espero haberte ayudado.
