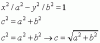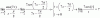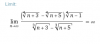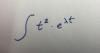-
Hola, me piden que demuestre que la distancia focal de la hiperbola es f=raiz(a^2+b^2) de la ecuacion de la hiperbola x^2/a^2 - y^2/b^2 = 1. He hecho algunos calculos y creo que estoy bastante cerca de demostrarlo pero no logro dar con ello,
tratando de hacer algo similar a la distancia focal de una elipse.
Antonio Silvio Palmitano
el 29/12/18Has considerado el punto P(f,k), perteneciente a la hipérbola, con abscisa focal en el primer cuadrante, por lo que la ordenada de este punto debe ser positiva.
Luego, como el punto P pertenece a la hipérbola, sustituyes sus componentes en la ecuación de dicha curva, y queda:
f2/a2 - k2/b2 = 1, restas f2/a2 en ambos miembros, y queda:
-k2/b2 = -f2/a2 + 1, multiplicas por -1 en todos los términos, y queda:
k2/b2 = f2/a2 - 1, multiplicas por b2 en todos los términos, y queda:
k2 = b2*(f2/a2 - 1) (1), extraes raíz cuadrada positiva, y distribuyes la raíz en el segundo miembro, y queda:
k = b*√(f2/a2 - 1) (2),
que es la expresión de la ordenada del punto P en función de su abscisa y de los semiejes de la hipérbola.
Luego, tienes planteadas las coordenadas de los focos: F1(-f,0) y F2(f,0);
luego, planteas las expresiones de las distancias del punto P a cada uno de ellos, y queda:
d1 = |F1P| = √( (f+f)2 + (k-0)2 ) = √( (2*f)2 + k2 ) = √( 4*f2 + k2 ) (3);
d2 = |F2P| = √( (f-f)2 + (k-0)2 ) = √( (0)2 + k2 ) = √( k2 ) = |k| = k (4) (recuerda que k es positivo).
Luego, planteas la definición de la hipérbola como lugar geométrico, y queda la ecuación:
|d1 - d2| = 2*a, sustituyes las expresiones de las distancias señaladas (3) (4), y queda:
|√( 4*f2 + k2 ) - k| = 2*a, resuelves el valor absoluto (observa que su argumento es positivo), y queda:
√( 4*f2 + k2 ) - k = 2*a, sumas k en ambos miembros, y queda:
√( 4*f2 + k2 ) = 2*a + k, elevas al cuadrado en ambos miembros, y queda:
4*f2 + k2 = ( 2*a + k )2,
desarrollas el segundo miembro (observa que simplificamos raíces y potencias), y queda:
4*f2 + k2 = 4*a2 + 4*a*k + k2, restas k2 en ambos miembros, desarrollas binomios, y queda:
4*f2 = 4*a2 + 4*a*k, divides por 4 en todos los términos, y queda:
f2 = a2 + a*k, sustituyes la expresión señalada (2), y queda:
f2 = a2 + a*b*√(f2/a2 - 1), restas a2 en ambos miembros, y queda:
f2 - a2 = a*b*√(f2/a2 - 1),
elevas al cuadrado en ambos miembros (observa que operamos en el segundo miembro), y queda:
(f2 - a2)2 = a2*b2*(f2/a2 - 1),
desarrollas el primer miembro, distribuyes el segundo miembro, y queda:
f4 - 2*a2*f2 + a4 = b2*f2 - a2*b2,
restas b2*f2 y sumas a2*b2 en ambos miembros, y queda:
f4 - 2*a2*f2 - b2*f2 + a4 + a2*b2 = 0,
expresas al primer término como un cuadrado, extraes factor común entre el segundo y el tercer término, extraes factor común entre los dos últimos términos, y queda:
(f2)2 - (2*a2+b2)*f2 + a2*(a2+b2) = 0,
que es una ecuación "bicuadrática" para la incógnita f, cuyos coeficientes son:
A = 1,
B = -(2*a2+b2),
C = a2*(a2+b2);
y cuyo discriminante queda expresado:
D = B2 - 4*A*C, sustituyes expresiones, y queda:
D = (2*a2+b2)2 - 4*a2*(a2+b2), desarrollas los dos términos, y queda:
D = 4*a4 + 4*a2*b2 + b4 - 4*a4 - 4*a2*b2, cancelas términos opuestos, reduces términos semejantes, y queda:
D =b4, extraes raíz cuadrada en ambos miembros, y queda:
√(D) = b2;
luego, planteas la ecuación de las soluciones de la ecuación "bicuadrática", y queda:
f2 = ( -B ± √(D) ) / (2*A), sustituyes expresiones, resuelves el denominador, y queda:
f2 = ( 2*a2+b2 ± b2 ) / 2,
y a partir de aquí tienes dos opciones
1°)
f2 = ( 2*a2+b2 - b2 ) / 2, cancelas términos opuestos en el numerador, y queda:
f2 = 2*a2/2, simplificas, y queda:
f2 = a2, extraes raíz cuadrada positiva (recuerda que el punto P pertenece al primer cuadrante), y queda:
f = a,
que no tiene sentido para este problema, porque la abscisa focal coincide con la abscisa de uno de los vértices reales de la hipérbola;
2°)
f2 = ( 2*a2+b2 + b2 ) / 2, reduces términos semejantes en el numerador, y queda:
f2 =( 2*a2 + 2*b2 )/2, distribuyes el denominador, simplificas en ambos términos, y queda:
f2 = a2 + b2, extraes raíz cuadrada positiva (recuerda que el punto P pertenece al primer cuadrante), y queda:
f = √(a2 + b2),
que es la expresión de la abscisa del punto P, y el valor de la distancia focal, en función de los valores correspondientes al semieje real (a) y al semieje imaginario (b) de la hipérbola cuya ecuación y gráfico has planteado.
Espero haberte ayudado.
-
Buenas tengo este limite y no pude resolverlo solo llegue hasta esa parte, incluso inverti la fraccion y aplique el teorema de limite exponencial y llegue al resultado de e1 y en el libro el resultado es de 7 .... alguien me puede ayudar por favor... por cualquier metodo que no sea L Hopital puede ser cambio de variable, simplificacion o cualquier otro metodo gracias de antemano a los que me ayuden...
Omar Diaz Salazar
el 29/12/18Antonio Silvio Palmitano
el 29/12/18Tienes un límite indeterminado, ya que tanto el numerado como el denominador tienden a cero.
Has planteado bien la sustitución (cambio de variable), y el límite te ha quedado:
L = Lím(p→0) cos(7*p + 7π/2) / p;
luego, aplicas la identidad del coseno de la suma de dos ángulos en el numerador, y queda:
L = Lím(p→0) ( cos(7*p)*cos(7π/2) - sen(7*p)*sen(7π/2) ) / p (1).
Luego, tienes los factores numéricos:
cos(7π/2) = cos(7π/2 - 2π) = cos(3π/2) = 0,
sen(7π/2) = sen(7π/2 - 2π) = sen(3π/2) = -1;
luego, reemplazas estos valores en la expresión del límite señalada (1), y queda:
L = Lím(p→0) ( cos(7*p)*0 - sen(7*p)*(-1) ) / p,
cancelas el término nulo y resuelves en el numerador, y queda:
L = Lím(p→0) sen(7*p) / p;
luego, multiplicas por 7 en el numerador y en el denominador del argumento del límite, y queda:
L = Lím(p→0) 7*sen(7*p) / (7*p),
extraes el factor numérico en el numerador, y queda:
L = 7 * Lím(p→0) sen(7*p) / (7*p) (2).
Luego, planteas la sustitución (cambio de variable):
w = 7*p (observa que w tiende a cero cuando p tiende a cero);
luego sustituyes en la expresión del límite señalada (2), y queda:
L = 7 * Lím(w→0) sen(w) / (w),
y tienes que el segundo factor tiende a 1 (observa que tienes un límite trascendente que seguramente has visto en clase), por lo que reemplazas, y queda:
L = 7 * 1 = 7.
Espero haberte ayudado.
-
Buenas Tardes
Estoy realizando ejercicios de anualidades vencidas, pero tengo problemas con estos 2 Ejercicios que no me salen las mismas respuestas del libro. Me podria auydar gracias.-
a) Una compañía debe redimir una emisión de obligaciones por $ 30.000.000 dentro de 10 años, y para ello, establece reservas anuales que se depositarán en un fondo que abona el 7%: hallar el valor de la reserva anual.
b) Enrique compró una casa cuyo valor es de $ 18.000.000 al contado. Pagó $ 5.000.000 de contado y el saldo en 8 pagos iguales por trimestre vencido. Si en la operación se le carga el 10% de interés nominal, hallar el valor de los pagos trimestrales.
-
Hola buenas alguien podría ayudarme , gracias
aUna persona adquiere un préstamo de $ 450.000 a 6 meses con un 3% de interés simple anual. En caso de mora, se cobrará un 15% de interés por el tiempo que exceda al plazo.
b)¿Qué cantidad paga el deudor si este se atrasa en 60 días?
Antonio
el 28/12/18Hola, entiendo que se cobra un 15% anual también por el tiempo que se excede.
Suponiendo que es así, para empezar, se debería calcular los intereses que pagaría al devolverlo justo cumplidos los 6 meses. Sería 450.000$ · 0,03 / 2= 6.750$. Se divide entre dos al ser seis meses la mitad de un año.
Después se puede calcular la cantidad extra que pagaría el deudor por retrasarse 60 días. 450.000$ · 0,15 · 60 / 365 = 11.095,89$. Se multiplica el interés 0,15 por el número de días que pasan y se divide por el número de días que tiene un año.
Finalmente, se suman las dos cantidades y se averigua el interés que tiene que pagar el deudor: 6.750$ + 11.095,89$ = 17.845,89$. Se puede sumar la cantidad prestada para saber la cantidad total que tiene que devolver: 450.000$+17.845,89$= 467.845,89$
Espero que te sirva, un saludo.
-
Hola buenas alguien podría ayudarme , gracias
a) Un capital de $ 8.000.000 se coloca por mitades en dos instituciones de crédito durante 6 meses En la primera institución gana el 20% anual y en la segunda el 2,5% mensual Calcular el interés total al final del plazo estipulado
Antonio
el 28/12/18Hola.
Primero de todo, hay que dividir entre dos el capital: 8.000.000$ / 2 = 4.000.000$.
En la primera institución, el interés generado será: 4.000.000$ · 0,2 · 1/2 = 400.000$ (la fracción 1/2 es porque se divide un año entre 2, que es seis meses aproximadamente).
En la segunda institución, el interés generado (suponiendo que el interés mensual es simple) será: 4.000.000$ · 0,025 · 6 = 600.000$ (se multiplica por 6 ya que el interés es mensual, y son 6 meses).
Por tanto, se suman los intereses obtenidos en cada una de las instituciones y el resultado será: 400.000$ + 600.000$ = 1.000.000$ de interés total.
Espero que te sirva la respuesta. Un saludo.
-
-
Antonio Silvio Palmitano
el 28/12/18Vamos con una orientación.
Observa que puedes plantear la expresión de la función "distancia cuadrática" entre un punto P(x,y,z) perteneciente al plano y al paraboloide cuyas ecuaciones tienes en tu enunciado, y el origen de coordenadas, y queda:
f(x,y,z) = x2 + y2 + z2,
que es la expresión de una función diferenciable en R3, cuyo gradiente tiene la expresión:
∇f = < 2x , 2y , 2z > (1).
Luego, observa que el plano cuya ecuación tienes en tu enunciado (que puedes escribir en la forma: x + y + 2z - 2 = 0) es una superficie de nivel de la función cuya expresión es:
g(x,y,z) = x + y + 2z - 2,
que es la expresión de una función diferenciable en R3, cuyo gradiente tiene la expresión:
∇g = < 1 , 1 , 2 > (2).
Luego, observa que el paraboloide cuya ecuación tienes en tu enunciado (que puedes escribir en la forma: x2 + y2 - z = 0) es una superficie de nivel de la función cuya expresión es:
h(x,y,z) = x2 + y2 - z,
que es la expresión de una función diferenciable en R3, cuyo gradiente tiene la expresión:
∇h = < 2x , 2y , -1 > (3).
Luego, planteas el Sistema de Ecuaciones de Lagrange (observa que indicamos con a y con b a los multiplicadores), y queda:
∇f = a*∇h + b*∇h,
g(x,y,z) = 0,
g(x,y,z) = 0;
sustituyes las expresiones de los vectores gradientes y de las funciones, y queda:
< 2x , 2y , 2z > = a*< 1 , 1 , 2 > + b*< 2x , 2y , -1 >,
x + y + 2z - 2 = 0,
x2 + y2 - z = 0,
resuelves las operaciones en el segundo miembro de la ecuación vectorial, igualas componente a componente, sumas 2 en ambos miembros de la segunda ecuación, sumas z en ambos miembros de la tercera ecuación, y queda el sistema de cinco ecuaciones con cinco incógnitas:
2x = a + 2b*x,
2y = a + 2b*y,
2z = 2a - b,
x + 2y + 2z = 2
x2 + y2 = z,
con a ∈ R y b ∈ R.
Luego, queda que resuelvas el sistema de ecuaciones, lo que no es una tarea menor ni sencilla, y para ello puedes comenzar por despejar b en la tercera ecuación y sustituir en las dos primeras, luego despejar a en la primera y sustituirlo en la segunda, y tendrás una ecuación con tres incógnitas, que deberás resolverla junto a las dos últimas.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Buenas tardes, a ver si podeis ayudarme a resolver este límite de sucesión de la forma que explica el enunciado, según el profesor, el resultado no es infinito, si no un numero exacto. Muchisimas graias.
Antonio Silvio Palmitano
el 28/12/18Tienes las expresiones de los infinitésimos cuasi equivalentes:
(1 + xn)p - 1 ≅ p*xn, aquí sumas 1 en ambos miembros, y queda:
(1 + xn)p ≅ 1 + p*xn (*).
Vamos con cada raíz por separado:
1)
4√(n+3) = 4√( n*(1 + 3/n) ) = 4√(n)*4√(1 + 3/n) = n1/4*(1 + 3/n)1/4,
observa que en este caso tienes: p = 1/4, xn = 3/n, aplicas la cuasi identidad señalada (*), y queda:
4√(n+3) ≅ n1/4*( 1 + (1/4)*(3/n) ) ≅ n1/4*( 1 + 3/(4*n) ) (1).
2)
4√(n+5) = 4√( n*(1 + 5/n) ) = 4√(n)*4√(1 + 5/n) = n1/4*(1 + 5/n)1/4,
observa que en este caso tienes: p = 1/4, xn = 5/n, aplicas la cuasi identidad señalada (*), y queda:
4√(n+5) ≅ n1/4*( 1 + (1/4)*(5/n) ) ≅ n1/4*( 1 + 5/(4*n) ) (2).
3)
4√(n-1) = 4√( n*(1 + (-1)/n) ) = 4√(n)*4√(1 + (-1)/n) = n1/4*(1 + (-1)/n)1/4,
observa que en este caso tienes: p = 1/4, xn = -1/n, aplicas la cuasi identidad señalada (*), y queda:
4√(n+5) ≅ n1/4*( 1 + (1/4)*(-1/n) ) ≅ n1/4*( 1 -1/(4*n) ) (3).
4)
3√(n+3) = 3√( n*(1 + 3/n) ) = 3√(n)*3√(1 + 3/n) = n1/3*(1 + 3/n)1/3,
observa que en este caso tienes: p = 1/3, xn = 3/n, aplicas la cuasi identidad señalada (*), y queda:
3√(n+3) ≅ n1/3*( 1 + (1/3)*(3/n) ) ≅ n1/3*( 1 + 1/n ) (4).
5)
3√(n+5) = 3√( n*(1 + 5/n) ) = 3√(n)*3√(1 + 5/n) = n1/3*(1 + 5/n)1/3,
observa que en este caso tienes: p = 1/3, xn = 5/n, aplicas la cuasi identidad señalada (*), y queda:
3√(n+5) ≅ n1/3*( 1 + (1/3)*(5/n) ) ≅ n1/3*( 1 + 5/(3*n) ) (5).
Luego, planteas la expresión del numerador del factor fraccionario de tu enunciado, y queda:
N(n) = 4√(n+3) - 4√(n+5), sustituyes las expresiones señaladas (1) (2), y queda:
N(n) = n1/4*( 1 + 3/(4*n) ) - n1/4*( 1 + 5/(4*n) ), extraes factor común, y queda:
N(n) = n1/4*( 1 + 3/(4*n) - ( 1 + 5/(4*n) ), resuelves signos y cancelas términos opuestos en el agrupamiento, y queda:
N(n) = n1/4*( 3/(4*n) - 5/(4*n) ), resuelves el agrupamiento, y queda:
N(n) = n1/4*( -1/(2n) ), simplificas, ordenas factores, y queda:
N(n) = (-1/2)*(1/n3/4) (6).
Luego, planteas la expresión del denominador del factor fraccionario de tu enunciado, y queda:
D(n) = 3√(n+3) - 3√(n+5), sustituyes las expresiones señaladas (4) (5), y queda:
N(n) = n1/3*( 1 + 1/n ) - n1/3*( 1 + (1/3)*(5/n) ), extraes factor común, y queda:
N(n) = n1/3*( 1 + 1/n - ( 1 + (1/3)*(5/n) ), resuelves signos y cancelas términos opuestos en el agrupamiento, y queda:
N(n) = n1/3*( 1/n - (1/3)*(5/n) ), resuelves el agrupamiento, y queda:
N(n) = n1/3*( -2/(3n) ), simplificas, ordenas factores, y queda:
N(n) = (-2/3)*(1/n2/3) (7).
Luego, sustituyes las expresiones señaladas (6) (3) (7), y el límite de tu enunciado queda:
L = Lím(n→∞) (-1/2)*(1/n3/4) * n1/4*( 1 -1/(4*n) ) / (-2/3)*(1/n2/3),
resuelves factores y simplificas entre el primer factor del numerador y el denominador, y queda:
L = Lím(n→∞) (3/4)*(1/n1/12) * n1/4*( 1 -1/(4*n) ),
extraes el factor constante, resuelves el producto de potencias con bases iguales, y queda:
L = (3/4) * Lím(n→∞) n1/3*( 1 -1/(4*n) ),
distribuyes, simplificas en el segundo término, y queda:
L = (3/4) * Lím(n→∞) ( n1/3 - 1/(4*n2/3) ),
resuelves el límite (observa que el primer factor tiende a infinito y que el segundo factor tiende a cero, y queda:
L = ∞.
Espero haberte ayudado.