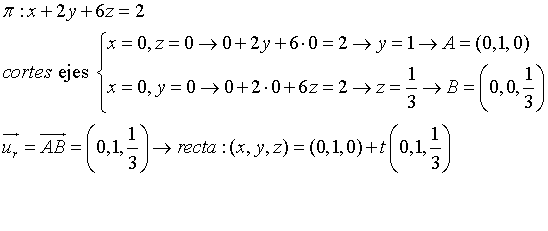Datos identificativos del titular del sitio web
En cumplimiento del deber de información estipulado en el artículo 10 de la Ley 34/2002 de 11 de julio de Servicios de la Sociedad de la Información y de Comercio Electrónico, UNICOOS EDUCATION, S.L. (en lo sucesivo “UNICOOS”) y en calidad de titular del web site www.unicoos.com, procede a comunicarles los datos identificativos exigidos por la referida norma:
Denominación social: UNICOOS EDUCATION S.L.
Domicilio: C/ Marqués de Cubas, 18 28891 VELILLA DE SAN ANTONIO (MADRID)
CIF: B87168126
Dirección de correo electrónico: unicoos@unicoos.com
La presente información conforma y regula las condiciones de uso, las limitaciones de responsabilidad y las obligaciones que, los usuarios de la página Web que se publica bajo el nombre de dominio www.unicoos.com, asumen y se comprometen a respetar.
Definiciones
“Página”, dominio www.unicoos.com que se pone a disposición de los Usuarios de Internet.
“Usuario”, persona física o jurídica que utiliza o navega por la Página.
“Contenido”, son las páginas que conforman la totalidad del dominio www.unicoos.com, las cuales conforman la información y los servicios que UNICOOS pone a disposición de los Usuarios de Internet. En ellas se contienen los mensajes, textos, fotografías, gráficos, iconos, logos, tecnología, links, texturas, dibujos, archivos de sonido y/o imagen, grabaciones, software, aspecto, diseño gráfico y códigos fuente y, en general, cualquier clase de material contenido en la Página.
“Web”, palabra técnica que describe el sistema de acceso a la información vía Internet, que se configura por medio de páginas confeccionadas con lenguaje HTML o similar, y mecanismos de programación tales como java, javascript, PHP, u otros, etc... En estas páginas diseñadas y publicadas bajo un nombre de dominio Internet son el resultado de la información que el titular pone a disposición de los Usuarios de Internet.
“Hiperenlace”, técnica por la cual un Usuario puede navegar por diferentes páginas de la Web, o por Internet, con un simple click sobre el texto, icono, botón o indicativo que contiene el enlace.
Descripción de unicoos
UNICOOS es un portal web desde el que se ofrecen contenidos y servicios educativos GRATUITOS y también de pago orientados a usuarios desde 1º de ESO hasta 2º de Bachillerato y Selectividad así como a sus padres o tutores. Se trata de una plataforma online pensada para reforzar y complementar en el hogar el aprendizaje que reciben los alumnos dentro del ámbito académico, en sus respectivos centros escolares.
Este apoyo al estudio se proporciona a través de tres principales secciones: Vídeos, Material adicional, Exámenes y Foros.
Los Vídeos y Foros son de acceso 100% gratuito, sin ningún tipo de limitación, pero los exámenes de autoevaluación, chat, material adicional (teoría y ejercicios resueltos seleccionados para los usuarios) y otras funcionalidades existentes o de nueva implantación precisan de una suscripción no gratuita que denominamos UNICOOS PRO, y que dan acceso total a todos los contenidos y aplicaciones, así como la eliminación de publicidad en toda la navegación.
Actualmente, UNICOOS contempla diferentes opciones de contratación de sus servicios en periodos mensuales, trimestrales, semestrales y anuales. Estas suscripciones pueden renovarse automáticamente a no ser que el usuario la cancele, o bien a través de la contratación de un paquete de acceso al servicio con fecha de caducidad.
Aunque los contenidos y los servicios de pago están orientados a niños con edades comprendidas entre los 12 y los 18 años, el acceso a toda esta oferta comercial y su compra o contratación deberá ser tramitada por mayores de edad, es decir, los padres, tutores o representantes legales de los usuarios menores de edad.
Los usuarios que realicen el proceso de compra sin finalizar la contratación de cualquiera de los productos sujetos a pago, pueden pasar a formar parte de UNICOOS accediendo de forma gratuita a la Comunidad y recibir información y comunicaciones comerciales, así como ventajas para la contratación de los productos que pudieran adquirir en el futuro.
Suscripción PRO
Al convertirte en usuario PRO de UNICOOS, ésta continuará hasta su conclusión.
Para utilizar el servicio UNICOOS, debes tener acceso a Internet y un dispositivo con un navegador web compatible.
A menos que canceles tu suscripción con anterioridad a la fecha de renovación, nos autorizas a cargar la cuota de suscripción correspondiente al siguiente ciclo de renovación en tu Perfil de usuario (consulta "Cancelación" más adelante).
Ciclo de facturación
La cuota de suscripción al servicio UNICOOS se cobrará en tu Método de pago en la fecha de renovación indicada en tu Perfil de usuario.
La longitud de tu ciclo de facturación dependerá del tipo de suscripción que elijas al registrarte en el servicio.
En algunos casos, la fecha de facturación puede cambiar, como por ejemplo si tu Método de pago no se ha configurado correctamente o si tu suscripción de pago se inició en un día no existente en un mes determinado. Visita nuestro sitio web y haz clic en el enlace "Perfil" en la página "Perfil" para consultar la fecha de tu próximo pago y el estado de tu suscripción.
Cancelación
Puedes cancelar tu suscripción a UNICOOS en cualquier momento y seguirás teniendo acceso al servicio hasta el final de tu periodo de facturación.
Los pagos no son reembolsables y no facilitamos devoluciones ni abonos por periodos parciales de suscripción mensual.
Para cancelar tu suscripción, ve a la página "Perfil" y sigue las instrucciones para la cancelación.
Si cancelas tu suscripción, tu cuenta se convertirá automáticamente en gratuita al final de tu periodo de facturación.
Política de Cookies
UNICOOS utiliza cookies, que son un pequeño archivo de texto que el servidor puede guardar en el disco duro de un equipo para almacenar algún tipo de información sobre el usuario. Las cookies sólo pueden ser leídas por el sitio web que las envió al equipo, y por el propio usuario. No son un archivo ejecutable ni pueden propagar ni contener un virus.
Las cookies de Tareas y más sólo almacenan datos de índole técnica que permitan al sistema reconocer al usuario en sus diferentes visitas al sitio web, con el fin último de mejorar nuestros servicios. Si no estás conforme, puedes configurar tu navegador para aceptar o rechazar las cookies, aunque UNICOOS no se responsabiliza de que la desactivación de las cookies impida o dificulte el buen funcionamiento de la página.
Según quien sea la entidad que gestione el dominio desde donde se envían las cookies y trate los datos que se obtengan se pueden distinguir dos tipos: cookies propias y cookies de terceros .
Existe también una segunda clasificación según el plazo de tiempo que permanecen almacenadas en el navegador del cliente, pudiendo tratarse de cookies de sesión o cookies persistentes.
Por último, existe otra clasificación con cinco tipos de cookies según la finalidad para la que se traten los datos obtenidos: cookies técnicas, cookies de personalización, cookies de análisis, cookies publicitarias y cookies de publicidad comportamental.
Para más información a este respecto puede consultar la Guía sobre el uso de las cookies de la Agencia Española de Protección de Datos.
La página web de UNICOOS utiliza Google Analytics, un servicio de analítica web desarrollada por Google, que permite la medición y análisis de la navegación en las páginas web. En su navegador podrá observar 4 cookies de este servicio. Según la tipología anterior se trata de cookies propias, de sesión y de análisis. A través de la analítica web se obtiene información relativa al número de usuarios que acceden a la web, el número de páginas vistas, la frecuencia y repetición de las visitas, su duración, el navegador utilizado, el operador que presta el servicio, el idioma, el terminal que utiliza, o la ciudad a la que está asignada su dirección IP. Información que posibilita un mejor y más apropiado servicio por parte de este portal. Puede encontrar más información al respecto e inhabilitar el uso de estas cookies http://www.google.es/intl/es/analytics/privacyoverview.html
- Aceptación de la Política de cookies
UNICOOS asume que usted acepta el uso de cookies. No obstante, muestra información sobre su Política de cookies en la parte superior de cualquier página del portal con cada inicio de sesión con el objeto de que usted sea consciente. Ante esta información es posible llevar a cabo las siguientes acciones:
- Aceptar cookies. No se volverá a visualizar este aviso al acceder a cualquier página del portal.
-Consultar la Política de cookies. Podrá obtener más información sobre qué son las cookies, conocer la Política de cookies de UNICOOS y modificar la configuración de su navegador.
- Cómo modificar la configuración de las cookies
Usted puede restringir, bloquear o borrar las cookies de UNICOOS o cualquier otra página web, utilizando su navegador. En cada navegador la operativa es diferente, la función de 'Ayuda" le mostrará cómo hacerlo.
Condiciones de Uso
La simple y mera utilización de la Página otorga la condición de usuario de la Página, bien sea persona física o jurídica, y obligatoriamente implica la aceptación completa, plena y sin reservas de todas y cada una de las cláusulas y condiciones generales incluidas en el Aviso Legal. Si el Usuario no estuviera conforme con las cláusulas y condiciones de uso de este Aviso Legal, se abstendrá de utilizar la Página.
Este Aviso Legal está sujeto a cambios y actualizaciones por lo que la versión publicada por UNICOOS puede ser diferente en cada momento en que el Usuario acceda al Portal. Por tanto, el Usuario debe leer el Aviso Legal en todas y cada una de las ocasiones en que acceda a la Página.
A través de la Página, UNICOOS facilita a los Usuarios el acceso y la utilización de diversos Contenidos publicados por medio de Internet por UNICOOS o por terceros autorizados.
El Usuario esta obligado y se compromete a utilizar la Página y los Contenidos de conformidad con la legislación vigente, el Aviso Legal, y cualquier otro aviso o instrucciones puestos en su conocimiento, bien sea por medio de este aviso legal o en cualquier otro lugar dentro de los Contenidos que conforman la Página, así como con las normas de convivencia, la moral y buenas costumbres generalmente aceptadas.
A tal efecto, el Usuario se obliga y compromete a NO utilizar cualquiera de los Contenidos con fines o efectos ilícitos, prohibidos en el Aviso Legal o por la legislación vigente, lesivos de los derechos e intereses de terceros, o que de cualquier forma puedan dañar, inutilizar, sobrecargar, deteriorar o impedir la normal utilización de los Contenidos, los equipos informáticos o los documentos, archivos y toda clase de contenidos almacenados en cualquier equipo informático propios o contratados por UNICOOS, de otros Usuarios o de cualquier usuario de Internet (hardware y software).
El Usuario se obliga y se compromete a no transmitir, difundir o poner a disposición de terceros cualquier clase de material contenido en la Página, tales como informaciones, textos, datos, contenidos, mensajes, gráficos, dibujos, archivos de sonido y/o imagen, fotografías, grabaciones, software, logotipos, marcas, iconos, tecnología, fotografías, software, enlaces, diseño gráfico y códigos fuente, o cualquier otro material al que tuviera acceso en su condición de Usuario de la Página, sin que esta enumeración tenga carácter limitativo.
Asimismo, de conformidad con todo ello, el Usuario no podrá:
- Reproducir, copiar, distribuir, poner a disposición o de cualquier otra forma comunicar públicamente, transformar o modificar los Contenidos, a menos que se cuente con la autorización escrita y explícita de UNICOOS, que es titular de los correspondientes derechos, o bien que ello resulte legalmente permitido.
- Suprimir, manipular o de cualquier forma alterar el "copyright" y demás datos identificativos de la reserva de derechos de UNICOOS o de sus titulares, de las huellas y/o identificadores digitales, o de cualesquiera otros medios técnicos establecidos para su reconocimiento.
- El Usuario deberá abstenerse de obtener e incluso de intentar obtener los Contenidos empleando para ello medios o procedimientos distintos de los que, según los casos, se hayan puesto a su disposición a este efecto o se hayan indicado a este efecto en las páginas Web donde se encuentren los Contenidos o, en general, de los que se empleen habitualmente en Internet a este efecto siempre que no entrañen un riesgo de daño o inutilización de la Página, y/o de los Contenidos.
Propiedad Intelectual
Todas las marcas, nombres comerciales o signos distintivos de cualquier clase que aparecen en la Página son propiedad de UNICOOS o, en su caso, de terceros que han autorizado su uso, sin que pueda entenderse que el uso o acceso al Portal y/o a los Contenidos atribuya al Usuario derecho alguno sobre las citadas marcas, nombres comerciales y/o signos distintivos, y sin que puedan entenderse cedidos al Usuario, ninguno de los derechos de explotación que existen o puedan existir sobre dichos Contenidos.
De igual modo los Contenidos son propiedad intelectual de UNICOOS, o de terceros en su caso, por tanto, los derechos de Propiedad Intelectual son titularidad de UNICOOS o de terceros que han autorizado su uso, a quienes corresponde el ejercicio exclusivo de los derechos de explotación de los mismos en cualquier forma y, en especial, los derechos de reproducción, distribución, comunicación pública y transformación.
La utilización no autorizada de la información contenida en esta Web, así como la lesión de los derechos de Propiedad Intelectual o Industrial de UNICOOS o de terceros incluidos en la Página que hayan cedido contenidos dará lugar a las responsabilidades legalmente establecidas.
Hiperenlaces
Aquellas personas que se propongan establecer hiperenlaces entre su página Web y la Página deberán observar y cumplir las condiciones siguientes:
- No será necesaria autorización previa cuando el Hiperenlace permita únicamente el acceso a la página de inicio, pero no podrá reproducirla de ninguna forma. Cualquier otra forma de Hiperenlace requerirá la autorización expresa e inequívoca por escrito por parte de UNICOOS.
- No se crearán “marcos” (“frames”) con las páginas Web ni sobre las páginas Web de UNICOOS.
- No se realizarán manifestaciones o indicaciones falsas, inexactas, u ofensivas sobre UNICOOS sus directivos, sus empleados o colaboradores, o de las personas que se relacionen en la Página por cualquier motivo, o de los Usuarios de las Página, o de los Contenidos suministrados.
- No se declarará ni se dará a entender que UNICOOS ha autorizado el Hiperenlace o que ha supervisado o asumido de cualquier forma los Contenidos ofrecidos o puestos a disposición de la página Web en la que se establece el Hiperenlace.
- La página Web en la que se establezca el Hiperenlace solo podrá contener lo estrictamente necesario para identificar el destino del Hiperenlace.
- La página Web en la que se establezca el Hiperenlace no contendrá informaciones o contenidos ilícitos, contrarios a la moral y a las buenas costumbres generalmente aceptadas y al orden público, así como tampoco contendrá contenidos contrarios a cualesquiera derechos de terceros.
Disponibilidad de la Página
UNICOOS no garantiza la inexistencia de interrupciones o errores en el acceso a la Página, a sus Contenidos, ni que éste se encuentren actualizados, aunque desarrollará sus mejores esfuerzos para, en su caso, evitarlos, subsanarlos o actualizarlos. Por consiguiente, UNICOOS no se responsabiliza de los daños o perjuicios de cualquier tipo producidos en el Usuario que traigan causa de fallos o desconexiones en las redes de telecomunicaciones que produzcan la suspensión, cancelación o interrupción del servicio del Portal durante la prestación del mismo o con carácter previo.
UNICOOS excluye, con las excepciones contempladas en la legislación vigente, cualquier responsabilidad por los daños y perjuicios de toda naturaleza que puedan deberse a la falta de disponibilidad, continuidad o calidad del funcionamiento de la Página y de los Contenidos, al no cumplimiento de la expectativa de utilidad que los usuarios hubieren podido atribuir a la Página y a los Contenidos.
La función de los Hiperenlaces que aparecen en esta Web es exclusivamente la de informar al usuario acerca de la existencia de otras Web que contienen información sobre la materia. Dichos Hiperenlaces no constituyen sugerencia ni recomendación alguna.
UNICOOS no se hace responsable de los contenidos de dichas páginas enlazadas, del funcionamiento o utilidad de los Hiperenlaces ni del resultado de dichos enlaces, ni garantiza la ausencia de virus u otros elementos en los mismos que puedan producir alteraciones en el sistema informático (hardware y software), los documentos o los ficheros del usuario, excluyendo cualquier responsabilidad por los daños de cualquier clase causados al usuario por este motivo.
El acceso a la Página no implica la obligación por parte de UNICOOS de controlar la ausencia de virus, gusanos o cualquier otro elemento informático dañino. Corresponde al Usuario, en todo caso, la disponibilidad de herramientas adecuadas para la detección y desinfección de programas informáticos dañinos, por lo tanto, UNICOOS no se hace responsable de los posibles errores de seguridad que se puedan producir durante la prestación del servicio de la Página, ni de los posibles daños que puedan causarse al sistema informático del usuario o de terceros (hardware y software), los ficheros o documentos almacenados en el mismo, como consecuencia de la presencia de virus en el ordenador del usuario utilizado para la conexión a los servicios y contenidos de la Web, de un mal funcionamiento del navegador o del uso de versiones no actualizadas del mismo.
Calidad de la Página
Dado el entorno dinámico y cambiante de la información y servicios que se suministran por medio de la Página, UNICOOS realiza su mejor esfuerzo, pero no garantiza la completa veracidad, exactitud, fiabilidad, utilidad y/o actualidad de los Contenidos.
La información contenida en las páginas que componen este Portal sólo tiene carácter informativo, consultivo, divulgativo y publicitario. En ningún caso ofrecen ni tienen carácter de compromiso vinculante o contractual.
Limitación de la responsabilidad
UNICOOS excluye toda responsabilidad por las decisiones que el Usuario pueda tomar basado en esta información, así como por los posibles errores tipográficos que puedan contener los documentos y gráficos de la Página. La información está sometida a posibles cambios periódicos sin previo aviso de su contenido por ampliación, mejora, corrección o actualización de los Contenidos.
Notificaciones
Todas las notificaciones y comunicaciones por parte de UNICOOS al Usuario realizados por cualquier medio se considerarán eficaces a todos los efectos.
Disponibilidad de los Contenidos
La prestación del servicio de la Página y de los Contenidos tiene, en principio, duración indefinida. UNICOOS, no obstante, queda autorizada para dar por terminada o suspender la prestación del servicio de la Página y/o de cualquiera de los Contenidos en cualquier momento. Cuando ello sea razonablemente posible, UNICOOS advertirá previamente la terminación o suspensión de la Página.
Protección de Datos de Carácter Personal
UNICOOS es consciente de la importancia de la privacidad de los datos de carácter personal y por ello, ha implementado una política de tratamiento de datos orientada a proveer la máxima seguridad en el uso y recogida de los mismos, garantizando el cumplimiento de la normativa vigente en la materia y configurando dicha política como uno de los pilares básicos en las líneas de actuación de la entidad.
Durante la navegación a través de la web www.unicoos.com es posible se que soliciten datos de carácter personal a través de diferentes formularios dispuestos al efecto. Dichos datos formarán parte de los pertinentes ficheros en función de la finalidad determinada y concreta que motiva el recabo de los mismos.
De esta forma, la información particular de cada tratamiento de datos se aportará junto a cada formulario web, siendo común a todos ellos el responsable del fichero: UNICOOS EDUCATION, S.L. domiciliada en la calle Marqués de Cubas, 18, 28891 Velilla de San Antonio de Madrid, así como el lugar y forma de ejercicio de los derechos de acceso, rectificación, cancelación y oposición, que deberá formalizarse mediante una comunicación escrita a la dirección indicada anteriormente incluyendo copia del DNI o documento identificativo equivalente.
En el supuesto de que aporte sus datos a través de un mensaje de correo electrónico, el mismo formará parte de un fichero cuya finalidad será la gestión de la solicitud o comentario que nos realiza, siendo aplicables el resto de extremos indicados en el párrafo anterior.
Asimismo, las condiciones generales de contratación de los servicios de UNICOOS contienen las características y naturaleza del tratamiento de los datos que serán desarrollados por la misma en el supuesto de que contrate cualquiera de ellos.
Por otro lado, UNICOOS ha implantado las medidas técnicas y organizativas necesarias para evitar la pérdida, mal uso, alteración, acceso no autorizado y robo de los Datos Personales que los interesados pudieran facilitar como consecuencia del acceso a las diferentes secciones del website www.unicoos.com, aplicando las medidas de seguridad contempladas en el Real Decreto 1720/2007, de 21 de diciembre, por el que se aprueba el Reglamento de desarrollo de la Ley Orgánica 15/1999, de 13 de diciembre, de Protección de Datos de Carácter Personal.
Jurisdicción
Para cuantas cuestiones se susciten sobre la interpretación, aplicación y cumplimiento de este Aviso Legal, así como de las reclamaciones que puedan derivarse de su uso, todos las partes intervinientes se someten a los Jueces y Tribunales de Madrid, renunciando de forma expresa a cualquier otro fuero que pudiera corresponderles.
Legislación aplicable
El Aviso Legal se rige por la ley española.
Copyright © 2014 – UNICOOS EDUCATION S.L.
Reservados todos los derechos de autor por las leyes y tratados internacionales de propiedad intelectual. Queda expresamente prohibida su copia, reproducción o difusión, total o parcial, por cualquier medio.
 Hola unicoos,¿ puede hacer alguien el apartado A por el metodo de discos?
Hola unicoos,¿ puede hacer alguien el apartado A por el metodo de discos?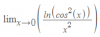 buenas tengo este limite y lo intente resolver por cambio de variable y no pude porque se me sigue complicando al momento de resolver.... alguien me puede ayudar por favor por cualquier metodo que no sea L Hopital.... necesito resolver el limite por cualquier metodo reduccion sustitucion o alguno que sea similar.... que no sea por L Hopital por favor
buenas tengo este limite y lo intente resolver por cambio de variable y no pude porque se me sigue complicando al momento de resolver.... alguien me puede ayudar por favor por cualquier metodo que no sea L Hopital.... necesito resolver el limite por cualquier metodo reduccion sustitucion o alguno que sea similar.... que no sea por L Hopital por favor