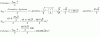-
buenas a ver si me podríais echar una manilla con esta integral,
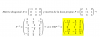
a^4xdx
gracias de ante mano.
saludos,
Antonio Silvio Palmitano
el 22/12/18Tienes la integral:
I = ∫ a4x*dx;
luego, escribes a la base de la potencia como una expresión exponencial con base natural, y queda:
I = ∫ (elna)4x*dx;
luego, aplicas la propiedad de una potencia cuya base es otra potencia, y queda:
I = ∫ e4lna*x*dx (*);
luego, planteas la sustitución (cambio de variable):
w = 4lna*x (1), de donde tienes:
dw = 4lna*dx, y de aquí tienes:
( 1/(4lna) )*dw = dx (2);
luego, sustituyes las expresiones señaladas (1) (2) en la integral señalada (*), y queda:
I = ∫ ew*( 1/(4lna) )*dw;
luego, extraes el factor constante, y queda:
I = ( 1/(4lna) )*∫ ew*dw;
luego, integras y queda:
I = ( 1/(4lna) )*ew + C;
luego, sustituyes la expresión señalada (1), y queda:
I = ( 1/(4lna) )*e4lna*x + C;
luego, expresas al factor exponencial como una potencia cuya base es otra potencia, y queda:
I = ( 1/(4lna) )*(elna)4x + C;
luego, resuelves la expresión exponencial (observa que tienes una composición entre funciones inversas evaluada), y queda:
I = ( 1/(4lna) )*a4x + C.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
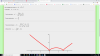
el 22/12/18Divides por 2 en el numerador y en el denominador del primer miembro de las ecuaciones cartesianas simétricas (o continuas) de la recta r, y queda:
(x+1/2)/1 = (y-0)/1 = (z-1)/3,
cuyo vector director (recuerda que tienes sus componentes en los denominadores) es:
u = < 1 , 1 , 3 >.
Tienes la ecuación vectorial paramétrica de la recta s, cuyo vector director es:
v = < 1 , 2 , 5 >.
Luego, como el plano buscado es paralelos a la recta r y a la recta s a la vez, puedes plantear que un vector normal a él es el producto vectorial entre los vectores directores de las rectas, y queda:
n = u x v, sustituyes las expresiones de los vectores directores, y queda:
n = < 1 , 1 , 3 > x < 1 , 2 , 5 >, resuelves el producto vectorial, y queda:
n = < -1 , -2 , 1 >.
Luego, tienes el punto Q(2,0,-1) que pertenece al plano, tienes la expresión del vector n = < -1 , -2 , 1 > que es un vector normal a él, por lo que planteas la ecuación vectorial del plano, y queda:
< -1 , -2 , 1 > • < x-2 , y-0 , z-(-1) > = 0, reduces expresiones en las componentes del segundo factor, y queda:
< -1 , -2 , 1 > • < x-2 , y , z+1 > = 0, desarrollas el producto escalar, y queda:
-1*(x-2) - 2y + 1*(z+1) = 0, distribuyes el primero y el tercer término, y queda:
-x + 2 - 2y + z + 1 = 0, reduces términos numéricos, y queda:
-x - 2y + z + 3 = 0, multiplicas en todos los términos de la ecuación por -1, y queda:
x + 2y - z - 3 = 0.
Espero haberte ayudado.
-
Buenos tardes,
Tengo una duda con una derivada que estoy haciendo os paso una imagen del ejercicio.
Gracias de antemano.
saludos,
Antonio Silvio Palmitano
el 22/12/18Vienes muy bien hasta tu segunda línea, que te ha quedado:
R = (1/2)*Ln(2x-1) - (1/2)*Ln(2x+1).
Luego, derivas término a término, y queda:
R ' = (1/2)*( 2/(2x-1) ) - (1/2)*( 2/(2x+1) ).
Luego, resuelves coeficientes en ambos miembros, y queda:
R ' = 1/(2x-1) - 1/(2x+1).
Espero haberte ayudado.
joshua Perez Peña
el 22/12/18Antonio Silvio Palmitano
el 23/12/18Así es, Joshua.
El resultado que te hemos mostrado corresponde a la expresión de la derivada de la función.
Luego, lo que has expresado tú al concluir tu desarrollo es el diferencial de la función:
dR = R ' (x) * dx,
sustituyes la expresión de la función derivada, y queda:
dR = ( 1/(2x-1) - 1/(2x+1) )*dx,
distribuyes en el segundo miembro, y queda:
dR = dx/(2x-1) - dx/(2x+1),
que es la expresión que tú has consignado.
Espero haberte ayudado.
-
Hola necesito ayuda para resolver este problema!
graciassss!!!
Un recipiente tiene forma de pirámide hexagonal. Si el lado del hexágono mide 4,5 dm y la altura de la pirámide es 10 dm, calcula la capacidad en centilitros y en litros del recipiente