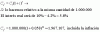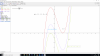
-
Ramon Maz
el 6/12/18Buenas, alguien sabria como resolver estos problemas? 1-Probar que 4x^5-2x^3-1=0 tiene exactamente dos soluciones reales .
2-Determina el numero de raices reales de 2x^3-3x^2-12x=m segun los valores de m
En el primero no se como demostrar que no hay ninguna mas, y en el segundo no consigo saber que valores de m tomar
-
Josefina Castro
el 6/12/18Me podrían guiar con este ejercicio
Decides depositar $1.000.000 en una cuenta de ahorros con 10% de interés por 12 años y la inflación esperada anual durante 12 años es de 4,2% anual. ¿Cuál es la cantidad de dinero que puede acumularse con el poder de compra de hoy?
-
Mariano Cornejo
el 6/12/18 -
Josefina Castro
el 6/12/18Hola
Me podrian ayudar con este ejercicio, debido que no me sale la operacion correcta.
Se ha invertido un capital de $2.000.000 a una tasa de interés anual de un 4,5% ¿En cuántos años se tendrán $2.500.000? ¿En cuántos años se tendrán $3.500.000?
Muchas Gracias
-
Junior Stalin
el 6/12/18- ∛x + ∛y² ⁄ ∛x² + ∛y4 - ∛xy²
- Me podrían Ayudar con esta racionalización por favor :( llego a un punto que ya no se que mas sigue :/
Antonio Silvio Palmitano
el 6/12/18Vamos con una orientación.
Puedes llamar:
∛(x) = u, de donde tienes: ∛(x2) = ( ∛(x) )2 = u2;
∛(y2) = v, de donde tienes: ∛(y4) = ( ∛(y2) )2 = v2;
y también tienes: ∛(x*y2) = ∛(x)*∛(y2) = u*v.
Luego, sustituyes todas las expresiones finales remarcadas en la expresión de tu enunciado, y queda:
(u + v) / (u2 + v2 - u*v) =
multiplicas por (u + v) en el numerador y en el denominador, y queda:
= (u + v)*(u + v) / (u2 + v2 - u*v)*(u + v) =
expresas al numerador como una potencia, distribuyes en el denominador, y queda:
= (u + v)2 / (u3 + u2*v + v2*u + v3 - u2*v - u*v2) =
cancelas términos opuestos en el denominador, y queda:
= (u + v)2 / (u3 + v3) =
sustituyes las expresiones originales de u y de v, y queda:
= ( ∛(x) + ∛(y2) )2 / ( ( ∛(x) )3 + ( ∛(y2) )3 ) =
simplificas índices y exponentes cúbicos en ambos términos del denominador, y queda:
= ( ∛(x) + ∛(y2) )2 / ( x + y2 ).
Espero haberte ayudado.
-
Carlos
el 6/12/18Me podeis ayudar con estos 2 ejercicios que no sé resolverlos
También quería ponerlos en la recta y saber como y donde poner los signos + o -
Antonio Silvio Palmitano
el 6/12/181)
Tienes una ecuación polinómica cuadrática de la forma: A*x2 + B*x + C = 0,
cuyos coeficientes son:
A = 1, B = a, C = a;
luego, planteas la expresión de su discriminante, y queda:
D = B2 - 4*A*C, sustituyes las expresiones de los coeficientes, y queda:
D = a2 - 4*1*a, resuelves el segundo término, y queda:
D = a2 - 4*a (1).
Luego, recuerda que para que la ecuación polinómica cuadrática tenga dos soluciones reales distintas debe cumplirse:
D > 0, sustituyes la expresión señalada (1), y queda:
a2 - 4*a > 0, sumas 4 en ambos miembros, y queda:
a2 - 4*a + 4 > 4, factorizas el trinomio cuadrado perfecto en el primer miembro, y queda:
(a - 2)2 > 4, extraes raíz cuadrada en ambos miembros (observa que el índice es par, y queda:
|a - 2| > 2;
luego, por propiedad del valor absoluto, tienes dos opciones:
a)
a - 2 > 2, aquí sumas 2 en ambos miembros, y queda:
a > 4,
b)
-(a - 2) > 2, aquí distribuyes el primer miembro, y queda:
-a + 2 > 2, aquí restas 2 en ambos miembros, y queda:
-a > 0, aquí multiplicas por -1 en ambos miembros (observa que cambia la desigualdad), y queda:
a < 0.
Luego, puedes concluir que la ecuación polinómica cuadrática de tu enunciado tendrá dos soluciones reales distintas para todo número real a que sea estrictamente mayor que cuatro o estrictamente menor que cero.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 6/12/181)
Tienes una ecuación polinómica cuadrática de la forma: A*x2 + B*x + C = 0,
cuyos coeficientes son:
A = k2, B = -3, C = 4 (observa que k debe ser distinto de cero);
luego, planteas la expresión de su discriminante, y queda:
D = B2 - 4*A*C, sustituyes las expresiones de los coeficientes, y queda:
D = (-3)2 - 4*k2*4, resuelves los términos, y queda:
D = 9 - 16*k2 (1).
Luego, recuerda que para que la ecuación polinómica cuadrática no tenga soluciones reales debe cumplirse:
D < 0, sustituyes la expresión señalada (1), y queda:
9 - 16*k2 < 0, restas 9 en ambos miembros, y queda:
-16*k2 < -9, divides por -16 en ambos miembros (observa que cambia la desigualdad), y queda:
k2 > 9/16, extraes raíz cuadrada en ambos miembros (observa que el índice es par), y queda:
|k| > 3/4;
luego, por propiedad del valor absoluto, tienes dos opciones:
a)
k > 3/4,
b)
-k > 3/4, aquí multiplicas por -1 en ambos miembros (observa que cambia la desigualdad), y queda:
k < -3/4.
Luego, puedes concluir que la ecuación polinómica cuadrática de tu enunciado no tendrá dos soluciones reales para todo número real k que sea estrictamente menor que -3/4 o estrictamente mayor que 3/4.
Espero haberte ayudado.
-
Armando Fiorini
el 6/12/18
Se que no es lo que debo hacer, pero ya he intentado resolverlo por todas partes y no logro con el camino correcto, disculpen las molestias si alguien me puede ayudar con este ejercicio le agradeceria mucho : Diseñe un sumador completo de cuatro bits utilizando un (1) decodificador de 2x4 y todos los decodificadores 3x8 necesarios para completar el circuito. Gracias de antemano
-
Sergi Raga Estruch
el 6/12/18 -
comando bachuerino
el 6/12/18 -
Noora
el 6/12/18
