-
Tengo este binomio de Newton (que en general me salen) pero este no hay manera si alguien me ayudara lo mas rápido posible por favor y me explicase su razonamiento
(2x-3y²)5
Antonio Silvio Palmitano
el 7/12/18Recuerda la expresión del desarrollo de un binomio:
(a + b)n = ∑(k=0,n) C(n,k)*an-k*bk (1).
Luego, observa la expresión que tienes en tu enunciado, y a su vez tienes los datos:
a = 2*x,
b = -3*y2 = -1*3*y2,
n = 5.
Luego, planteas las expresiones de los factores que tienes en el argumento de la sumatoria señalada (1), sustituyes las expresiones de los datos, y quedan:
C(n,k) = C(5,k) (2),
an-k = (2*x)5-k = 25-k*x5-k (3),
bk = (-1*3*y2)k = (-1)k*3k*(y2)k = (-1)k*3k*y4k (4).
Luego, sustituyes los datos y sustituyes las expresiones señaladas (2) (3) (4) en la ecuación señalada (1), y queda:
(2*x - 3*y2)5 = ∑(k=0,5) C(5,k)*25-k*x5-k*(-1)k*3k*y4k = ∑(k=0,5) C(5,k)*(-1)k*25-k*3k*x5-k*y4k,
que es la expresión del desarrollo del binomio de tu enunciado como una suma de seis términos, numerados de cero a cinco.
Luego, solo que da que reemplaces valores y tendrás la expresión del desarrollo completo.
Espero haberte ayudado.
-
 hola buenas tengo dudas sobre este ejercicio, las soluciones me salen: a) √8
hola buenas tengo dudas sobre este ejercicio, las soluciones me salen: a) √8b)π:-2y+2z=0
c) D=(0,2,2)
Antonio Silvio Palmitano
el 7/12/18Comenzamos con el último inciso.
c)
Tienes tres vértices consecutivos, agregas el cuarto vértice, y quedan:
A(1,1,1), B(2,2,2), C(1,3,3) y D(a,b,c).
Luego (haz un dibujo tentativo para ver mejor la situación), puedes plantear las ecuación vectorial:
AB + AD = AC, restas AB en ambos miembros, y queda:
AD = AC - AB, sustituyes las expresiones de los vectores, y queda:
< a-1 , b-1 , c-1 > = < 1-1 , 3-1 , 3-1 > - < 2-1 , 2-1 , 2-1 >, resuelves operaciones numéricas, y queda:
< a-1 , b-1 , c-1 > = < 0 , 2 , 2 > - < 1 , 1 , 1 >, resuelves el segundo miembro:
< a-1 , b-1 , c-1 > = < -1 , 1 , 1 >;
luego, por igualdad entre vectores, igualas componente a componente, y tienes el sistema de ecuaciones:
a - 1 = -1, aquí sumas 1 en ambos miembros, y queda: a = 0,
b - 1 = 1, aquí sumas 1 en ambos miembros, y queda: b = 2,
c - 1 = 1, aquí sumas 1 en ambos miembros, y queda: c = 2;
luego, tienes que la expresión del cuarto vértice es:
D(0,2,2).
Planteas el producto vectorial entre los vectores BA y BC, y tienes que un vector perpendicular al plano que contiene al paralelogramo (observa que sustituimos las expresiones de los vectores y que resolvemos el producto vectorial):
n = BA x BC, sustituyes las expresiones de los vectores, y queda:
n = < -1 , -1 , -1 > x < -1 , 1 , 1 >, resuelves el producto vectorial (te dejo la tarea del desarrollo),
n = < 0 , 2 , -2 >.
a)
Recuerda que el módulo del producto vectorial es igual al área del paralelogramo determinado por los dos vectores, por lo que puedes plantear
Ap = |BA x BC| = |n| = |< 0 , 2 , -2 >| = √( 02+22+(-2)2 ) = √(8).
b)
Con el vector n = < 0 , 2 , -2 > y uno de los vértices del paralelogramo ( observa que elegimos el vértice A(1,1,1) ), puedes plantear la ecuación vectorial del plano que contiene al paralelogramo, y queda:
< 0 , 2 , -2 > • < x-1 , y-1 , z-1 > = 0, desarrollas el producto escalar en el primer miembro, y queda:
0*(x-1) + 2*(y-1) - 2*(z-1) = 0, cancelas el término nulo, distribuyes en los demás términos, y queda:
2*y - 2 - 2*z + 2 = 0, cancelas términos opuestos, divides por 2 en todos los términos de la ecuación, y queda:
y - z = 0.
Espero haberte ayudado.
-
Hola quisiera que por favor me ayuden con este ejercicio, de antemano muchas gracias.
Plantee el calculo de la longitud del arco de curva C que se extiende desde A(3,0,3) hasta B(0,1,2) en el primer octante.
C: ((x²)/9) + y² = 1
z + y =3
Antonius Benedictus
el 7/12/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Marcos
el 7/12/18Me he quedado igual. Disculpa. No entiendo ni siendo PRO, ni teniendo una versión PREMIUM, se me puede responder a una pregunta clara. Ese video que me has mandado no sé si se ha equivocado, pero me resulta chino, lo he visto. Para nada he visto eso en clase. Simplemente en las dos hojas tengo una matriz, y he preguntado si (resta y demás) entre lineas es correcta, para llegar al rango que he llegado. Lo siento, por ser tan claro, pero no entiendo la funcionalidad del foro. Yo ni he dicho que me lo hagan ni nada. Lo tengo hecho, y no sé si estará bien el rango. Sólo he preguntado eso. Si los cambios son correctos.
Antonio Silvio Palmitano
el 7/12/18Por lo que puedo apreciar, has resuelto bien el ejercicio que muestras en tu primera imagen.
En la segunda imagen, tienes la matriz ampliada del sistema:
1 1 2
1 -1 4
0 1 5.
A la fila 2 le restas la fila 1, y queda:
1 1 2
0 -2 2
0 1 5.
Permutas la fila 2 con la fila 3, y queda:
1 1 2
0 1 5
0 -2 2.
A la fila 1 le restas la fila 2, a la fila 3 le sumas el doble de la fila 2, y queda:
1 0 -3
0 1 5
0 0 12.
Luego, puedes apreciar que el rango de la matriz del sistema es dos, y que el rango de la matriz ampliada es 3, por lo que puedes concluir que el sistema es incompatible.
Espero haberte ayudado.
-
HICE UNA PREGUNTA DESDE MI USUARIO HACE UNAS HORAS Y AL QUERER VER LA RESPUESTA DE ANTONIO ME SALIO ESO , ADEMAS DE NO PODER VER NADA NI PUNTUAR NI COMENTAR , NO ME DEJA HACER NINGUNA OTRA PREGUNTA , NO SE QUE SUCEDIO .
LA AYUDA QUE PEDI FUE CON ESTE EJERCICIO :
|
|
|
V
César
el 7/12/18César
el 7/12/18Diego Raso
el 7/12/18 -
Buenas, tengo el ejercicio siguiente resuelto, pero no entiendo como se llega a dicha conclusión, ¿alguien me lo puede explicar? Muchísimas gracias.
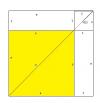
LA DIAGONAL DEL CUADRADO. ¿En qué porcentaje aumenta la diagonal de un
cuadrado cuando su lado, de medida a, aumenta en una unidad? Representación gráfica.
p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; font: 12.0px Helvetica}
- 100/a
Antonio Silvio Palmitano
el 6/12/18Planteas la expresión de la longitud de la diagonal del cuadrado inicial (D0) en función de la longitud de su lado (a), y queda:
D0 = √(2)*a (1).
Planteas la expresión de la longitud de la diagonal del cuadrado inicial (D1) en función de la longitud de su lado (a+1), y queda:
D1 = √(2)*(a+1) (2).
Luego, planteas la expresión de la variación de la longitud de la diagonal, y queda:
ΔD = D1 - D0,
sustituyes las expresiones señaladas (2) (1), y queda:
ΔD = √(2)*(a+1) - √(2)*a,
extraes factor común, y queda:
ΔD = √(2)*(a+1 - a),
cancelas términos opuestos en el agrupamiento, resuelves, y queda:
ΔD = √(2) (3),
que es el valor del incremento de la longitud de la diagonal del cuadrado;
luego, planteas la expresión del incremento relativo de la longitud de la diagonal del cuadrado, y queda:
ΔDr = ΔD / D0,
sustituyes las expresiones señaladas (3) (1), y queda:
ΔDr = √(2) / √(2)*a,
simplificas el segundo miembro, y queda:
ΔDr = 1/a (4),
que es la expresión del incremento relativo de la longitud de la diagonal del cuadrado;
luego, planteas la expresión del incremento relativo porcentual, y queda:
ΔDp = ΔDr*100,
sustituyes la expresión señalada (4) en el segundo miembro, y queda:
ΔDp = (1/a)*100,
resuelves el segundo miembro, y queda:
ΔDp = 100/a,
que es la expresión del incremento relativo porcentual de la longitud de la diagonal del cuadrado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 6/12/18Observa que los triángulos MAN y BAC tienen:
que el ángulo  es común a ambos triángulos;
que la longitud del lado MA es igual a la mitad de la longitud del lado BA,
que la longitud del lado NA es igual a la mitad del la longitud del lado CA;
por lo que tienes que los triángulos MAN y BAC son semejantes,
por lo que puedes concluir que la longitud del lado MN es igual a la mitad de la longitud del lado BC:
|MA|/|BA|= a/(2a) = 1/2,
|NA|/|CA| = b/(2b) = 1/2,
y por lo tanto tienes:
|MN|/|BC| = x/y = 1/2,
multiplicas por y en ambos miembros de la igualdad remarcada, y queda:
x = (1/2)y.
Espero haberte ayudado.
-
Hola, estaba tratando de resolver el siguiente problema pero no se por donde tomarlo, agradecería cualquier sugerencia:
Hallar el radio R de la mínima circunferencia que contenga a n circunferencias de radio r, en donde la disposición entre circunferencias es que cualquiera que no esté en la frontera tiene 6 circunferencias adyacentes.
Muchas gracias de antemanoDavid
el 12/12/18Lamento de todo corazon no poder ayudarte, pero unicoos (por ahora) solo llega hasta bachiller con matemáticas, física y química. Tu duda se da en la "uni". Espero lo entiendas... Como a veces hago alguna excepción y además hay muchos enlaces de teoría y ejercicios resueltos, te recomiendo le eches un vistazo a la seccion MATEMATICAS, UNIVERSIDAD de la web