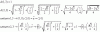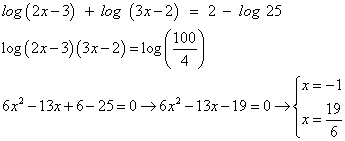-
Antonio
el 19/11/18f(x)=2x3+12x2+ax+b
f(x)'=6x2+24x+a
f(x)''=12x+24
El punto de inflexión cumple que f''(x)=0
12x+24=0 =>x=-2 El punto de inflexión es (-2,q) donde q=f(-2)=y(-2)
La pendiente de la recta tangente en ese punto es m=f'(-2)
m=2 pues la recta es y=2x-3
f'(-2)=a-24
igualando
a-24=2=>a=26
calculamos ahora la q, para ello:
f(-2)=b-20
y(-2)=-7
igualando:
b-20=-7=>b=13
-
Buenas tardes,
Nueva duda combinatoria:
Con las letras b,c,d,e,f,g,h,i,j,k,l,m,n,o (14)
¿cuantas palabras de 14 letras empiezan y terminan por vocal?
Gracias.
David
el 12/12/18Que empiecen por "e" y terminen por "i", seríam variaciones sin repeticion de 12 elementos tomados de 12 en 12... V12,12.
Las mismas para las que empiezan por "i" y terminan por "e"... O del tipo e...........o, o..........e, i..........o, o.........i
Como son 6 diferentes posibilidades ... El resultado final 6 x V12,12...
Piensa, lucha, pregunta.. Un abrazo! -
Dudas ejercicio:
¿Cuantos números de 5 cifras sin repeticiones se pueden formar con los dígitos 2,4,5,6,7 y 8 que sean múltiplos de 3?
¿Cuantos números de 5 cifras sin repeticiones se pueden formar con los dígitos 2,4,5,6,7,y 8 que contienen al 4 y al 6?
Gracias.
David
el 12/12/18Para que un numero sea multiplo de 3, la suma de sus cifras debe ser multiplo de 3... Es el caso de todas las variaciones posibles, por ejemplo, con los números 2,4,5,6,7, que suman 24 o con los numeros 4,5,6,7,8 que suman 30...
Para cada una de ellas (deberás comprobar en cuantos casos se cumple que la suma es multiplo de 3) las opciones posibles serán V5,5... Multiplica el numero de diferentes opciones por V5,5
En el segundo, las que contienen un 4 en primer lugar serán V5,4. Las que cotienen un 4 en segunda posicion serán V5,4... Y asi en cinco posiciones diferentes. Por tanto, todas los numeros que contienen un 4 serán 5 x V5,4
Lo mismo para los que contienen un 6... 5 x V5,4......
El resultado final 10 x V5,4
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
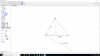
Antonio Silvio Palmitano
el 19/11/18Tienes que la longitud del lado del cuadrado es: 10, y tienes que los lados AB y CD son paralelos al vector: v = <3,4,0>.
Vamos por etapas:
1°)
Luego, observa que el vértice C queda expresado (observa que el segmento AC es paralelo al eje OZ): C(-2,1,6-10),
resuelves la tercera coordenada, y queda: C(-2,1,-4).
2°)
Planteas la expresión del segundo vértice superior, y queda: B(x,y,6) (observa que el segmento |AB| es paralelo al plano OXY);
luego, planteas la expresión del vector determinado por los dos vértices superiores, y queda:
AB = < x-(-2) , y-1 , 6-6 >, resuelves componentes, y queda: AB = < x+2 , y-1 , 0 > (1).
3°)
Planteas la expresión del segundo vértice inferior (observa que el segmento |BD| es paralelo al eje OZ, y que la longitud de dicho segmento es igual al lado del cuadrado), y queda: D(x,y,6-10), resuelves la tercera coordenada, y queda: D(x,y,-4);
luego, planteas la expresión del vector determinado por los dos vértices inferiores, y queda:
BD = < x-(-2) , y-1 , -4-(-4) >, resuelves componentes, y queda: BD = < x+2 , y-1 , 0 > (2).
4°)
Observa que las expresiones de los vectores AB y CD coinciden, y esto se debe a que son paralelos y sus módulos son iguales;
luego, observa que sus módulos son iguales a la longitud del lado del cuadrado, por lo que puedes plantear la ecuación:
|AB| = 10 (o si prefieres: |BD| = 10),
sustituyes la expresión del módulo del vector AB en el primer miembro, y queda:
√( (x+2)2 + (y-1)2 + (0)2 ) = 10, elevas al cuadrado en ambos miembros, cancelas el término nulo, y queda:
(x + 2)2 + (y - 1)2 = 100 (3).
5°)
Como tienes en tu enunciado que el vector AB (o si prefieres, el vector CD) es paralelo al vector v, puedes plantear que el vector AB es un múltiplo escalar del vector v, y tienes la ecuación vectorial:
AB = k*v, con k ∈ R y k > 0 (observa que los vectores tienen igual sentido), sustituyes las expresiones de los vectores, y queda:
< x+2 , y-1 , 0 > = k*< 4 , 3 , 0 >, resuelves el producto en el segundo miembro, y queda:
< x+2 , y-1 , 0 > = < 4k , 3k , 0 >;
luego, por igualdad entre vectores, tienes las ecuaciones:
x + 2 = 4k, aquí restas 2 en ambos miembros, y queda: x = 4k - 2 (4),
y - 1 = 3k, aquí sumas 1 en ambos miembros, y queda: y = 3k + 1 (5).
6°)
Sustituyes las expresiones señaladas (4) (5) en la ecuación señalada (3), y queda:
(4k-2 + 2)2 + (3k+1 - 1)2 = 100, cancelas términos opuestos en los agrupamientos, y queda:
(4k)2 + (3k)2 = 100, resuelves términos, y queda:
16k2 + 9k2 = 100, reduces términos semejantes, y queda:
25k2 = 100, divides por 25 en ambos miembros, y queda:
k2 = 4, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda: k = 2 (6).
7°)
Reemplazas el valor señalado (6) en las ecuaciones señaladas (4) (5), resuelves, y queda: x = 6, y = 7.
8°)
Remplazas los valores remarcados en las expresiones de los vértices que tienes remarcadas en los desarrollos de la segunda y de la tercera etapa, y queda:
B(6,7,6) y D(6,7,-4).
Luego, tienes que los vértices del cuadrado son: A(-2,1,6), B(6,7,6), C(-2,1,-4) y D(6,7,-4).
9°)
Planteas las expresiones de los vectores que te indican en el inciso (b) de tu enunciado, y queda:
BC = < -2-6 , 1-7 , -4-6 >, resuelves componentes, y queda: BC = < -8 , -6 , -10 > (7),
CD = < 6-(-2) , 7-1 , -4-(-4) >, resuelves componentes, y queda: CD = < 8 , 6 , 0 > (8), cuyo módulo es: |CD| = 10 (9);
luego, planteas la expresión del vector unitario asociado al vector CD, y queda:
u = CD/|CD|, reemplazas las expresiones señaladas (8) (9), y queda:
u = < 8 , 6 , 0 >/10, resuelves, y queda:
u = < 4/5 , 3/5 , 0 > (10);
luego, planteas la expresión de la proyección escalar del vector BC sobre la dirección determinada por el vector unitario asociado al vector CD, y queda:
ProyECD(BC) = BC•u, sustituyes las expresiones de los vectores en el segundo miembro, y queda:
ProyECD(BC) = < -8 , -6 , -10 >•< 4/5 , 3/5 , 0 >, desarrollas el producto escalar, y queda:
ProyECD(BC) = -8*(4/5) - 6*(3/5) - 10*0, resuelves, y queda:
ProyECD(BC) = -10 (11);
luego, multiplicas al valor señalado (11) por la expresión del vector unitario asociado a CD, y la expresión vectorial de dicha proyección queda:
ProyVCD(BC) = -10*< 4/5 , 3/5 , 0 >, resuelves, y queda:
ProyVCD(BC) = < -8 , -6 , 0 >.
Espero haberte ayudado.