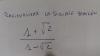sec = 1/cos

g(x) = 3sec(x) = 3/cos(x)

cos(x) = 0 en x = π/2 + nπ,  con n entero. (Una raíz mas n "medias vueltas". 0 medias vueltas, y las medias vueltas negativas también valen).

De modo que 3/cos(x) tiene asíntotas verticales en x = π/2 + nπ,  con n ∈ ℤ

Asíntotas horizontales no tiene.

Pon foto del enunciado original.

Revisa operaciones: 

Muchas gracias Antonio, me quedó claro. Pero en la última parte, por qué las derivadas parciales se igualan a cero? Esa parte aún no la comprendo bien. Muchas gracias.

Recuerda que una condición necesaria para la existencia de mínimo o máximo de una función de dos variables, continua con derivadas parciales primeras continuas, es que las dos derivadas parciales sean iguales a cero.

Espero haberte ayudado.

Intervalo (-2, 1)                => Respuesta c

Desigualdad 0 ≤ x ≤ 3     => Respuesta b

Desigualdad -5 ≤ x < -4   => Respuesta d

Intervalo [0, + ∞)              => Respuesta a

Desigualdad x ≤ -1          => Respuesta e

a)

Puedes plantear que todo polinomio del conjunto P₂(x) puede escribirse como combinación lineal de los elementos de la familia finita T:

α*1 + β*x + γ*x² = a₀*x² + a₁*x + a₂, 

con α, β y γ números reales o complejos, según corresponda, que debes determinar para cada elemento del conjunto P₂(x);

luego, restas a₀*x², a₁*x y a₂ en ambos miembros, ordenas términos (observa que queda el polinomio nulo en el segundo miembro), y queda:

α*1 - a₂ + β*x - a₁*x + γ*x² - a₀*x² = 0*x² + 0*x + 0, extraes factores comunes por grupos de dos términos en el primer miembro, y queda:

(α - a₂)*1+ (β - a₁)*x+ (γ - a₀)*x² = 0*x² + 0*x + 0;

luego, por igualdad entre expresiones polinómicas, igualas los coeficientes de los términos de igual grado, y queda el sistema de ecuaciones:

α - a₂ = 0, de donde puedes despejar: α = a₂,

β - a₁ = 0, de donde puedes despejar: β = a₁,

γ - a₀ = 0, de donde puedes despejar: γ = a₀.

b)

Luego, para probar que los elementos del conjunto T son linealmente independientes, planteas la "combinación lineal nula", y queda:

A*1 + B*x + C*x² = 0*x² + 0*x + 0, 

con A, B y C números reales o complejos, según corresponda, que debes determinar:

luego, por igualdad entre expresiones polinómicas, igualas los coeficientes de los términos de igual grado, y queda el sistema de ecuaciones:

A = 0,

B = 0, 

C = 0,

por lo que tienes que los elementos del conjunto generador T son linealmente independientes, por lo que T es una base de P₂(x).

c)

Como la base T tiene tres elementos, puedes concluir que la dimensión de P₂(x) es 3.

Espero haberte ayudado.

César. Muchísimas gracias. Acabo de aprender algo nuevo.