-
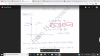
En un ejercicio en el que me pide calcule la diferencia de potencial en campos electricos, alguien me puede explicar por que se pasa de lo que os he rodeado al segundo circulo que os he hecho,
Antonio Silvio Palmitano
el 16/1/19Has planteado bien la expresión del potencial resultante en el punto B:
V = k*(q1/r1 + q2/r2) (1).
Luego, tienes lo datos:
k = 9*109 N*m2/C2 (2) (constante de Coulomb),
q1 = 40 nC = 40*10-9 C (3), ubicada en el punto: A'(1,0) (en cm), que es equivalente a: A'(10-2,0) (en metros),
q2 = -10 nC = -10*10-9 C (4), ubicada en el punto: A(0,2) (en cm), que es equivalente a: A'(0,2*10-2) (en metros).
Luego, tienes el punto en estudio: B(1,2) (en cm), que es equivalente a: B(10-2,2*10-2) (en metros),
por lo que tienes que las expresiones de las distancias entre el punto en estudio y los puntos donde están ubicadas las cargas quedan:
r1 = |AB| = 2 cm = 2*10-2 m (5),
r2 = |A'B| = 1 cm = 10-2 m (6).
Luego, reemplazas los valores señalados (5) (6) en la expresión señalada (1), y queda:
V = k*( q1/(2*10-2) + q2/(10-2) ),
aquí aplicas la propiedad de las potencias con exponente negativo (recuerda: 1/10-n = 10n), y queda:
V = k*( q1*102/2 + 102*q2 ),
resuelves potencias, y queda:
V = k*( q1*100/2 + 100*q2 ),
resuelves el coeficiente y ordenas factores en el primer término del agrupamiento, y queda:
V = k*( 50*q1 + 100*q2 ).
Espero haberte ayudado.
-
Desde un avión se lanza una granada en dirección horizontal con una velocidad de 100 m/s. La granada estalla a los 20 s de haber sido lanzada, dividiéndose en dos trozos, de masas 1 kg y 1,5 kg. El fragmento mayor sale despedido según la dirección horizontal con una velocidad de 250 m/s. Calcular la velocidad y dirección del otro fragmento.
¿Cómo se puede saber en qué dirección sale despedido el otro fragmento? Hago un dibujo y no lo veo nada claro
Antonio Silvio Palmitano
el 16/1/19Establece un sistema de referencia con instante inicial: ti = 0 correspondiente al lanzamiento de la granada, con origen en la posición del avión en dicho instante, con eje OX horizontal con sentido positivo acorde al desplazamiento del avión, y con eje OY vertical con sentido positivo hacia arriba.
Luego, tienes los datos iniciales:
M = 2,5 Kg (masa de la granada),
xi = 0, yi = 0 (posición inicial de la granada),
vxi = 100 m/s, vyi = 0 (velocidad inicial de la granada, observa que conserva la velocidad del avión),
a = -g = -9,8 m/s2 (aceleración gravitatoria terrestre, con dirección vertical y sentido hacia abajo);
luego, planteas las expresiones de las funciones de posición y de velocidad de Tiro Oblicuo (o Parabólico), cancelas términos nulos, resuelves coeficientes, y queda:
x = 100*t,
y = -4,9*t2,
vx = 100,
vy = -9,8*t;
luego, evalúas las cuatro expresiones para el instante en estudio: t = 20 s (observa que es el instante inmediato anterior al estallido de la granada), resuelves, y queda:
x = 2000 m (abscisa del punto donde ocurre la explosión),
y = -1960 m (ordenada del punto donde ocurre la explosión),
vx = 100 m/s (componente horizontal de la velocidad de la granada antes de la explosión),
vy = -196 m/s (componente vertical de la velocidad de la granada antes de la explosión);
luego, planteas las expresiones de las componentes del impulso de la granada inmediatamente antes del estallido, y queda:
pAx = M*vx,
pAy = M*vy,
reemplazas el valor de la masa de la granada y los valores de las componentes de su velocidad, y queda:
pAx = 2,5*100 = 250 N*s (1),
pAy = 2,5*(-196) = -490 N*s (2).
Luego, tienes los datos correspondientes al instante inmediato posterior al estallido (t = 20 s):
para el trozo mayor:
M1 = 1,5 Kg,
v1x = 250 m/s,
v1y = 0.
para el trozo menor:
M2 = 1 Kg,
v2x = a determinar,
v2y = a determinar;
luego, planteas las expresiones de las componentes del impulso del sistema formado por los dos trozos de la granada inmediatamente después del estallido, y queda:
pDx = M1*v1x + M2*v2x,
pDy = M1*v1y + M2*v2y,
reemplazas los valores de las masas de los trozos de la granada y los valores de las componentes de sus velocidades, y queda:
pDx = 1,5*250 + 1*v2x,
pDy = 1,5*0 + 1*v2y,
resuelves términos, cancelas el término nulo, y queda:
pDx = 375 + 1*v2x (3),
pDy = 1*v2y (4).
Luego, si consideras que la diferencia entre el instante inmediato anterior y el instante inmediatamente posterior al estallido es prácticamente nula, puedes plantear conservación del impulso, y tienes el sistema de ecuaciones:
pDx = pAx,
pDy = pAy,
sustituyes la expresión señalada (3) y el valor señalado (1) en la primera ecuación, sustituyes la expresión señalada (4) y el valor señalado (2) en la segunda ecuación, y queda:
375 + 1*v2x = 250, de aquí despejas: v2x = -125 m/s,
1*v2y = -490, de aquí despejas: v2y = -490 m/s;
por lo que puedes concluir que el fragmento más pequeño se desplaza con sentido horizontal opuesto al fragmento más grande, y con sentido vertical hacia abajo;
luego, planteas la expresión del módulo de la velocidad del trozo más pequeño, y queda:
v = √(v2x2 + v2y2) = √( (-125)2 + (-490)2 ) = √(255725) ≅ 505,693 m/s;
luego, planteas la expresión de la tangente de su ángulo de inclinación con respecto a la dirección del avión, y queda:
tanθ = v2y/v2x = -490/(-125) = 3,92,
luego, compones con la función inversa de la tangente (haz un diagrama de velocidades, y presta atención al cuadrante en que se encuentra la velocidad del fragmento menor), y queda:
θ = arctan(3,92) ≅ 75,689° + 180° ≅ 255,689°.
Espero haberte ayudado.
-
Raúl RC
el 16/1/19Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato. Espero algun otro unico universitario pueda ayudarte, lo ideal sería que os ayudárais los unos a los otros
Como excepción el profe grabó unos vídeos que espero puedan servirte, lamento no poder ayudarte mas
Momento de inercia -
Fernando Alfaro
el 16/1/19Ej 13.76
1 pie = 12 pulgadas y 1 pulgada = 2.54 cm
g = -9.8 m/s2 * 100cm/m * pulgadas/2.54cm * pies/12 pulgadas = -9.8*100/(2.54*12) = -32.152 pies/s2
Origen de coordenadas en el punto de partida => x0 = 0 e y0 = 0
Paramétricas del proyectil:
x(t) = v0cos(θ)t => t(x) = x/v0cos(θ)
y(t) = ½gt2 + v0sen(θ)t
Trayectoria del proyectil, haciendo y(t(x)):
y(t(x)) = ½g(x/v0cos(θ))2 + v0sen(θ)(x/v0cos(θ)) => y(x) = gx2 /(2v02 cos(θ)2) + tg(θ)x
Despejando v0 :
y(x) - tg(θ)x = gx2 /(2v02 cos(θ)2) => 2v02 cos(θ)2 = gx2 / (y(x) - tg(θ)x) => v02 = gx2 / (2cos(θ)2(y(x) - tg(θ)x)) => v0 = √(gx2 / (2cos(θ)2(y(x) - tg(θ)x)))
y(x) valdría 3 pies tanto para x = 27 pies como para x = 33 pies. Sustituyendo valores:
Para x = 27 => v0 = √(-32.15(27)2 / (2cos(50)2(3 - tg(50)*27))) = 31.18 fps (feet per second = pies/segundo)
Para x = 33 => v0 = √(-32.15(33)2 / (2cos(50)2(3 - tg(50)*33))) = 34.15 fps
Entonces el rango de velocidades para que aterrice a (no mas de) 3 pies del hoyo es: 31.18 fps ≤ v0 ≤ 34.15 fps
Luego si quieres puedes pasarlo a m/s. O convertir los pies a metros y trabajarlo todo en el sistema MKS.
(Se colgó la conexión y lo tuve que transcribir todo de nuevo, revisa las cuentas por las dudas).
Si no se entendió algún paso avisa.
-
Antonio Silvio Palmitano
el 15/1/19Observa que en el punto más alto actúan dos fuerzas sobre la persona, ambas con dirección vertical:
su Peso, con sentido hacia abajo,
la acción normal de la pared cilíndrica de la rueda, con sentido hacia abajo;
luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
P + N = M*acp;
luego, si consideras la situación crítica donde el contacto entre la persona y la pared cilíndrica de la rueda es casi imperceptible, aquí tienes que la acción normal es nula, por lo que cancelas el segundo término de la ecuación, y ésta queda:
P = M*acp, sustituyes la expresión del módulo del peso, y queda:
M*g = M*acp, divides por M en ambos miembros, y queda:
g = acp,
por lo que tienes que la persona "no cae" porque su peso aporta la fuerza centrípeta de giro, y observa que tienes que la aceleración centrípeta es igual a la aceleración gravitatoria terrestre.
Espero haberte ayudado.
-
Hola buenas, tan solo quería estar completamente seguro de que este ejercicio está bien. La razón por la que dudo es porque es muy simple. Gracias.


Antonio Silvio Palmitano
el 15/1/19Has planteado correctamente la expresión del módulo de la aceleración tangencial, pero observa que debes corregir al reemplazar el valor del módulo de la velocidad tangencial inicial (consideramos :
aT = Δv/Δt = (vf - vi)/(tf - ti) = (15 - 14,5)/(0,5 - 0) = 0,5/0,5 = 1 m/s2.
Luego, planteas la expresión del módulo de la aceleración centrípeta (observa que no es constante) en el instante final (observa que en tu enunciado dicen: "... su velocidad ha pasado de..."), y queda:
acp = vf2/R = 152/30 = 7,5 m/s2.
Luego, planteas la expresión del módulo de la aceleración resultante, y queda:
a = √(aT2 + acp2) = √(12 + 7,52) = √(1 + 56,25) = √(57,25) m/s2 ≅ 7,566 m/s2.
Espero haberte ayudado.
-
 A ver que me estoy liando mucho. La v no seria w×r? De donde sale que la velocidad lineal es 1.57? Gracias únicos
A ver que me estoy liando mucho. La v no seria w×r? De donde sale que la velocidad lineal es 1.57? Gracias únicos
Antonio Silvio Palmitano
el 15/1/19Observa que la única fuerza horizontal que está aplicada sobre el cuerpo que gira es la tensión de la cuerda que lo une al poste, que es el eje de giros (observa que las otras fuerzas son el Peso y la acción normal de la superficie de apoyo a la que consideramos lisa, que son fuerzas verticales), luego aplicas la Segunda Ley de Newton, y tienes la ecuación:
T = M*acp (1).
Luego, tienes los datos:
M = 12 Kg (masa del cuerpo),
R = 3 m (radio de giro, que es igual a la longitud de la cuerda),
f = 5 v/min = 5/60 = 1/12 v/s (frecuencia de giro).
Luego, planteas la expresión de la velocidad angular en función del radio de giro y de la frecuencia, y queda:
ω = 2π*f = 2π*(1/12) = π/6 rad/s.
Luego, planteas la expresión del módulo de la aceleración centrípeta en función del radio de giro y de la velocidad angular, y queda:
acp = ω2*R = (π/6)2*3 = π2/12 rad/s2 ≅ 0,822 rad/s2.
Luego, reemplazas valores en la ecuación señalada (1), y queda:
T = 12*π2/12 = π2 N ≅ 9,870 N.
Luego, planteas la expresión de la velocidad tangencial en función del radio de giro y de la velocidad angular, y queda:
v = R*ω = 3*(π/6) = π/2 rad/s ≅ 1,571 m/s.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/1/197)
Observa que tienes el gráfico tiempo-posición, y que el mismo es la unión de dos segmentos, lo que corresponde a dos etapas de Movimiento Rectilíneo Uniforme, y por lo que tienes que la expresión de la función constará de dos trozos:
a)
Observa que el primer segmento une los puntos (0,0) y (40,450), y que su pendiente queda expresada:
m1 = (450-0)/(40-0) = 450/40 = 45/4,
por lo que tienes que la velocidad del móvil en este primer tramo es:
v1 = 45/4 m/s = 11,25 m/s.
b)
Observa que el segundo segmento une los puntos (40,450) y (60,0), y que su pendiente queda expresada:
m2 = (0-450)/(60-40) = -450/20 = -45/2 m/s = -22,5 m/s,
por lo que tienes que la velocidad del móvil en este primer tramo es:
v2 = -45/2 m/s - 22,5 m/s.
c)
Planteas las expresiones de los desplazamientos (Δx = xf - xi) correspondientes a los tramos, y queda:
Δx1 = 450 - 0 = 450 m,
luego planteas la expresión de la distancia recorrida en este tramo (D = |Δx|), y queda:
D1 = |Δx1| = |450| = 450 m;
Δx2 = 0 - 450 = -450 m,
luego planteas la expresión de la distancia recorrida en este tramo (D = |Δx|), y queda:
D2 = |Δx2| =|-450| = 450 m,
luego planteas la expresión de la distancia total recorrida, y queda:
D = D1 + D2 = 450 + 450 = 900 m.
d)
Planteas la expresión del desplazamiento total, y queda:
Δx = Δx1 + Δx2 = 450 + (-450) = 450 - 450 = 0,
por lo que tienes que la posición inicial de todo el recorrido (observa en tu gráfico, y es: xi = 0, en el instante: ti = 0), y que la posición final de todo el recorrido (observa en tu gráfico, y es: xf = 0, en el instante: ti = 60 s), por lo que tienes que la posición inicial y la posición final son ambas: x = 0.
e)
Observa que en el primer tramo tienes que el móvil se aleja de la posición inicial y que en el segundo tramo se acerca a ella, y que el intervalo de tiempo correspondiente al segundo tramos es:
Δt2 = 60 - 40 = 20 s.
f)
En el primer tramo de su recorrido tienes que el móvil se desplaza con Movimiento Rectilíneo Uniforme cuya velocidad es: v1 = 11,25 m/s, entre los instantes: ti = 0 y tf = 40 s, desde la posición inicial: xi = 0 y la posición final: xf = 450 m;
y en el segundo tramo de su recorrido tienes que el móvil se desplaza con Movimiento Rectilíneo Uniforme cuya velocidad es: v2 = -22,5 m/s, entre los instantes: ti = 40 s y tf = 60 s, desde la posición inicial: xi = 450 m y la posición final: xf = 0.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 15/1/198)
Consideramos que el cuerpo se desplaza sobre una superficie horizontal, y que el sentido de su desplazamiento es hacia la derecha.
a)
Observa que sobre el cuerpo actúan cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos (observa que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s2):
Peso: P = M*g = 8*10 = 80 N, vertical, hacia abajo;
Acción normal de la superficie: N, vertical, hacia arriba;
Fuerza aplicada sobre el cuerpo: F = 28 N, horizontal, hacia la derecha;
Rozamiento de la superficie: fr = 4 N, horizontal, hacia la izquierda;
y, luego, solo queda que hagas el diagrama de fuerzas correspondiente.
b)
Aplicas la Segunda Ley de Newton (recuerda que la dirección del desplazamiento del cuerpo es horizontal), y queda el sistema de ecuaciones:
F - fr = M*a,
N - P = 0;
luego, reemplazas valores, y queda:
28 - 4 = 8*a, de aquí despejas: a = 24/8 = 3 m/s2;
N - 80 = 0, de aquí despejas: N = 80 N.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 15/1/19Javi
el 15/1/19Buenas...
Para ayudarte a entender la gráfica, tienes que fijarte en las unidades en la que se representan, en este caso, espacio (en metros), frente a tiempo(en segundos), por lo que si recuerdas la formula de la velocidad en un tramo a velocidad constante, veríamos que es: V=e/t.e
Entendemos por el primer tramo, como la recta ascendente,(que al ser recta entendemos que es un movimiento uniforme a velocidad constante, y en el eje de las y, está representada la distancia recorrida(espacio): X).
Por lo tanto para el apartado a) bastaría con que te fijes en las cordenadas del puntofinal de ese tramo, para ver el espacio recorrido y en cuanto tiempo, y de ese modo puedes encontrar la velocidad.
En en apartado b) ten en cuenta, en lugar de las coordenadas del punto la distancia en la que se encontraba el coche teledirigido, es decir, los metros recorridos(espacio representado en el eje y) que te indica como X. Dicho de otra forma, supón que el coche regresa. y el tiempo, en ese caso, será el tiempo total menos el tiempo que ha empleado en realizar el primer tramo. y aplicando la formula anterior...
Espero haberte ayudado, intenta los demás puntos, e imaginar el movimiento descrito por el coche, teniendo en cuenta los datos de la gráfica.
Un saludo.
-
Hola, ¿Alguien me ayudar con el apartado f?
Resultados hasta ahora
a. Muelle B : 16,66mm
Muelle C: 25mm
Muelle D : 50mm
b.2 muelles
c.33,33mm
d. 17,32 rad/s
e. 0,01 cos(17,32t)
-1,73 sen(17,32t)
Fernando Alfaro
el 15/1/19Apartado f.
Se pide hallar x y v para: Epk = Ec => ½ kx2 = ½mv2 (1) Sea Et la energía total.
Se puede expresar la energía cinética en x como:
½mv2 = Et - Epk = ½kA2 - ½kx2
Sustituyendo en (1):
½ kx2 = ½kA2 - ½kx2 => kx2 = ½kA2 => x2 = ½A2 => x = ±√(½A2 ) => x = ± √½ A => x = ±√(2)/2 A
De forma similar, se puede expresar:
½kx2 = ½mvm2 - ½mv2 donde vm es la velocidad máxima.
Sustituyendo en (1):
½mvm2 - ½mv2 = ½mv2 => mv2 = ½mvm2 => v2 = ½ vm2 => v = ±√(½vm2) => v = ± √(2)/2 vm
Si A = 0.01m y vm = 1.73 m/sEntonces x ≅ ± 0.0707 m y v ≅ ± 1.22 m/s
Espero haberte ayudado en algo.
































