-
En el tema de ondas , que significa que el periodo de obtenga con la ecuación v / lambda????
Antonio Silvio Palmitano
el 6/1/19Podrías abordar el problema en esta forma.
Observa que un punto específico de la onda se desplaza una longitud de onda cuando ha transcurrido un periodo completo de oscilación, por lo que tienes que la expresión del módulo de la velocidad de propagación es:
v = λ/T,
luego, multiplicas por T y divides por v en ambos miembros, y la expresión para el periodo queda:
T = λ/v;
luego, si expresas al periodo en función de la frecuencia de oscilación, la ecuación remarcada queda:
1/f = λ/v,
inviertes las expresiones en ambos miembros, y queda:
f = v/λ.
Espero haberte ayudado.
-
BUENAS NOCHES UNICOOS, ME PODEIS AYUDAR CON ESTE PROBLEMA?? LO HE RESUELTO Y ME DE LA Vo=33'3m/s, e=150m, la a=-3'7m/s2 y el tiempo=9s. A LA HORA DE CALCULAR EL COEFICIENTE DE ROZAMIENTO, TENGO PROBLEMAS. ME PODEIS AYUDAR?? MUCHAS GRACIAS
Un coche circula a 120km/h y empieza a frenar hasta que se detiene despues de 150m. Calcular el coeficiente de rozamiento
Antonio Silvio Palmitano
el 6/1/19Considera un sistema de referencia con eje OX horizontal, con sentido positivo acorde al desplazamiento del coche, con origen de coordenadas en el punto donde el conductor aplica los frenos, con instante inicial: ti = 0 en el momento en que comienza a frenarse el coche.
Luego, tienes los datos:
vi = 120 Km/h = 120*1000/3600 = 100/3 m/s (rapidez inicial del coche),
vf = 0 (rapidez final del coche, que alcanza el reposo),
Δx = 150 m (desplazamiento del coche);
luego, planteas la ecuación velocidad-desplazamiento de Movimiento Rectilíneo Uniformemente Variado, y queda:
2*a*Δx = vf2 - vi2, de aquí despejas:
a = (vf2 - vi2) / (2*Δx), reemplazas valores, y queda:
a = (0 - 100/3) / (2*150) = (-100/3) / 300 = -1/9 m/s2 (1).
Luego, planteas la expresión del módulo de la fuerza de rozamiento (sería conveniente que dibujes un diagrama de fuerzas), y queda:
fr = μ*M*g.
Luego, aplicas la Segunda Ley de Newton (observa el sentido de la fuerza de rozamiento), y queda:
-μ*M*g = M*a, divides por -M*g en ambos miembros, y queda:
μ = -a/g, reemplazas el valor señalado (1) y el valor del módulo de la aceleración gravitatoria terrestre, y queda:
μ = -(-1/9) / 9,8 = 1/88,2 ≅ 0,011.
Espero haberte ayudado.
-
Jerónimo
el 6/1/19Si llamamos E1 al campo creado por la carga que está en (0,5) y E2 al campo creado por la carga que está en (0,-5). Como las cargas son iguales , el E será nulo en la recta que une ambas cargas y donde se cumpla que E1=E2 (considero sólo módulos porque ambos vectores están sobre el eje OY.
E1=E2 Llamamos x a la distancia de la carga de arriba hasta donde se anulan los campos kq/x²=Kq/(10-x)² x=5m , por lo que el punto donde E es nulo será (0,0)
Respecto a la 2º pregunta , como el campo eléctrico es un campo de fuerzas centrales, el potencial eléctrico sólo depende de la distancia al centro (fuente de campo), observa que el punto (1,0) y el (-1,0) están a la misma distancia relativa respecto de las dos cargas creadoras de campo, V en (1,0) es igual a V en (-1,0) y el trabajo=qΔV será cero
Antonio Silvio Palmitano
el 6/1/19Observa que los campos son colineales solamente en los puntos del eje OX, con excepción de los puntos donde están ubicadas las cargas.
Luego, observa que tienes dos cargas positivas, por lo que tienes tres casos:
1)
los dos campos tienen sentido negativo para los puntos del eje OX que se encuentran a la izquierda del punto (-5,0),
2)
los dos campos tienen sentido positivo para los puntos del eje OX que se encuentran a la derecha del punto (5,0),
3)
los dos campos tienen sentidos opuestos para los puntos del eje OX que están entre los puntos (-5,0) y (5,0).
a)
Como las cargas son iguales, tienes que el punto medio entre ellas, que es el origen de coordenadas, es donde tienes que el campo resultante es nulo, y su valor queda planteado (observa que llamamos q1 a la carga ubicada en el punto (-5,0) del eje OX):
E = E1 + E2 = +k*q/52 - k*q/52 = 0.
b)
Planteas el valor de la energía potencial en el punto inicial (1,0) (observa que las distancias son: d1 = 6 m y d2 = 4 m), y queda:
EPi = k*q1*q/d1 + k*q2*q/d2, extraes factores comunes, y queda:
EPi = k*q*(q1/d1 + q2/d2), reemplazas valores, y queda:
EPi = 9*109*1*(2*10-3/6 + 2*10-3/4), extraes factor común y resuelves el coeficiente, y queda:
EPi = 18*106*(1/6 + 1/4), resuelves el agrupamiento, y queda:
EPi = 18*106*5/12, resuelves, y queda:
EPi = (15/2)*106 = 7,5*106 J.
Planteas el valor de la energía potencial en el punto final (-1,0) (observa que las distancias son: d1 = 4 m y d2 = 6 m), y queda:
EPf = k*q1*q/d1 + k*q2*q/d2, extraes factores comunes, y queda:
EPf = k*q*(q1/d1 + q2/d2), reemplazas valores, y queda:
EPf = 9*109*1*(2*10-3/4 + 2*10-3/6), extraes factor común y resuelves el coeficiente, y queda:
EPf = 18*106*(1/4 + 1/6), resuelves el agrupamiento, y queda:
EPf = 18*106*5/12, resuelves, y queda:
EPf = (15/2)*106 = 7,5*106 J.
Luego, planteas la expresión de la variación de energía potencial, y queda:
ΔEP = EPf - EPi = 7,5*106 - 7,5*106 = 0;
luego, planteas la ecuación trabajo-energía, y el trabajo neto que es necesario aplicar para trasladar la carga unitaria entre los puntos indicados, queda:
W = ΔEP = 0.
Observa que este resultado muestra que en una parte del trayecto se debe realizar trabajo para equilibrar a la fuerza electrostática resultante, mientras que en la otra parte es el campo resultante el que realiza trabajo (o sea, en palabras sencillas, en una parte empujas y en la otra te dejas llevar), y que ambos trabajos se compensan.
Espero haberte ayudado.
-
BUENAS UNICOOS! ME PODEIS AYUDAR CON ESTE PROBLEMA?
Calcular la aceleracion y la velocidad con la que un cuerpo llega al final de un plano inclinado de 60º si mide 35m y el coeficiente de rozamiento es 0'3.
SE QUE EL Ef= 35m, Vo=0m/s Y HE CALCULADO EL SUMATORIO DE FUERZAS Y ME DA 7'02N PERO AUN ASI EN LA FORMULA DE F=M*A ME FALTA LA MASA Y LA ACELERACION.
Antonio Silvio Palmitano
el 6/1/19Establece un sistema de referencia con eje de posiciones (alturas) OY vertical, con sentido positivo hacia arriba, y con origen de coordenadas al nivel del punto más alto del plano inclinado (observa que consideramos que el cuerpo parte desde el reposo, y desde el punto más alto del plano inclinado).
Luego, planteas las expresiones de la energía potencial y de la energía cinética iniciales, y queda:
EPi = M*g*hi = M*g*L*senθ,
ECi = 0;
y la expresión de la energía mecánica inicial queda:
EMi = EPi + ECi = M*g*L*senθ + 0 = M*g*L*senθ (1).
Luego, planteas las expresiones de la energía potencial y de la energía cinética finales, y queda:
EPf = M*g*hf = M*g*0 = 0,
ECi = (1/2)*M*vf2;
y la expresión de la energía mecánica inicial queda:
EMf = EPf + ECf = 0 + (1/2)*M*vf2 = (1/2)*M*vf2 (2).
Luego, planteas la expresión del trabajo de la fuerza de rozamiento (sería muy conveniente que dibujes un diagrama de fuerzas usual para planos inclinados), y queda:
Wfr = -fr*L = -μ*M*g*cosθ*L = -μ*M*g*L*cosθ (3).
Luego, planteas la ecuación energía-trabajo, y queda:
EMf - EMi = Wfr,
sustituyes las expresiones señaladas (2) (1) (3), y queda:
(1/2)*M*vf2 - M*g*L*senθ = -μ*M*g*L*cosθ,
multiplicas por 2 y divides por M en todos los términos de la ecuación, y queda:
vf2 - 2*g*L*senθ = -2*μ*g*L*cosθ,
sumas 2*g*L*senθ en ambos miembros, y queda:
vf2 = 2*g*L*senθ - 2*μ*g*L*cosθ,
extraes factores comunes en el segundo miembro, y queda:
vf2 = 2*g*L*(senθ - μ*cosθ),
extraes raíz cuadrada positiva en ambos miembros, y queda:
vf = √( 2*g*L*(senθ - μ*cosθ) ),
que es la expresión del módulo de la velocidad con la que el cuerpo llega al pie del plano.
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
cerin laissaoui
el 6/1/19Buenas Antonio y gracias por tu respuesta. Mi pregunta es si no hay otra manera de resolver el ejercicio porque nunca nos habia hecho falta la formula de la energia potencial/cinetica. No se puede resolver mediante sumatorio de fuerzas? Muchas gracias y espero tu respuesta
Fernando Alfaro
el 6/1/19Se puede si, muy similar al planteo del ejercicio anterior pero en plano inclinado.
Plantea un sistema de coordenadas con el eje x paralelo al plano inclinado, y el eje y perpendicular.
Descompones el peso en sus componentes Px y PyPx = P sin(θ) y Py = Pcos(θ)
N = Py = Pcos(θ)
Fr = μN = μPcos(θ)
∑Fy = N - Py = 0
∑Fx = Px - Fr = P sin(θ) - μPcos(θ) = P(sin(θ) - μcos(θ)) = mg (sin(θ) - μcos(θ)) = ma => a = g (sin(θ) - μcos(θ))
vf2 - vi2 = 2aΔx = 2*Δx*g*(sin(θ) - μ*cos(θ)) y como vi = 0vf = √(2*Δx*g*(sin(θ) - μ*cos(θ))) que es la misma formula a la que ha llegado el colega Antonio.
Reemplazando valores:
vf = √(2*35*9.8*(sin(60) - 0.3*cos(60))) = 22.16 m/s
a = 9.8*(sin(60) - 0.3*cos(60))) = 7.02 m/s2
Ten en cuenta que la formula: vf2 - vi2 = 2aΔx solo aplica para aceleraciones constantes. (MRUV) -
¡Hola! En el tema de ondas de 2º bach, en la formula general de la onda,(y=A*sen(wt-kx)) , qué significa que a veces haya un Pi multiplicando el seno? También por qué a veces la fórmula es con coseno?
Fernando Alfaro
el 6/1/19Pi multiplicando el seno? dentro o fuera del paréntesis de la función seno?
Dentro del paréntesis puede ser por:
Sustituir: w = 2πf y k = 2π/λ y extraer factor común 2π. Pero ese 2π queda dentro de la función seno.
También puede aparecer π dentro del paréntesis por conversión de grados a radianes. α° = α° π rad/180°
Un termino π multiplicando al seno fuera del paréntesis se me ocurre por derivación, pero eso ya no es la función y(x, t). Derivando respecto a t daría como resultado la ecuación de la velocidad: v(x, t).
Te recomiendo el vídeo Onda transversal en una cuerda 02
Respecto a la segunda pregunta.
En la formula general de la onda está faltando el termino de la fase φ0
La ecuación general con fase es: y(x, t) = Asen(wt - kx + φ0) (Simplificando wt - kx = α)
sen(α + π/2) = cos(α) de modo que si φ0 = π/2 rad (o 90°) se puede sustituir la función sen por coseno con fase cero.
En términos mas generales: sen(α + φ0 + π/2) = cos(α + φ0) por lo que se puede sustituir entre función seno y coseno según el valor del termino de la fase.
sen(α + φa ) = cos(α + φb ) con φa = φb + π/2
-
BUENAS UNICOOS!! ME PODEIS AYUDAR CON ESTE PROBLEMA? SE QUE LOS 90KM/H=25M/S, LA Vf=0, Eo= 0, Y HE CALCULADO LA ACELERACION Y ME DA -1'96M/S2 (SIGUIENDO UNOS VIDEOS DEL PROFE) Y EL ESPACIO RECORRIDO ME DA 159'44M PERO NO CONSIGO TERMINAR DE RESOLVER EL PROBLEMA PORQUE NO ESTOY SEGURA DE LOS RESULTADOS. ME PODEIS AYUDAR PORFAVOR??
Un coche circula a 25km/h por un suelo horizontal i empieza a frenar. Calcular la distancia recorrida hasta que se detiene si el coeficiente de rozamiento es 0'2.
Antonio Silvio Palmitano
el 6/1/19Observa que sobe el coche actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos (consideramos que el coche se desplaza hacia la derecha):
Peso: P = M*g, vertical hacia abajo,
Acción normal del suelo: N, vertical hacia arriba,
Rozamiento del suelo: fr = μ*N, horizontal hacia la izquierda;
luego, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
-fr = M*a, de aquí despejas: a = -fr/M = -μ*N/M (1),
N - P = 0, de aquí despejas: N = P = M*g (2);
luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), simplificas, y queda:
a = -μ*g,
que es la expresión de la aceleración del coche.
Luego, tienes la velocidad inicial:
vi = 25 Km/h = 25*1000/3600 = 125/18 m/s,
y tienes la velocidad final:
vf = 0;
luego, planteas la ecuación desplazamiento-velocidad de Movimiento Rectilíneo Uniformemente Acelerado, y queda:
2*a*Δx = vf2 - vi2,
sustituyes la expresión remarcada de la aceleración en el primer miembro, resuelves el signo, y queda:
-2*μ*g*Δx = vf2 - vi2,
multiplicas por -1, y divides por 2*μ*g en ambos miembros, y queda:
Δx = -(vf2 - vi2) / (2*μ*g),
cancelas el término nulo (recuerda: vf = 0), y queda:
Δx = -vi2 / (2*μ*g),
y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
Francisco Javier Tinoco Tey
el 6/1/19Fernando Alfaro
el 6/1/19cerin laissaoui
el 6/1/19Francisco Javier Tinoco Tey
el 6/1/19Antonio Silvio Palmitano
el 6/1/19La observación de Francisco es correcta, en este ejercicio se me escapó un signo negativo al consignar la expresión del desplazamiento, que en este ejercicio lleva signo positivo.
Aunque, aclaremos que en general, el signo del desplazamiento depende de las coordenadas de los puntos final e inicial, y su expresión es:
Δx = xf - xi,
y su signo depende de los valores de las coordenadas.
Espero haberte ayudado.
-
Buenas tardes. Os dejo el enunciado de mi problema relacionado con el tema de torques junto a la resolución que he planteado. Mi única duda es la indicada en azul. Cuando aplico sumatorio de torques igual a momento de inercia por aceleración angular, los datos de cual de las dos poleas son las que tengo que introducir? Yo he introducido los de la polea mas grande, no se si tendría que introducir los de la polea pequeña o incluso sumar los dos momentos de inercia como se hace en otros ejercicios. Digo polea grande/pequeña aunque entiendo que se trata de la misma polea solo que el torque se aplica en el radio pequeño..
Muchas gracias a todo el equipo de Unicoos!
-
Hola, alguien me ayúda con estos ejercicios por favor? Y a que tema pertenecen ya
 que no tengo idea, gracias.
que no tengo idea, gracias.Antonio Silvio Palmitano
el 6/1/198)
Debes comenzar por expresar los volúmenes con la misma unidad de medida:
V1 = 1 cm3 (aquí caben: N1 = 3 gotas),
V2 = 6 m3 = 6 * 1 m3 = 6 * (100 cm)3 = 6*1000000 cm3 = 6000000 cm3 = 6*106 cm3 (aquí caben: N2 gotas).
Luego, planteas la ecuación de proporciones entre las cantidades de gotas y los volúmenes:
N2/V2 = N1/V1, reemplazas valores, y queda:
N2/6*106 = 3/1, multiplicas por 6*106 en ambos miembros, y queda:
N2 = (3/1)*6*106 = 18*106 gotas.
9)
Tienes los datos:
p = a determinar (presión),
F = 25 GN = 25*109 N (fuerza aplicada),
A = 5 Mm2 = 5*106 m2 (área de la superficie de aplicación);
luego, planteas la expresión de la presión, y queda:
p = F/A, reemplazas datos, resuelves, y queda:
p = 25*109 / 5*106 = (25/5)*(109/106) = 5*103 Pa = 5 KPa.
10)
Tienes la expresión de la fuerza aplicada:
F = 6 GN = 6*109 N.
Tienes la expresión del desplazamiento:
Δs = 12 am = 12*10-18 m.
Luego, planteas la expresión del trabajo en función de la fuerza aplicada y del desplazamiento (observa que suponemos que fuerza y desplazamiento tienen direcciones iguales y sentidos iguales), y queda:
W = F*Δs, reemplazas valores, y queda:
W = 6*109 * 12*10-18 = (6*12)*(109*10-18) = 72*10-9 J,
aquí introduces el factor neutro 103*10-3 (observa que esta cantidad es igual a 1), y queda:
W = 72*(103*10-3)*10-9 = (72*103)*(10-3*10-9) = 72*103*10-12 J = 72*103 pJ.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 5/1/19Nos ubicamos en el punto más bajo del valle semicircular.
Observa que sobre el camión actúan tres fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: PC = M*g, hacia abajo,
Acción normal del la superficie semicircular: NS, hacia arriba,
Acción normal del bloque: NB, hacia abajo;
luego, considera un sistema de referencia con eje OY vertical con sentido positivo hacia arriba (hacia el centro de la semicircunferencia), aplicas la Segunda Ley de Newton, y tienes la ecuación:
NS - NB - PC = M*acp,
sustituyes las expresiones del peso del camión y de la aceleración centrípeta, y queda:
NS - NB - M*g = M*v2/R (1).
Observa que sobre el bloque actúan dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: PB = m*g, hacia abajo,
Reacción normal del camión: NB, hacia arriba;
luego, considera un sistema de referencia con eje OY vertical con sentido positivo hacia arriba (hacia el centro de la semicircunferencia), aplicas la Segunda Ley de Newton, y tienes la ecuación:
NB - m*g = m*acp,
sustituyes las expresiones del peso del camión y de la aceleración centrípeta, y queda:
NB - m*g = m*v2/R (2).
Luego, tienes los datos:
NB = 1,04*m*g,
R = 600 m;
luego, reemplazas estos datos en las ecuaciones señaladas (1) (2), y queda el sistema de ecuaciones:
NS - 1,04*m*g - M*g = M*v2/600 (1*),
1,04*m*g - m*g = m*v2/600 (2*),
reduces términos semejantes en la ecuación señalada (2*), y queda:
0,04*m*g = m*v2/600,
multiplicas por 600 y divides por m en ambos miembros, y queda:
24*g = v2,
extraes raíz cuadrada positiva en ambos miembros, y queda:
√(24*g) = v,
que es el módulo de la velocidad lineal del sistema camión-bloque en el punto más bajo de la superficie semicircular;
luego, puedes sustituir la expresión remarcada en la ecuación señalada (1*), para luego despejar la expresión del módulo de la acción normal que la superficie semicircular sobre el camión; y luego lo único que te queda es hacer los cálculos.
Espero haberte ayudado.
Angel
el 6/1/19Fernando Alfaro
el 6/1/19La aceleración es la aceleración centrípeta, o aceleración normal de un movimiento circular, que está dirigida hacia el centro de la circunferencia, y en el punto mas bajo alineada con el eje OY y las fuerzas mencionadas.
No es la aceleración lineal, o tangencial del movimiento. No se están suponiendo ni fuerzas ni aceleraciones tangenciales en dicho punto del movimiento circular.
Ayude a despejar la duda?
-
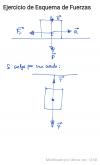
HOLAA! LA A LA FUERZA VA HACIA LA DERECHA Y LA B HACIA ARRIBA? YO LO INTERPRETO ASI, ESTA BIEN?? MUCHAS GRACIAS Y BUENAS NOCHES!!
Identifica las fuerzas que actúan sobre los cuerpos
siguientes:
a) Un coche que acelera por una carretera horizontal.
b) Un cuerpo que cuelga del techo mediante un cable.