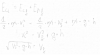-
Hola buenas, en este problema de un oscilador he obtenido la variacion de x a partir de los datos igualandola al peso, hallando así el alargamiento máximo.Para el segundo apartado he procedido a usar ese alargamiento como amplitud de mi onda,he calculado w=raiz(k/m) y he armado la ecuacion de onda como (2/3)alargamiento max = Amplitud(alargamiento max)cos(wcalculada*t+fase incial=0) y a partir de ahí he despejado el tiempo, sería correcto?
Antonio Silvio Palmitano
el 12/1/19Tienes los datos:
k = 1 N/m (constante elástica del muelle),
M = 24 g = 0,024 Kg (masa del oscilador;
de donde has planteado correctamente la expresión de la pulsación (frecuencia angular), y queda:
ω = √(k/M) = √(1/0,024) ≅ √(41,667) ≅ 6,455 rad/s.
Luego, planteas la condición de equilibrio (el oscilador cuelga en reposo), y queda:
k*Δs = M*g, de donde despejas:
Δs = M*g/k = 0,024*9,8/1 = 0,2352 m.
Luego, establece un sistema de referencia con eje de posiciones (alturas) OY con origen en el punto correspondiente al oscilador colgado y en reposo, con sentido positivo hacia arriba, con instante inicial: ti = 0 correspondiente al momento en que el oscilador es liberado, y las expresiones de la posición, de la velocidad y de la aceleración del oscilador quedan:
y(t) = A*cos(ω*t),
v(t) = -ω*A*sen(ω*t),
a(t) = -ω2*A*cos(ω*t);
luego, observa que tienes las condiciones iniciales:
y(0) = Δs = 0,2352 m (posición inicial, en el punto en el cuál el resorte está relajado),
v(0) = 0 (recuerda que la velocidad inicial del oscilador es nula),
a(0) = a determinar;
luego, sustituyes en las expresiones de las funciones, resuelves los argumentos de los factores trigonométricos (recuerda que el instante inicial es: ti = 0), y queda:
0,2352 = A (amplitud de oscilación),
0 = 0,
a(0) = -ω2*A = -( √(1/0,024) )2*0,2352 = -0,2352/0,024 = -9,8 m/s2 (aceleración del oscilador en el instante inicial, observa que su valor es extremo mínimo);
luego, sustituyes valores en las expresiones de las funciones, resuelves coeficientes, y queda:
y(t) = 0,2352*cos(6,455*t) (1),
v(t) = -1,5182*sen(6,455*t) (2),
a(t) = -9,8*cos(6,455*t) (3).
a)
Observa que el alargamiento corresponde al punto simétrico al punto de partida, por lo que tienes que la la expresión del estiramiento máximo del muelle es:
ΔsM = 2*A = 2*0,2352 = 0,4704 m.
b)
Planteas la condición de la posición del punto en estudio, y queda:
y(t) = (2/3)*A,
sustituyes la expresión señalada (1) en el primer miembro, y el valor de la amplitud en el segundo, y queda:
0,2352*cos(6,455*t) = (2/3)*0,2352, divides por 0,2352 en ambos miembros, y queda:
cos(6,455*t) = 2/3,
compones en ambos miembros con la función inversa del coseno (no olvides posicionar tu calculadora en radianes, y observa que elegimos el primer valor positivo), y queda:
6,455*t ≅ 0,8411, divides por 6,455 en ambos miembros, y queda:
t ≅ 0,1303 s;
luego, observa que si reemplazas este valor remarcado en las expresiones señaladas (2) (3) también puedes obtener los valores de la velocidad y de la aceleración del oscilador en el punto en estudio.
Espero haberte ayudado.
-
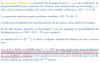
Buenos dias , necesitaría ayuda con el siguiente problema ya que me lío un poco con las fórmulas:
Plano inclinado 40 grados sobre la horizontal, con una longitud de 1metro.
Un bloque de 5kg se sitúa en la parte superior del plano y se deja caer. Coeficiente de rozamiento 0’5: Dibuja las fuerzas que actúan sobre el objeto y la aceleración de bajada, tiempo que tarda en llegar al final del plano y la velocidad de llegada.
Antonio Silvio Palmitano
el 12/1/19Observa que sobre el bloque actúan tres fuerzas, de las que indicamos sus módulos direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo;
Acción normal del plano inclinado: N, perpendicular al plano, hacia arriba;
Rozamiento del plano inclinado: fr = μ*N, paralela al plano inclinado, hacia arriba;
y solo queda que dibujes el diagrama de fueras correspondiente.
Luego, considera un sistema de referencia con origen en el punto más alto del plano inclinado, con eje OX paralelo a dicho plano con sentido positivo hacia abajo, y con eje OY perpendicular a dicho plano con sentido positivo hacia arriba.
Luego, aplicas la Segunda Ley de Newton y tienes el sistema de ecuaciones (observa que debes descomponer el peso del bloque según las direcciones de los ejes coordenados):
P*senθ - fr = M*a,
N - P*cosθ = 0;
luego, sustituyes las expresiones de los módulos del peso y del rozamiento, y queda:
M*g*senθ - μ*N = M*a,
N - M*g*cosθ = 0, de aquí despejas:
N = M*g*cosθ (1);
luego, sustituyes la expresión señalada (1) en la primera ecuación, y queda:
M*g*senθ - μ*M*g*cosθ = M*a, divides por M en todos los términos de esta ecuación, y queda:
g*senθ - μ*g*cosθ = a, extraes factor común, y queda:
(senθ - μ*cosθ)*g = a (2).
Luego, reemplazas datos que tienes en tu enunciado en las expresiones señaladas (1) (2), y queda:
N = 5*9,8*cos(40°) ≅ 5*9,8*0,7660 ≅ 37,5362 N,
a = ( sen(40°) - 0,5*cos(40°) )*9,8 ≅ (0,6428 - 0,5*0,7660)*9,8 ≅ 0,2598*9,8 ≅ 2,5457 m/s2.
Luego, planteas las expresiones de la función posición y de la función velocidad de Movimiento Rectilíneo Uniformemente Variado (observa que el bloque se desplaza con dirección y sentido positivo del eje OX, y que consideramos el instante inicial: ti = 0 correspondiente al inicio del desplazamiento del bloque), y queda:
x = xi + vi*t + (1/2)*a*t2,
v = vi + a*t;
luego, reemplazas valores iniciales (xi = 0 y vi = 0), cancelas términos nulos, reemplazas el valor de la aceleración, resuelves coeficientes, y queda:
x ≅ 1,2729*t2,
v = 2,5457*t;
luego, reemplazas los datos finales (que corresponden a la llegada del bloque al pie del plano inclinado):
tf = a determinar, xf = 1 m, vf = a determinar, y queda:
1 ≅ 1,2729*tf2,
vf = 2,5457*tf;
de la primera ecuación despejas:
tf≅ √(1/1,2729) ≅ √(1,1282) ≅ 1,0622 s;
luego, reemplazas este último valor remarcado en la segunda ecuación, y queda:
vf ≅ 2,5457*1,0622 ≅ 2,7040 m/s.
Espero haberte ayudado.
-
*Buenas tardes, quisiera saber si es posible imantar la sal (cloruro sodico), dentro del agua. Si es afirmativo , como seria el procedimiento?
*Es posible hacer un motor solamente con imanes
Gracias
Raúl RC
el 12/1/19Fernando Alfaro
el 13/1/19Dudo mucho que se pueda imantar permanentemente cualquier sustancia en estado liquido o gaseoso. Quizás en el foro de química te puedan dar una respuesta mas firme en este sentido.
Según la teoría del magnetismo de Ampere, el magnetismo por si mismo no existiría, sería producto de campos magnéticos generados por corrientes eléctricas internas en la sustancia. Cuando estas corrientes internas están ordenadas de forma tal que sus campos magnéticos no se cancelan y por el contrario, se refuerzan, el resultado sería un imán.
No veo porque no se se pueda inducir este tipo de movimiento ordenado en los iones de NaCl disueltos en agua. Simplemente con un bobinado y una corriente continua pulsaste. Lo que dudo es que este movimiento de cargas se mantenga, y de forma ordenada durante mas de algunas fracciones de segundo sin la corriente inductora dentro de una estructura liquida.
Mas a fondo:
Según mi física general (que es un poco viejo), todas las sustancias tienen propiedades magnéticas y se pueden clasificar según su permeabilidad relativa Km , respecto al vació, siendo la permeabilidad magnética del vació igual a 1.
Si Km < 1 => Clasifica como diamagnética.
Si Km > 1 => Clasifica como paramagnética.
Si Km >> 1 => Clasifica como ferromagnética. (Nótese que esta distinción entre sustancia paramagnética y ferromagnética es algo subjetiva).
La Temperatura de Curie, en principio estaría definida para sustancias ferromagnéticas. La permeabilidad magnética de una sustancia ferromagnética desciende con el aumento de la temperatura, y la temperatura a la cual su permeabilidad magnética desciende aproximadamente a la unidad se llama Temperatura de Curie.
Si quieres puedes tomarte el tiempo de hacer una investigación mas extensa, pero he hecho una rápida comparación de algunas sustancias ferromagnéticas conocidas y la temperatura de Curie siempre es menor que el punto de fusión. Dando cierto soporte experimental a mi supuesto de que en principio, los líquidos no pueden ser magnetizados permanentemente.
Si se revierte el razonamiento y se enfría lo suficiente una sustancia cualquiera, esta comienza a presentar propiedades ferromagnéticas? Realmente no lo se.
Si haces las pruebas de laboratorio, luego nos cuentas ;)
Respecto a la segunda pregunta. Solamente con imanes no lo se. Pero en teoría es posible si, siempre y cuando los imanes, o algunos de ellos pierdan magnetismo. Luego habría que re-imantarlos, es decir, estarían jugando el papel de "batería"
Un imán permanente es comparable con un inductor "cargado" y este tiene asociada una energía acumulada que de algún modo podría ser utilizada como energía mecánica.
-
Fernando Alfaro
el 10/1/19Densidad del corcho: dc = 0.72 g/cm3 = 720 Kg/m3
Densidad del liquido: dL = 1.2 g/cm3 = 1200 Kg/m3
Volumen del corcho: Vc = πr2 h = π * 0.022 * 0.05 = 2π *10-5 m3
Masa del corcho: mc = dc Vc = 720 * 2π * 10-5 = 0.0144π Kg
Peso del corcho: Pc = mc g = 0.0144π * 9.8 = 0.141π N vertical hacia abajo (sentido negativo)
La fuerza de empuje es igual al peso del volumen del liquido desalojado:
Fuerza de empuje: Fe = dL Vc g = 1200 * 2π *10-5 * 9.8 = 0.235π N vertical hacia arriba (sentido positivo)
∑Fy = Fe - P = 0.235π - 0.141π = 0.0941π N => fuerza neta positiva => sentido hacia arriba => acelerara hacia la superficie.
∑Fy = may => ay = ∑Fy /m => ay = 0.0941π / 0.0144π = 6.53 m/s2En la superficie Fe = P. Sea Vs el volumen del corcho sumergido.
Fe = P => dL Vs * g = mc* g => dL Vs = mc => Vs = mc / dL = 0.0144π / 1200 = 1.2π *10-5 m3
Porcentaje de corcho sumergido: %s = Vs / Vc * 100 = 1.2π *10-5 / 2π*10-5 * 100 = 60%
Porcentaje de corcho no sumergido: %ns = 100 - %s = 40%
Jerónimo
el 10/1/19r=0,02m Vcuerpo = πr²h = π0,02²0,05= 6,28.10-5 m³
h=0,05m Peso=mg=Vc dc g= 6,28.10-5 x720x9,8=0,44 N mc=6,28.10-5 x720=0,045kg
dl=1200kg/m3 Empuje=Vs dl g=6,28.10-5x1200x9,8=0,74 N Volumen del cuerpo= volumen sumergido
dc=720kg/m3 Empuje mayor que peso, el cuerpo asciende E-P=ma 0,74-0,44=0,045a a=6,6m/s²
Flotará cuando P=E Vcdcg=Vsdlg Vcx720=Vsx1200 Vs=720Vc/1200=0,6Vc 60% sumergido 40% fuera del agua
Principio de Arquímedes 01 -
Antonio Silvio Palmitano
el 10/1/19Puedes plantear las expresiones cartesianas de los vectores:
r = < 10*cos(25°) , 10*sen(25°) >,
t = < 6*cos(140°) , 6*sen(140°) >,
z = < 9*cos(340°) , 9*sen(340°) >;
luego, planteas la operación que tienes en tu enunciado, y queda:
r + t - z =
reemplazas expresiones, y queda:
= < 10*cos(25°) , 10*sen(25°) > + < 6*cos(140°) , 6*sen(140°) > - < 9*cos(340°) , 9*sen(340°) > =
sumas y restas componente a componente:
= < 10*cos(25°) + 6*cos(140°) - 9*cos(340°) , 10*sen(25°) + 6*sen(140°) - 9*sen(340°) >,
y solo queda que hagas el cálculo, y luego la representación gráfica.
Espero haberte ayudado.
-
Jerónimo
el 10/1/19Al someter al protón a una diferencia de potencial, lo aceleramos de forma que si parte del reposo, al llegar al punto B ha adquirido una velocidad
que viene determinada a partir de W=QΔV=1/2mv².
Al entrarla carga en el campo magnético aparece una fuerza magnética dirigida (según los sentidos de la velocidad y del campo magnético B) hacia arriba que hace que la carga describe una semicircunferencia de radio R hasta que choca con la pantalla
F=q(vxB)=qvBsen90º=qVB Fmagnética=Fcentríf
qvB=mv²/R v=qRB/m r=mv/qB y la distancia =2R
Campo eléctrico y magnético -
alguien sabe donde puedo mirarme problemas teoricos de fisica Campo Magnetico de 2 Bach?
Francisco Javier Tinoco Tey
el 9/1/19Espero que te sirva, un saludo ;)
-
Fernando Alfaro
el 9/1/19Movimiento de proyectil: MRU en el eje x, MRUV en el eje y
vx = vi cos(α) constante, vxh = vx , vyi = vi sen(α)
vyh2 - vyi2 = 2gh (ten en cuenta que si h tiene sentido positivo hacia arriba, g es negativo, y a fin de cuentas 2gh es negativo para h positivo)vyh2 = 2gh + vyi2 = 2gh + (vi sen(α))2 = 2gh + vi2 sen(α)2 => vyh = √(2gh + vi2 sen(α)2 ) Esta sería la componente vertical de la velocidad con la que la bola atraviesa la linea horizontal h.
El modulo de la velocidad en h es: vh = √(vxh2 + vyh2 )
vh = √ ((vicos(α))2 + 2gh + (vi sen(α))2 ) = √( vi2cos(α)2 + 2gh + vi 2sen(α)2 ) = √ (vi2(cos(α)2 + sen(α)2) + 2gh) => vh = √(vi2 + 2gh)
Conclusión, el modulo de la velocidad con la que atraviesa la linea h no depende del angulo. (Suponiendo que las bolas cruzan la linea h para empezar, que eso si depende del angulo).
También se puede deducir por energía mecánica.
Ech = Eci + Epg (de nuevo ten en cuanta que si h tiene sentido positivo hacia arriba, g tiene sentido negativo, y Epg es a fin de cuentas negativo para h positivo)
½mvh2 = ½mvi2 + mgh
vh2 = vi2 + 2gh => vh = √(vi2 + 2gh)
Alex Maestre
el 9/1/19Fernando Alfaro
el 10/1/19Al multiplicar todo por 2 para eliminar los ½ te ha faltado multiplicar también el termino gh.
La formula sería vf = √(vi2 - 2gh)
La diferencia está en el signo, que te prometo que depende de si h está por encima o por debajo de la linea de lanzamiento, y como se consideran los signos de g y h.
La explicación quedo en debe. Para mañana quizás.
Fernando Alfaro
el 10/1/19Honestamente, la formula Ech = Eci + Epg me la saqué de abajo de la manga. Fue pura conjetura.
Aquí voy con el tema de los signos y el planteo de manera mas formal.
Emi = Emf => Eci + Epi = Ecf + Epf => Ecf = Eci + Epi - Epf => Ecf = Eci - ΔEpg
El trabajo realizado por la fuerza peso (suponemos P constante) en un desplazamiento vertical es: WP = |P||Δy|cos(θ) donde θ es el angulo entre los vectores P y Δy.
Como estos vectores están alineados, cos(θ) asume solamente los valores +1 o -1, dependiendo de si los sentidos de g y Δy son iguales u opuestos.
Una breve forma de definir ΔEpg es como el trabajo realizado en contra de la fuerza peso, o el opuesto al trabajo realizado por la fuerza peso. Es decir: ΔEpg = - WP
Sustituyendo en Ecf = Eci - ΔEpg :
½mvf2 = ½mvi2 - (-Wp) = ½mvi2 + Wp = ½mvi2 + |mg||Δy|cos(θ) => ½mvf2 = ½mvi2 + m|g||Δy|cos(θ)
(Y esa es básicamente la conjetura. Mas prolijo hubiera sido: Ech = Eci + Wp . Discúlpame el mal llamado "Epg". La formula se puede deducir directamente a partir de ΔEc = Wp)
Multiplicando por 2 y dividiendo por m: vf2 = vi2 + 2|g||Δy|cos(θ) => vf = √(vi2 + 2|g||Δy|cos(θ) )
El signo del termino 2|g||Δy|cos(θ) dependerá del valor de cos(θ).
cos(θ) = 1 si g y Δy tiene el mismo sentido, y cos(θ) = -1 si g y Δy tienen sentidos opuestos.
Teniendo esto en cuenta se puede escribir (de manera algo informal):
vf2 = vi2 ± 2|g||Δy| => vf = √( vi2 ± 2|g||Δy|) y utilizando el signo correspondiente según el criterio mencionado.
Para Δy con sentido positivo y g con sentido negativo, el signo es "-", y el resultado es la formula a la que has llegado. Pero debes considerar el modulo de g.
Por ultimo, dado que g y Δy están alineados (cos(θ) = ±1), y sus sentidos están determinados por su signo, se puede establecer la relación: |g||Δy|cos(θ) = gΔy
Y por tanto: vf = √( vi2 + 2gΔy) en donde en esta última formula g y Δy se consideran valores con signo.
Espero haber aclarado la duda.
-
Hola unicoos,me gustaría saber interpretar el resultado de la constante de desintegración utilizando la actividad inicial en vez del número de átomos iniciales,por favor,¿es posible hacerlo de alguna forma inteligible?
Gracias!!
Raúl RC
el 8/1/19El calcular la constante de desintegración va a depender de los datos que te proporcione el problema en cuestión.
Te recomiendo por experiencia que te ciñas a la definición de este parámetro, el cual lo calculas haciendo la inversa de la vida media.
Para buscar la relacion con la actividad has de recordar que esta se define a su vez como A=λN siendo N el numero de nucleos de la muestra y teniendo en cuenta que:
N=N0·e^(-λt) obtienes que:
A=A0·e^(-λt)
Espero lo entiendas mejor ;)
umayuma
el 9/1/19Raúl RC
el 11/1/19Vayamos por partes:
1) La interpretación de λ se define por si misma, como la constante de desintegracion que hace referencia a la inversa de la vida media, pero también como aparece en una de las fotos que adjuntas esa constante se define como una probabilidad de desintegración de núcleos
2) Otra cosa es la actividad A que se puede relacionar con la vida media y el número de nucleos presentes en una muestra como A=λN, ahí es donde tienes la relacion que te interesa, ya que la actividad hace referencia al número de nucleos que se desintegran en un determinado tiempo.
Con lo cual lo que es correcto la definición que das en las imagenes, ya que la constante de desintegracion se puede definir como la inversa de la vida media o como la probabilidad de desintegrarse los nucleos de una muestra, de ahi que aparezca una derivada temporal, ya que es una tasa de velocidad de desintegracion de esos nucleos
Un saludo
-
Raúl RC
el 8/1/19Lamento no poder ayudarte pero no resolvemos dudas universitarias que no tengan que ver específicamente con los vídeos que ha grabado el profe como excepción, lo lamento.
Ojalá algún otro unico universitario pueda ayudarte, la idea sería que os ayudarais los unos a los otros