-
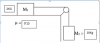
BUENAS UNICOOS!! ME PODEIS AYUDAR CON ESTE PROBLEMA? LO HE HECHO Y LA ACELERACION ME DA 7'92m/s2 Y LA TENSION 18'8 N. ESTA BIEN? MUCHAS GRACIAS. CALCULA LA ACELERACION DEL SISTEMA Y LA TENSION DE LA CUERDA. ATENCION!!! LOS DATOS SON: M1=2Kg M2=10Kg COEFICIENTE DE ROZAMIENTO= 0'15
Antonio Silvio Palmitano
el 6/1/19Observa que sobre el bloque apoyado actúan cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P1 = M1*g = 2*9.8 = 19,6 N, vertical hacia abajo,
Acción normal de la superficie: N1, vertical hacia arriba,
Tensión de la cuerda: T, horizontal hacia la derecha,
Rozamiento de la superficie: fr = μ*N = 0,15*N, horizontal hacia la izquierda.
Luego, aplicas la Segunda Ley de Newton y tienes el sistema de ecuaciones (observa que consideramos sentidos positivos hacia la derecha y hacia arriba):
N1 - P1 = 0, de aquí despejas: N1 = P1, y de aquí tienes: N1 = 19,6 N (1);
T - fr = M1*a, sustituyes expresiones, y queda: T - 0,15*N = 2*a,
aquí reemplazas el valor señalado (1), y queda: T - 0,15*19,6 = 2*a, y de aquí despejas: T = 2,94 + 2*a (2).
Observa que sobre el bloque colgado actúan dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: P2 = M2*g = 10*9.8 = 98 N, hacia abajo,
Tensión de la cuerda: T, vertical hacia arriba,
Luego, aplicas la Segunda Ley de Newton y tienes la ecuación (observa que consideramos sentido positivo hacia abajo):
P2 - T = M2*a, aquí reemplazas valores, y queda: 98 - T = 10*a, y de aquí despejas: T = 98 - 10*a (3).
Luego, sustituyes la expresión señalada (2) en la ecuación señalada (3), y queda:
2,94 + 2*a = 98 - 10*a, sumas 10*a y restas 2,94 en ambos miembros, y queda:
12*a = 95,06, divides por 12 en ambos miembros, y queda:
a ≅ 7,922 m/s;
luego, reemplazas este último valor remarcado en las ecuaciones señaladas (2) (3), y en ambas tienes:
T ≅ 18,783 N.
Por lo que tienes que tus resultados son correctos.
Espero haberte ayudado.
-
BUENAS TARDES UNICOOS! PORFAVOR NECESITO AYUDA CON ESTE PROBLEMA PORQUE NO HE ENCONTRADO AQUI NINGUN VIDEO QUE LO EXPLIQUE, POR FAVOR. MUCHAS GRACIAS DE NATEMANO Y PORFAVOR AYUDENME
El motor de un coche genera una fuerza motriz
de 4.500 N; la fuerza de rozamiento entre las ruedas
y la carretera es de 1.300 N. Si la masa del coche
es de 860 kg, determina:
a) La velocidad que alcanzará después de 10 s si parte
del reposo. Exprésala en km / h.
b) Si en este instante la fuerza del motor cesa, en cuanto
tiempo tardará en pararse?
Jerónimo
el 3/1/19Movimiento rectilíneo uniformemente acelerado Movimiento rectilíneo uniformemente acelerado
F-Fr=ma 4500-1300=860a a=3,72m/s2
v=vo+at=0+3,72*10=37,2m/s
Cuando cesa la F motor, sólo habrá Fr y la aceleración será -Fr=ma -1300=860a a=-1,51 m/s2
V=vo+at Como se para V=0 0=37,2-1,51t t=24,6m/s
cerin laissaoui
el 3/1/19 -
Hola, estoy totalmente perdida con este ejercicio lo he empezado a plantear pero la verdad no se si esta bien. Gracias
-
hola , he planteado este problema pero no me da la solución. Podrían ayudarme o guiarme un poco. Gracias
Antonio Silvio Palmitano
el 6/1/19Establece un sistema de referencia con eje de posiciones (alturas) OY vertical, con origen en el nivel del punto A, y con sentido positivo hacia arriba.
Luego, observa que tienes dos instantes importantes (inicial y final), para los que planteamos las expresiones de las energías potencial gravitatoria del collarín, cinética de traslación del collarín, y potencial elástica del resorte (observa que empleamos unidades internacionales):
Al inicio:
EPgi = 0,
ECti = 0,
EPei = (1/2)*k*Δs2 = (1/2)*24*(Li - L0)2 (1),
aquí observa el triángulo rectángulo cuya base mide 0,45 m, cuya altura mide 0,25+0,5 = 0,75 m, y cuya hipotenusa mide la longitud inicial del resorte, por lo que puedes plantear:
Li = √(0,452+0,752) = √(0,765) ≅ 0,875 m;
luego reemplazas este valor y el valor de la longitud inicial del resorte en la expresión señalada (1), y queda:
EPei ≅ (1/2)*24*(Li - L0)2 ≅ (1/2)*24*(0,875 - 0,275)2 ≅ (1/2)*24*(0,6)2 ≅ 4,32 J;
luego, planteas la expresión de la energía mecánica inicial del sistema resorte-collarín, y queda:
EMi = EPgi + ECti + EPei ≅ 0 + 0 + 4,32 ≅ 4,32 J.
Al final:
EPgf = M*g*yf = 0,9*9,8*0,25 = 2,205 J,
ECtf = (1/2)*M*vf2 = (1/2)*0,9*vf2 = 0,45*vf2 (en Joules),
EPef = (1/2)*k*Δs2 = (1/2)*24*(Lf - L0)2 = (1/2)*24*(0,5 - 0,275)2 = (1/2)*24*(0,225)2 = 0,6075 J;
luego, planteas la expresión de la energía mecánica final del sistema resorte-collarín, y queda:
EMf = EPgf + ECtf + EPef = 2,205 + 0,45*vf2 + 0,6075 = 2,8125 +0,45*vf2 (en Joules).
Luego, planteas conservación de la energía mecánica (observa que despreciamos todas las pérdidas por rozamientos), y queda la ecuación:
EMf = EMi, sustituyes expresiones, y queda:
2,8125 +0,45*vf2 ≅ 4,32, restas 2,8125 en ambos miembros, y queda:
0,45*vf2 ≅ 1,5075, divides por 0,45 en ambos miembros, y queda:
vf2 ≅ 3,35, extraes raíz cuadrada positiva en ambos miembros, y queda:
vf ≅ √(3,35) ≅ 1,830 m/s.
Espero haberte ayudado.
-
BUENAS! ME PODÉIS AYUDAR CON ESTE ESQUEMA? HAY VIDEOS UNICOOS QUE EXPLIQUEN ESTE TEMA? MUCHAS GRACIAS
Realiza un esquema donde queden representadas,
mediante vectores, las fuerzas que actúan sobre
un cuerpo que desciende por un plano inclinado. considera
que existe rozamiento entre el cuerpo y el plano.
Antonio Silvio Palmitano
el 5/1/19Observa que sobre el cuerpo actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo;
Acción normal del plano inclinado: N, perpendicular al plano inclinado, hacia arriba;
Rozamiento del plano inclinado: fr = μ*N, paralela al plano inclinado, hacia arriba.
Queda que hagas el gráfico correspondiente, y recuerda que si debes plantear un problema completo, es conveniente que establezcas un sistema de referencia OXY, con eje OX paralelo al plano inclinado con sentido positivo hacia abajo (que es el sentido de desplazamiento del cuerpo), y con eje OY perpendicular al plano inclinado con sentido positivo hacia arriba.
Espero haberte ayudado.
-
BUENAS! QUE RESPUESTA ELEGIRIAIS? YO CREO QUE LA C, PERO ME LO PODEIS CONFIRMAR Y EL POR QUE? MUCHAS GRACIAS DE ANTEMANO UNICOOS!!
Elige la respuesta correcta. Cuando tienes un libro
en la mano:
a) No se ejerce ninguna fuerza, porque no se mueve.
b) Las fuerzas que se ejercen tienen el único efecto
de deformarlo.
c) Las fuerzas que se ejercen tienen una resultante
nula, por lo que no se mueve.
d) Ninguna de las respuestas es correcta.
-
BUENAS!! EN ESTA PREGUNTA HE MARCADO LA OPCION D. ESTA BIEN?
Si un tren se mueve por la vía a una velocidad de 60 km / h,
indica cuál de las siguientes afirmaciones es correcta:
a) Sobre el tren no actúa ninguna fuerza porque
no hay aceleración.
b) Sobre el tren sólo actúa una fuerza, en la misma
dirección que la velocidad.
c) Sobre el tren actúan varias fuerzas, la resultante
de las cuales es nula.
d) Sobre el tren actúan diversas fuerzas la resultante
de las que proporciona la velocidad del tren.
-
BUENAS TARDES UNICOOS! AYUDENME PORFAVOR EN ESTE PROBLEMA PORQUE NO LOGRO ENTENDERLO. MUCHAS GRACIAS DE ANTEMANO!!
Sobre un cuerpo de 700 g de masa apoyado en una mesa
horizontal se aplica una fuerza de 5N en la dirección
del plan. Calcula la fuerza de rozamiento si:
a) El cuerpo adquiere una aceleración igual a 1,5 m / s2
.
b) El cuerpo se mueve a una velocidad constante.
Antonio Silvio Palmitano
el 3/1/19Observa que sobre el cuerpo actúan cuatro fuerzas de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g = 0,7*9,8 = 6,86 N, vertical hacia abajo,
Acción normal de la mesa: N, vertical hacia arriba,
Fuerza exterior: F = 5 N, horizontal hacia la derecha,
Rozamiento dinámico: fr, horizontal hacia la izquierda:
a)
Aplicas la Segunda Ley de Newton (consideramos positivo hacia la derecha y hacia arriba), y queda:
F - fr = M*a,
N - P = 0;
sustituyes expresiones, y queda:
5 - fr = 0,7*1,5, de aquí despejas: fr = 5 - 0,7*1,5, resuelves y queda: fr = 3,95 N,
N - 6,86 N = 0, de aquí despejas: N = 6,86 N.
b)
Aplicas la Primera Ley de Newton (consideramos positivo hacia la derecha y hacia arriba), y queda:
F - fr = 0,
N - P = 0;
sustituyes expresiones, y queda:
5 - fr = 0, de aquí despejas: fr = 5 N,
N - 6,86 N = 0, de aquí despejas: N = 6,86 N.
Espero haberte ayudado.
cerin laissaoui
el 3/1/19 -
Hola, tengo dudas en como establecer el principio de conservación de energía sobre todo en la primera parte del problema. Lo he intentado hacer pero no coinciden las soluciones.Podrian ayudarme.Muchas gracias
Antonio Silvio Palmitano
el 3/1/19Considera un sistema de referencia con eje de posiciones (alturas) OY vertical con sentido positivo hacia arriba, con origen de coordenadas al nivel del extremo del muelle relajado.
Llamamos h a la distancia entre el centro de masas del cilindro y su base, y llamamos Δs a la compresión del muelle.
Luego, observa que tienes tres instantes importantes:
1)
El cilindro inicia su caída, y aquí tienes:
y1 = h + 100 mm = h + 0,1 m, de donde tienes: EPg1 = M*g*y1 = 5*9,8*(h + 0,1) = 49*(h + 0,1) (en Joules),
v1 = 0, de donde tienes: EC1 = (1/2)*M*v12 = (1/2)*5*02 = 0,
Δs1 = 0, de donde tienes: EPe1 = (1/2)*k*02 = (1/2)*1800*02 = 0;
luego, planteas la expresión de la energía mecánica total, y queda:
EM1 = EPg1 + EC1 + EPe1 = 49*(h + 0,1) + 0 + 0 = 49*(h + 0,1) (en Joules).
2)
El cilindro está a punto de tocar el extremo del muelle, y aquí tienes:
y2 = h, de donde tienes: EPg2 = M*g*y2 = 5*9,8*h = 49*h (en Joules),
v2 = a determinar, de donde tienes: EC2 = (1/2)*M*v22 = (1/2)*5*v22 = (5/2)*v22 (en Joules),
Δs2 = 0, de donde tienes: EPe2 = (1/2)*k*02 = (1/2)*1800*02 = 0;
luego, planteas la expresión de la energía mecánica total, y queda:
EM2 = EPg2 + EC2 + EPe2 = 49*h + (5/2)*v22 + 0 = 49*h + (5/2)*v22 (en Joules).
3)
El cilindro ha comprimido al muelle, y aquí tienes:
y3 = -x, de donde tienes: EPg3 = M*g*y3 = 5*9,8*(h - x) = 49*(h - x) (en Joules),
v3 = 0, de donde tienes: EC3 = (1/2)*M*v32 = (1/2)*5*02 = 0,
Δs3 = -x, de donde tienes: EPe3 = (1/2)*k*Δs32 = (1/2)*1800*(-x)2 = 900*x2 (en Joules);
luego, planteas la expresión de la energía mecánica total, y queda:
EM3 = EPg3 + EC3 + EPe3 = 49*(h - x) + 0 + 900*x2 = 49*(h - x) + 900*x2 (en Joules).
a)
Planteas conservación de la energía entre los instantes (3) y (1), y queda:
EM3 = EM1, sustituyes expresiones, y queda:
49*(h - x) + 900*x2 = 49*(h + 0,1), distribuyes los factores comunes, y queda:
49*h - 49*x + 900*x2 = 49*h + 4,9, restas 49*h y restas 4,9 en ambos miembros, y queda:
-49*x + 900*x2 - 4,9 = 0, ordenas términos, y queda:
900*x2 - 49*x - 4,9 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
a1)
x = ( 49 - √(20041) )/1800 ≅ -0,051426 m,
que no tiene sentido para este problema (observa que x representa una longitud),
a2)
x = ( 49 + √(20041) )/1800 ≅ 0,105870 m,
por lo que puedes concluir que el resorte se comprime 105,870 mm aproximadamente.
b)
Planteas conservación de la energía entre los instantes (3) y (1), y queda:
EM2 = EM1, sustituyes expresiones, y queda:
49*h + (5/2)*v22 = 49*(h + 0,1), distribuyes el factor común, y queda:
49*h + (5/2)*v22 = 49*h + 4,9, restas 49*h en ambos miembros, y queda:
(5/2)*v22 = 4,9, multiplicas por 2 y divides por 5 en ambos miembros, y queda:
v22 = 1,96, extraes raíz cuadrada positiva en ambos miembros, y queda:
v2 = 1,4 m/s,
por lo que puedes concluir que la máxima rapidez que alcanza el cilindro es 1,4 m/s.
Espero haberte ayudado.