-
Hola buenas tengo dudas con un ejercicio, me dan los valores dd las cargas q1=3*10^-3 y q2=12*10^-6 ambas cargas estan separadas 20 cm y estan situadas en los puntos A y B respectivamente. Me pide:
A) razone como varía el campo electrico entre A y B y representar graficamente la variacion en funcion al punto A.
B) Calcular el punto donde el campo electrico sea nulo.
En el apartado B me da 0'13m a la izquierda de la carga q2 pero cuando lo hicimos en clase dio un numero diferente.
ANTONIO MONTERO
el 2/1/19Es un problema de física algo confuso debido a la notación científica.
Su error fue dividir las cargas entre 3 para simplificar el ejercicio, ya que no se dio cuenta de que el elevado (-3) y (-6) no era el mismo.
Aquí le dejo una foto del apartado B resuelto.
Espero que le sea de ayuda.
Cabe destacar que comprobé los resultados de la igualdad y son prácticamente iguales, debido a no poner todos los decimales.
Antonio Silvio Palmitano
el 2/1/19Observa el gráfico, y verás que ubicamos el origen de coordenadas en el punto A, y que la abscisa del punto B es 0,2 m.
Luego, considera el punto genérico P, cuya abscisa hemos indicado con x, y observa que en él tienes dos campos electrostáticos, cuyas direcciones están sobre el eje OX, y cuyos módulos y sentidos indicamos:
E1 = k*q1/x2, hacia la derecha (observa que la carga q1 es positiva),
E2 = k*q2/(0,2-x)2, hacia la izquierda (observa que la carga q1 es positiva).
Luego, planteas la expresión del campo resultante para puntos situados en el eje OX (presta atención a los sentidos de los campos, y queda:
E(x) = E1 - E2, sustituyes expresiones, y queda:
E(x) = k*q1/x2 - k*q2/(0,2-x)2;
luego, reemplazas valores, y queda:
E(x) = 9*109*3*10-3/x2 - 9*109*12*10-6/(0,2-x)2,
resuelves coeficientes, y queda:
E(x) = 27*106/x2 - 108*103/(0,2-x)2 (respuesta al primer inciso).
Luego, planteas la condición de campo resultante nulo, y queda:
E(x) = 0, sustituyes la expresión remarcada en el primer miembro, y queda:
27*106/x2 - 108*103/(0,2-x)2 = 0,
divides por 27*103 en todos los términos, y queda:
103/x2 - 4/(0,2-x)2 = 0,
sumas 4/(0,2-x)2 en ambos miembros, y queda:
103/x2 = 4/(0,2-x)2,
multiplicas por x2 y por (0,2-x)2 en ambos miembros, y queda:
103*(0,2-x)2 = 4*x2,
resuelves el coeficiente y desarrollas el binomio elevado al cuadrado en el primer miembro, y queda:
1000*(0,04 - 0,4*x + x2) = 4*x2,
distribuyes el primer miembro, restas 4*x2 en ambos miembros, y queda:
40 - 400*x + 996*x2 = 0,
divides por 4 en todos los términos, ordenas términos, y queda:
249*x2 - 100*x + 10 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
1°)
x = ( 100 + √(40) )/(2*249) ≅ 0,214 m,
que no tiene sentido para este problema, porque corresponde a un punto ubicado a la derecha del punto B, en el cuál los dos campos tienen sentido hacia la derecha;
2°)
x = ( 100 - √(40) )/(2*249) ≅ 0,188 m,
que sí tiene sentido para este problema, porque corresponde a un punto ubicado entre el punto A y el punto B, en el cuál los dos campos tienen sentidos contrarios.
Luego, puedes concluir que el punto P está ubicado aproximadamente a 0,188 m a la derecha del punto A,
lo que corresponde a 0,012 m a la izquierda del punto B.
Espero haberte ayudado.
-
Una duda para aclarar: La pregunta 10 seleccione la A; basandome en un articulo de internet. Alguien me podria ayudar en esta aclaracion
Raúl RC
el 1/1/19Antonio Silvio Palmitano
el 2/1/19Vamos con una precisión.
Considera la expresión de la resistencia en función de la temperatura (con mucha frecuencia, se considera que la temperatura de referencia es: Tr = 20 °C, para la que corresponde la resistencia de referencia del material: Rr, cuyo valor depende del material que se esté estudiando:
R(T) = Rr*( 1 + α*(T - Tr) ) (1).
Luego, observa que el coeficiente de temperatura del material (α), la resistencia de referencia (Rr) y la temperatura de referencia (Tr) son constantes, por lo que tienes que la resistencia es una función que depende solamente de la temperatura, y siempre y cuando ésta no tome valores mucho mayores que la temperatura de referencia.
Luego, puedes concluir que si la temperatura permanece constante entonces también permanece constante la resistencia del material por lo que la opción señalada (B) es la respuesta correcta.
Luego, observa que si distribuyes el factor común Rr entre los términos del agrupamiento, entonces queda:
R(T) = Rr + Rr*α*(T - Tr), aquí restas Rr en ambos miembros, y queda:
R(T) - Rr = Rr*α*(T - Tr),
y observa que en el primer miembro tienes la expresión de la variación de la resistencia,
y que en el segundo tienes los factores constantes Rr y α que multiplican a la variación de la temperatura,
por lo que tienes que la variación de la resistencia es directamente proporcional a la variación de la temperatura.
Espero haberte ayudado.
-
Jerónimo
el 1/1/19A partir de la imagen, para un conductor no óhmico en el que la relación entre V e I no es lineal, (no cumple la Ley de Ohm) vemos que R es la pendiente de ΔV sobre ΔI, pero la gráfica de tu ejercicio está representada al revés , por tanto la respuesta sería D) 1/pendiente.
11 c)
-
Hola buenas feliz año, tengo una duda con el ejercicio 5
 no puedo calcular la energia potencial en el punto de origen ya que no tengo una distancia asiq solo se me ocurre considerar que la Ep en el origen es 0 pero no se si es correcto
no puedo calcular la energia potencial en el punto de origen ya que no tengo una distancia asiq solo se me ocurre considerar que la Ep en el origen es 0 pero no se si es correctoAntonio Silvio Palmitano
el 1/1/19Tienes el valor de la carga puntual:
q = 6*10-6 C.
Tienes el valor del módulo del campo electrostático:
|E| = 500 N/C,
cuya expresión vectorial es:
E = < 0 , 500 >.
a)
Luego, planteas la expresión vectorial de la fuerza ejercida sobre la carga, y queda:
F = q*E, sustituyes expresiones, y queda:
F = 6*10-6*< 0 , 500 >, resuelves la multiplicación, y queda:
F = < 0 , 3*10-3 >, cuyo módulo queda:
|F| = 3*10-3 N;
luego, si designas con M a la masa de la partícula cargada, aplicas la Segunda Ley de Newton, y tienes la ecuación vectorial:
a = F/M, sustituyes la expresión de la fuerza, y queda:
a = < 0 , 3*10-3 > / M (en m/s2),
y observa que la aceleración es constante, que tiene la dirección y sentido positivo del eje OY,
por lo que puedes concluir que la partícula se desplaza con Movimiento Rectilíneo Uniformemente Acelerado con la dirección y el sentido que hemos indicado.
Luego, planteas la expresión del trabajo realizado por la fuerza electrostática (observa que es constante, y que es paralela al desplazamiento y con su mismo sentido, con posición inicial: < 0 , 0 > y posición final: < 0 , 2 >), y queda:
WF = F•Δs, sustituyes expresiones, y queda:
WF = < 0 , 3*10-3 >•< 0-0 , 2-0 >, resuelves componentes en el segundo factor, y queda:
WF = < 0 , 3*10-3 >•< 0 , 2 >, desarrollas el producto escalar, y queda:
WF = 0*0 + 3*10-3*2, resuelves, y queda:
WF = 6*10-3 J;
luego, planteas la definición de la variación de energía potencial electrostática, y queda:
ΔEP = - WF, reemplazas el valor del trabajo de la fuerza electrostática en el segundo miembro, y queda:
ΔEP = -6*10-3 J,
y como el resultado es negativo, tienes que la energía potencial ha disminuido,
y observa que hemos calculado la variación de energía potencial electrostática independientemente de sus valores específicos en el punto inicial y en el punto final de la trayectoria de la partícula.
b)
Planteas la definición de variación del potencial electrostático, y queda:
ΔV = ΔEP/q, reemplazas valores, y queda:
ΔV = -6*10-3/ 6*10-6, resuelves, y queda:
ΔV = -103 V,
y como el resultado es negativo, tienes que el potencial ha disminuido,
y observa que hemos calculado la variación del potencial electrostático independientemente de sus valores específicos en el punto inicial y en el punto final de la trayectoria de la partícula.
Espero haberte ayudado.
-
hola... me ayudan con estos dos problemas por favor:
Problema 1:
Dos puntos móviles "A" y "B" están separados en 4005 m; "A" detrás de "B". En el mismo instante y con la misma dirección y sentido parten, "A" con rapidez constante de 72 km/h y "B" con M.R.U.V. de 0.04 m/s2. Se pide calcular :
a) ¿A qué distancia de la partida de "B" se encuentran?
b) ¿Qué tiempo transcurre?
c)La rapidez del móvil "B" en el momento del encuentro
Problema 2:
Un móvil con velocidad "v" m/s es frenado desacelerando a razón de "a" m/s2 ¿Qué espacio recorrió en el antepenúltimo segundo?
Fernando Alfaro
el 1/1/19Problema 1:
La ecuación de posición de un MRU es: x(t) = vt + x0 y la ecuación de posición de un MRUV es: x(t) ½at2 + v0t+ x0
Si la posición inicial del móvil a es x0A = 0m entonces, la posición inicial del móvil B es x0B = 4005 m
La velocidad del móvil A es v = 72km/h = 20m/s y la velocidad inicial del movil B (asumo que parte del reposo) es v0B = 0
Las ecuaciones de los movimientos son entonces: xA(t) = vt = 20t y xB(t) = ½at + x0B = 0.02t2 + 4005
Los móviles se encuentran cuando sus posiciones son iguales, es decir, xA = xB
Igualando las ecuaciones: 20t = 0.02t2 + 4005 => 0.02t2 - 20t + 4005 = 0 => t = ( 20 ± √(202 - 4*0.02*4005) ) / (2*0.02) = ( 20 ± √(400 - 320.4)) /0.04 =>
t = (20±√79.6) / 0.04 => t1 = 11.08/0.04 = 276.9 s y t2 = 28.92/0.04 = 723 s (respuestas de la parte b)
Ambas respuestas son validas, los móviles se encuentran por primera vez en t1 , el móvil A rebasa al móvil B, y como el móvil B sigue acelerando y el móvil A no, se vuelven a encontrar en t2
Se encuentran por primera vez, en la posición x(t1). Sustituyendo en la ecuación del móvil A: xA(276.9) = 20*276.9 = 5538 m
Pero el móvil B parte de la posición 4005, medido desde la posición inicial de B se encuentran entonces en: 5538 - 4005 = 1533m (respuesta de la parte a)
La ecuación de velocidad de un MRUV es: v(t) = at + v0 Como a = 0.04 y v0 = 0 => vB(t) = 0.04t
En t = 276.4, vB(276.4) = 0.04*276.4 = 11.08 m/s (respuesta a la parte c)
Fernando Alfaro
el 1/1/19El problema 2 es algo ambiguo. La desaceleración "a" es constante? Cual es el "último" instante de tiempo? El "ultimo" instante es cuando la velocidad es 0?
Si me respondes esas preguntas quizás pueda dar una respuesta un poco mas especifica.Respondiendo en términos generales.
La distancia recorrida en un intervalo de tiempo [a,b] es: x = ∫v(t)dt con limites de integración [a,b]
Si k es el ultimo instante de tiempo, el último segundo transcurre entre k -1 y k, el penúltimo segundo entre k-2 y k-1 y el antepenúltimo entre k-3 y k-2
La distancia recorrida en el antepenúltimo intervalo de 1 segundo es entonces, x = ∫v(t)dt entre [k-3, k-2]
La función v(t) es: v(t) = ∫a(t)dt (integral indefinida) y sustituyendo v(t) en la ec de posición:
x = ∫ (∫ a(t) dt) dt, con limite de integración entre [k-3,k-2], donde k es el "ultimo" instante de tiempo.
(Nota: En realidad son todos desplazamientos, el espacio recorrido técnicamente es la integral sin signo.)
V. Rod.
el 2/1/19V. Rod.
el 5/1/19Fernando Alfaro
el 6/1/19Llego a la respuesta que tu dices suponiendo una desaceleración constante de modulo "a" y haciendo la pregunta: ¿Qué espacio recorrió desde el antepenúltimo segundo hasta el momento que se detiene? (y definiendo el ultimo instante de tiempo en el momento en que se detiene)
Como la desaceleración es constante es un MRUV y las ecuaciones de posición y velocidad son:
x(t) = -½at2 + vt + x0 y v(t) = -at + v Donde "a" es el modulo de la desaceleración, "v" es la velocidad inicial y "x0" la posición inicial.
El instante de tiempo en el que se detiene se calcula igualando la ec de velocidad a 0, v(t) = 0 y despejando t:
v(t) = 0 => -at + v = 0 => -at = -v => t = v/a Lamemosle tf a v/a.
Por lo tanto el intervalo de tiempo que transcurre desde el antepenúltimo segundo hasta el momento que se detiene es: [tf - 3 , tf]
El espacio recorrido, técnicamente es la suma de los desplazamientos en valor absoluto, es decir, desplazamientos siempre considerados positivos. Si el desplazamiento cambia de signo en el intervalo de tiempo hay que aplicar valor absoluto. Para evaluar si el desplazamiento cambia de signo hay que estudiar el signo de la función de la velocidad. Puedes hacerlo si quieres, pero te prometo que en el intervalo [tf - 3, tf ] la velocidad no cambia de signo, y el espacio recorrido es el modulo del desplazamiento. Dicho esto:
El desplazamiento se puede calcular por integración, calculando la integral definida: Δx = ∫v(t)dt con limites [tf - 3 , tf ]
O por la formula: Δx = xf - xi Calculando las posiciones xf y xi a partir de la ec de posición de un MRUV con tf y ti respectivamente.
Por el método: Δx = xf - xi
En nuestro caso, tf = v/a y ti = tf - 3 = v/a - 3
Sustituyendo los valores en la ec de posición podemos calcular xf y xi :
xf = x(tf) = -½atf2 + vtf + x0 = -½a(v/a)2 + v(v/a) + x0 = -½ v2/a + v2/a + x0
xi = x(ti) = ½ati2 + vti + x0 = -½ a(v/a -3)2 + v (v/a - 3) + x0 = -½a (v2/a2 - 6v/a + 9) + v2/a - 3v + x0 = -½ v2/a + 3v - 9/2 a + v2/a -3v + x0 = -½ v2/a - 9/2 a + v2/a + x0
Y restando xf y xi :
Δx = xf - xi = -½ v2/a + v2/a + x0 - (-½ v2/a - 9/2 a + v2/a + x0) = -½ v2/a + v2/a + x0 + ½ v2/a + 9/2 a - v2/a - x0 = 9/2 a
Supuse varias cosas para llegar a la respuesta pero espero haberte ayudado en algo.
-
Fernando Alfaro
el 31/12/18Ej 6. P = V*I y V = I*R
Ambas resistencias están conectadas en paralelo a la misma fuente de modo que tienen la misma diferencia de potencial V.
Para que la segunda resistencia disipe 4 veces mas potencia que la primera, debe circular por ella 4 veces mas intensidad.
Y para que circule 4 veces mas intensidad a la misma diferencia de potencial, la resistencia debe ser 4 veces menor, es decir R/4
Ej 12
Respuesta: A. W El motivo, campo magnético alrededor de un hilo, regla de la mano derecha.
Antonio Silvio Palmitano
el 31/12/1812)
Para determinar cuál es el vector que representa la dirección y el sentido del campo magnético en el punto P debes aplicar la "Regla de la Mano Derecha", y para ello considera los siguientes pasos:
1°)
Tranza una circunferencia con centro en el punto en el que el hilo conductor corta al plano del papel (observa que tienes señalado este punto con una cruz rodeada con una circunferencia pequeña), y que pase por el punto en estudio P.
2°)
Con el dedo pulgar de tu mano derecha señala el sentido de la corriente (observa que en este caso es "entrante" al plano del papel).
3°)
Gira los demás dedos de tu mano manteniendo quieto el pulgar, y tendrás el sentido de giro del campo magnético alrededor del hilo de la corriente;
observa que este giro es horario, por lo que tienes que el vector señalado W es es que representa la dirección y el sentido del campo magnético B producido por la corriente conducida por el hilo en el punto P.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 31/12/18Observa que como las resistencias (R1, y R2) están conectadas en paralelo, entonces tienes que la tensión suministrada por la fuente de alimentación es la misma para las dos (V).
Luego, planteas la expresión de la potencia disipada por cada dispositivo en función de la tensión (observa que es la misma para los dos dispositivos) y de su resistencia, y tienes las ecuaciones:
P1 = V2/R1, aquí multiplicas por R1 en ambos miembros, y queda: P1*R1 = V2 (1);
P2 = V2/R2, aquí multiplicas por R2 en ambos miembros, y queda: P2*R2 = V2 (2).
Luego, igualas las expresiones señaladas (2) (1), y queda:
P2*R2 = P1*R1,
aquí divides por x en ambos miembros, y queda:
R2 = P1*R1/R2,
sustituyes las expresiones de las potencias de los dos dispositivos (P1 = P, P2 = 4*P), y de la resistencia del primero de ellos que tienes en tu enunciado, (R1 = R), y queda:
R2 = P*R / (4*P),
simplificas, y queda:
R2 = R/4.
Espero haberte ayudado.
-
Hola muy buenas, gracias por estar siempre solucionando nuestras dudas, se lo agradezco mucho a todos. Tengo una pregunta en un apartado y no he conseguido solucionarlo.
Únicamente es el apartado C. Los otros dos apartados los he conseguido solucionar. El problema es que no entiendo porque da 0 ni como podría llegar a esa conclusión. Haciendo el menos incremento de Ep me quedé pillado y no supe avanzar. Muchas gracias de antemano.
Jerónimo
el 30/12/18El Campo Gravitatorio es un campo de fuerzas centrales ,también llamado conservativo, ésto quiere decir que la energía potencial sólo depende de la distancia al centro (fuente del campo). Si te fijas el punto (6,0) y el punto (0,6) están a la misma distancia del centro, por lo que tendrán la misma energía potencial EpA=EpC y como W=-ΔEp =0
-
Jerónimo
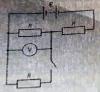
el 31/12/18Antes de cerrar el circuito , las dos resistencias de arriba están en serie y la fem se reparte por igual , el voltímetro marcará ε/2.
Al cerrar el circuito cambia la configuración estando las dos resistencias de arriba en paralelo y en serie con la tercera.
Calculando la resistencia equivalente Req: 1/R¨=1/R+1/R=2/R R¨=R/2 Requivalente=R¨+R=R/2+R= 3R/2
La intensidad total será I=ε/Req=2ε/3R y la fem que marcára el voltímetro =IR¨=2ε/3R *R/2= ε/3
-
Buenas, necesitaría ayuda con la siguiente pregunta:
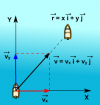
Un nadador intenta cruzar perpendicularmente un rio nandando con una velocidadde 1.6 m/s respecto al agua, la velocidad de la corriente es 0.8 m/s hacia el Este,el río tiene una anchura de 80m.
a) Calcula la velocidad del nadador respecto a la orilla.
b)La distancia que ha recorrido el nadador al cruzar el río.
-
Jerónimo
el 30/12/18Llamamos x a la longitud total recorrida. El movimiento de Josie es siempre a v cte x=vj*tf
El recorrido de Josie tiene dos partes, x1 acelerando y x2 frenando siendo x=x1+x2
Usando la ecuación del MUA x=1/2 at²
1º parte: (Acelerando) a=Δv/Δt=(vm-vo)/(tf-to)=vm/tf pues vo=0 m/s y to=0s
x1=1/2 (vm*tm)
2º parte: (Frenando) a= Δv/Δt=(vf-vm)/(tf-tm)= -vm/(tf-tm) vf=0 m/s .En este movimiento hay velocidad inicial (MUA) x=vot+1/2mv² quedando:
x2=vm(tf-tm)-1/2vm*(tf-tm)=1/2vm(tf-tm)
Como x=x1+x2 vj*tf=1/2 (vm*tm)+1/2vm*(tf-tm)=1/2vm*tm+1/2vm*tf-1/2vm*tm
vj=1/2vm