-
BUENAS DE NUEVO! EN UN GRÁFICO v-t, COMO SE CALCULA LA VELOCIDAD? MUCHISIMAS GRACIAS DE ANTEMANO UNICOOS!
Francisco Javier Tinoco Tey
el 3/1/19Si se trata de un MRU la ecuacion es la siguiente:
Δx= v•t
Si se trata de un MRUA la ecuacion es la siguiente:
vf=vo+a•t
Si tienes dudas en la obtención de las ecuaciones puedes obtenerla fácilmente realizando una grafica, por ejemplo para el movimiento rectilíneo uniforme sabes que la grafica con respecto al tiempo es una recta.
-
BUENAS UNICOOS! ESTE EJERCICIO LO HE RESUELTO POR MI MISMA PERO TENGO PROBLEMOS EN EL APARTADO C ( LA VELOCIDAD EN EL TRAMO A) ME DA 5M/S Y EN EL TRAMO C) ME DA -10M/S PERO NO ESTOY SEGURA DE HABERLO HECHO BIEN). ME LO PODEIS CONFIRMAR Y AYUDARME CON EL C)? MUCHAS GRACIAS!!!
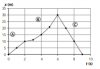
En la gráfica x-t siguiente, x está expresada en m, y t, en s. Interpreta el movimiento realizado por el móvil cada tramo y determina:
a) La velocidad en los tramos A y C.
b) El tipo de movimiento en el tramo B.
c) El espacio total recorrido.
Antonio Silvio Palmitano
el 3/1/19a)
En el tramo A tienes Movimiento Rectilíneo Uniforme.
Observa que la gráfica es un segmento que comienza en el punto (0,0) y termina en el punto (2,10),
por lo que planteas la expresión de la velocidad del móvil, y queda:
va = (10-0)/(2-0) = 10/2 = 5 m/s;
luego, planteas la expresión de la posición en función del tiempo de Movimiento Rectilíneo Uniforme (observa que reemplazamos las coordenadas del punto inicial del tramo), y queda:
x = 0 + 5*(t-0), cancelas términos nulos, y queda:
x = 5*t, con 0 ≤ t ≤ 2.
Observa que la gráfica es un segmento que comienza en el punto (6,30) y termina en el punto (9,0),
por lo que planteas la expresión de la velocidad del móvil, y queda:
vc = (0-30)/(9-6) = -30/3 = -10 m/s;
luego, planteas la expresión de la posición en función del tiempo de Movimiento Rectilíneo Uniforme (observa que reemplazamos las coordenadas del punto inicial del tramo), y queda:
x = 30 - 10*(t-6), con 6 ≤ t ≤ 9.
b)
Observa que el tramo B aparenta ser un tramo de parábola, que pasa por los puntos (2,10), (4,15) y (6,30),
por lo que puedes plantear la expresión de la posición en función del tiempo de Movimiento Rectilíneo Uniformemente Variado (observa que reemplazamos las coordenadas del punto inicial del tramo), y queda:
10 + vi*(t-2) + (1/2)*a*(t-2)2 = x (*),
reemplazas las coordenadas de los otro dos puntos, resuelves coeficientes, y queda:
luego, reemplazas las coordenadas de los puntos indicados, resuelves y queda el sistema de dos ecuaciones con dos incógnitas:
10 + 2*vi + 2*a = 15,
10 + 4*vi + 8*a = 30,
restas 10 en ambos miembros de las dos ecuaciones, divides por 2 en todos los términos de la segunda, y queda:
2*vi + 2*a = 5,
2*vi + 4*a = 10,
resuelves el sistema, y queda:
a = 2,5 m/s2, vi = 0;
luego, planteas nuevamente la expresión de la función posición para este tramo, y queda:
x = 10 + 0*(t-2) + (1/2)*2,5*(t-2)2, cancelas el término nulo, resuelves coeficientes, y queda:
x = 10 + 1,25*(t-2)2, con 2 ≤ t ≤ 6.
c)
Planteas la expresión general del desplazamiento del móvil en función de su posición inicial y de su posición final, y queda:
Δx = xf - xi;
luego, con las posiciones iniciales y finales de cada tramo, planteas las expresiones de los desplazamientos, y queda:
ΔxA = 10 - 0 = 10 m (observa que el signo positivo indica que el móvil se aleja del origen de coordenadas),
ΔxB = 30 - 10 = 20 m (observa que el signo positivo indica que el móvil se aleja del origen de coordenadas),
ΔxC = 0 - 30 = -30 m (observa que el signo negativo indica que el móvil se acerca al origen de coordenadas);
luego, planteas la expresión del desplazamiento total, y queda:
Δx = ΔxA + ΔxB + ΔxC = 10 + 20 + (-30) = 0,
y observa que este resultado es consistente, porque tanto la posición inicial como la posición final del móvil tiene el valor x = 0;
luego, como la posición del móvil siempre es positiva en todo instante, planteas que la distancia recorrida es igual a la suma de los valores absolutos de los desplazamientos, y queda:
d = |ΔxA| + |ΔxB| + |Δxc| = |10| + |20| + |-30| = 10 + 20 + 30 = 60 m.
Espero haberte ayudado.
-
BUENOS DIAS! TENGO EL SIGUIENTE PROBLEMA:
Un coche que circula a una velocidad de 108 km / h frena uniformemente y se detiene en 10 s. Encuentra la aceleración y el espacio que recorre hasta que se para.
LA ACELERACION LA HE CALCULADO Y ME DA -3m/s 2, PERO A LA HORA DE CALCULAR EL ESPACIO RECORRIDO ( X=Xo +Vo*T+1/2*a*t2) TENGO PROBLEMAS. GRACIAS DE ANTEMANO!
-
Hola! Me podriais decir las formulas para el espacio recorrido y el desplazamiento en un gráfico
posición- tiempo de un MRU???
Francisco Javier Tinoco Tey
el 2/1/19Xf = Xo+ v•t
a = 0
v = vo = cte
- x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
- v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s)
- a: La aceleración del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2)
-
5. Un chico y una chica están patinando sobre hielo unidos por una cuerda. El chico de 60 kg de masa, ejerce una fuerza sobre la chica de 10 N; la masa de la chica es de 40 kg: a. ¿Cuál es la aceleración que el chico comunica a la chica? b. ¿Qué fuerza actúa sobre el chico? Razona tu respuesta ¿Y qué aceleración sufre?
Me ha dado esto. a) 1/4 m/s2; b) 10 N(3ºA ley de Newton) 1/6 m/s2 Estaría bien? Gracias de antemano.
Guillem De La Calle Vicente
el 3/1/19El enunciado está un poco mal escrito. No se dice que la cuerda esté tensa, por lo que no tiene porque estar ejerciendo una fuerza sobre ninguno.
a) La única fuerza que actúa sobre la chica es la que ejerce el chico. Por lo tanto, por la Segunda Ley de Newton:
F = m_B * a --> a = F/m_B = 10/40 = 0,25 m/s².
b) Si la cuerda no está tensa, la chica ejerce la misma fuerza sobre el chico, 10 N por la tercera ley de Newton (principio de acción-reacción); y su aceleración es de a = 10/60 = 0,17 m/s².
Para el apartado a) no importa si la cuerda está o no tensa. Para el b) si. Te paso el apartado b) en el caso de que la cuerda esté tensa.
Saludos.
-
Alguien me puede ayudar
Se lanza una piedra verticalmente hacia arriba desde lo alto de un edificio de 80 m de forma que cae a la calle (V0=20 m/s)
a) Velocidad de la piedra al llegar al suelo.
b) Tiempo total de recorrido
c) Posición y velocidad a los 3 segundos de lanzamiento.
-
He intentado realizar el siguiente ejercicio mediante el Principio de la Conversación de la Energía Mecánica, teniendo el cuenta el trabajo del rozamiento. Pero, no estoy muy seguro de cómo se haría. Espero que me puedan ayudar.
Un saludo.
Antonio Silvio Palmitano
el 6/1/19Vamos con la primera etapa (movimiento horizontal).
Observa que la única fuerza que actúa en la dirección de desplazamiento es la fuerza de rozamiento, y observa además que esta fuerza no es constante, por lo que aplicas la Segunda Ley de Newton, y queda:
M*a(x) = -fr, sustituyes la expresión de la fuerza de rozamiento, y queda:
M*a(x) = -β*(L2 - x2)*M*g, divides por M en ambos miembros, y queda
a(x) = -β*(L2 - x2)*g, expresas a la aceleración como función de la velocidad y de la posición, y queda:
v(x)*dv/dx = -β*(L2 - x2)*g, ordenas factores en el segundo miembro, separas variables, y queda:
v(x)*dv = -β*g*(L2 - x2)*dx, multiplicas por 2 en ambos miembros, y queda:
2*v(x)*dv = -2*β*g*(L2 - x2)*dx, integras en ambos miembros, y queda:
v(x)2 = -2*β*g*(L2*x - (1/3)*x3) + C (1),
que es la expresión general del cuadrado de la velocidad de móvil en función de su posición;
luego, reemplazas los valores de la condición inicial: v(0) = v0, resuelves el segundo miembro, y queda:
v02 = C,
sustituyes esta expresión en la expresión señalada (1), ordenas términos, y queda:
v(x)2 = v02 - 2*β*g*(L2*x - (1/3)*x3) (1*),
que es la expresión del cuadrado de la velocidad del móvil;
luego, evalúas la expresión señalada (1*) para el punto B, cuya posición es: x = L, resuelves el último término, y queda:
vB2 = v02 - (4/3)*β*g*L3 (2),
que es la expresión del cuadrado de la velocidad del móvil en el punto B.
a)
Extraes raíz cuadrada positiva en ambos miembros de la ecuación señalada (2), y queda:
vB = √(v02 - (4/3)*β*g*L3),
que es la expresión de la velocidad del móvil en el punto B.
b)
Planteas la expresión del módulo de la acción normal que ejerce la pista circular en un punto genérico (es muy conveniente que hagas un esquema de fuerzas, y observa que indicamos con θ al ángulo que forma la vertical con el radio en el punto en estudio), y queda:
N(θ) = M*g*cosθ;
luego, planteas la expresión de la fuerza de rozamiento, y queda:
fr(θ) = -β*R2*M*g*cosθ,
y observa que tienes que la fuerza de rozamiento no es constante, y depende del ángulo θ;
luego, planteas la expresión del trabajo de la fuerza de rozamiento (observa que consideramos: θ = -π/2 para el punto B, y θ = π/2 para el punto más a la derecha de la pista semicircular), y queda:
Wfr = -π/2∫π/2 fr(θ)*dθ, sustituyes la expresión de la fuerza de rozamiento, extraes factores constantes, y queda:
Wfr = -β*R2*M*g*-π/2∫π/2 cosθ*dθ = -β*R2*M*g*[ senθ ] = evalúas = -β*R2*M*g*(1 - (-1)) = -2*β*R2*M*g (3).
Luego, planteas las expresiones de la energía potencial y de la energía cinética en el punto más alto de la pista circular, y queda:
EP1 = M*g*2*R = 2*M*g*R,
EC1 = (1/2)*M*v12;
y la expresión de la energía mecánica en el punto más alto queda:
EM1 = EP1 + EC1 = 2*M*g*R + (1/2)*M*v12 (4).
Luego, planteas la expresión de a energía mecánica en el punto B (observa que consideramos que su altura es igual a cero, por lo que su energía potencial también es igual a cero), y queda:
EMB = ECB = (1/2)*M*vB2, sustituyes la expresión señalada (2), y queda:
EMB = (1/2)*M*(v02 - (4/3)*β*g*L3) (5),
Luego, planteas la ecuación energía-trabajo entre el punto B y el punto más alto de la trayectoria semicircular, y queda:
EM1 - EMB = Wfr,
sustituyes las expresiones señaladas (4) (5) (3), y queda:
2*M*g*R + (1/2)*M*v12 - (1/2)*M*(v02 - (4/3)*β*g*L3) = -2*β*R2*M*g,
multiplicas por 2/M en todos los términos, y queda:
4*g*R + v12 - (v02 - (4/3)*β*g*L3) = -4*β*R2*g,
distribuyes el signo en el tercer término, y queda:
4*g*R + v12 - v02 + (4/3)*β*g*L3 = -4*β*R2*g,
multiplicas por 3en todos los términos, y queda:
12*g*R + 3*v12 - 3*v02 + 4*β*g*L3 = -12*β*R2*g (6).
Luego, planteas la condición crítica: la acción normal de la pista circular en el punto más alto es igual a cero, por lo que tienes que la única fuerza que actúa sobre el cuerpo es su peso, aplicas la Segunda Ley de Newton, y queda:
M*g = M*acp, y de aquí despejas:
acp = g, sustituyes la expresión de la aceleración centrípeta en función de la velocidad lineal, y queda:
v12/R = g, multiplicas por R en ambos miembros, y queda:
v12 = g*R (7).
Luego, sustituyes la expresión señalada (7) en el segundo término de la ecuación señalada (6), y queda:
12*g*R + 3*g*R - 3*v02 + 4*β*g*L3 = -12*β*R2*g,
reduces términos semejantes, y queda:
15*g*R - 3*v02 + 4*β*g*L3 = -12*β*R2*g,
restas 15*g*R y restas 4*β*g*L3 en ambos miembros, y queda:
-3*v02 = -12*β*R2*g - 15*g*R - 4*β*g*L3,
divides por -3 en todos los términos de la ecuación, y queda:
v02 = 4*β*R2*g + 5*g*R + (4/3)*β*g*L3,
extraes raíz cuadrada positiva en ambos miembros, y queda:
v0 = √(4*β*R2*g + 5*g*R + (4/3)*β*g*L3),
que es la expresión de la velocidad inicial mínima para que el móvil pueda recorrer la trayectoria circular, en función de los datos que tienes en tu enunciado.
Espero haberte ayudado.
-
BUENAS!! AGRADECERIA EL PLANTEAMIENTO DE ESTE PROBLEMA. LO HE INTENTADO MIL VECES PERO AL RESOLVERLO, ME DA EL TIEMPO=0 PORFAVOR AYUDENME PRONTO MUCHAS GRACIAS DE ANTEMANO
¿Cuánto tiempo tardará un móvil en alcanzar la velocidad de 80 km / h si parte del reposo y tiene una aceleración de 0,5 m / s2? Realiza el cálculo y escribe todas las ecuaciones correspondientes al movimiento del móvil mencionado.
-
Hola! Me podriais decir las formulas para el espacio recorrido y el desplazamiento en un gráfico
posición- tiempo de un MRU???
-
Buenas! Me podriais ayudar con este problema por favor?
Un coche circula a una velocidad de 60 km / h durante 1 hora y 15 minutos. Después se detiene durante 5 minutos y luego vuelve punto de partida a una Velocidad de 10 m / s durant 45 minutos. encuentra:
a) La Posición final.
b) El espacio total recorrido.
c) la velocidad media.
NO NECESITO LA SOLUCION PORQUE QUIERO HACERLO POR MI MISMA, PERO SI QUE AGRADECERIA UN POCO DE AYUDA EN CUANTO AL PLANTEAMIENTO. DE MOMENTO HE HECHO EL DIBUJO PERO AUN ASI NO ME ACLARO. MUCHAS GRACIA Y ESPERO PORFAVOR QUE ME AYUDEN ( ME ACONSEJAN HACERME PRO PARA PROFUNDIZAR MAS EN LOS CONOCIMIENTOS??)
ANTONIO MONTERO
el 2/1/19Tienes que plantear el problema por partes.
la primera parte (yo lo llamaré primer trayecto) el coche circula a 60km/h q lo pasamos a metros por segundo para que todo esté en las mismas magnitudes.
y está a esa velocidad durante una hora y cuarto o 4500s gracias a la fórmula de MRU sabemos que distancia es tiempo*velocidad entonces sacas los metros del primer trayecto.
el segundo trayecto es mas facil ya que está 5m o 300s pero como está parado la velocidad es 0, al sacar la distancia multiplicas por 0 y eso es 0 XD.
el tercer trayecto tienes q tener en cuenta que lo hace en dirección opuesta, lo haces igual q el primero está andando 45m o 2700s y va a 10m/s y sacas la distancia.
el apartado A te pregunta la posición final, pero tienes q tener en cuenta de q es en relación al punto de salida (bastante lógico la vd) pues restas el primer trayecto con el tercero, ya q el segundo no se movió.
el partado B te pregunta el espacio total recorrido, lo cual el la suma de todo lo q ha recorrido el coshe.
El apartado C es la velocidad media de todo el trayecto. Sabemos que velocidad es espacio / tiempo pues la velocidad media sale de dividir todo el espacio recorrido entre todo el tiempo que ha pasado.
Te dejo una foto de el ejer resuelto :)