-
Me dicen que una partícular de 1,5x10∧-8kg con una carga q= -3,64mC se mueve con una velocidad V=(2,75x10∧6i)ms∧-1 dentro de un campo magnético de valor B=(0,20i+0,20j)T
Me piden que calcule el radio y el paso de rosca de la trayectoria de la partícula.
Nota: No entiendo muy bien los valores de B.
Gracias.
Jerónimo
el 22/12/18Te dan la v y el campo B en notación vectorial, tienes que utilizar determinantes para calcular el producto vectorial (vxB)
Recuerda que F=q(vxB)
i j k
vxB= vi vj vk
Bi Bj Bk
-
a)
POR FAVOR ME PODÉIS AYUDAR CON ESTO Recuerde las características de las
asociaciones de resistencias en serie y en paralelo y razone si es posible
identificar alguna asociación de resistencias que permita simplificar la
resolución del circuito. Si es así, dibuje de nuevo el diagrama del circuito sustituyendo
el grupo de resistencias identificado por su resistencia equivalente. Calcule su
valor.
b) Utilizando las reglas de Kirchhoff, plantee
el sistema de ecuaciones necesario para resolver el circuito, calcule las
intensidades de corriente en todas las ramas y preséntelas, junto con
sus sentidos, en un diagrama. Si ha conseguido responder al apartado b la resolución se simplifica
notablemente.
c) Calcule las siguientes diferencias de
potencial: Vad = Va−Vd, Vba= Vb−Va
y Vec = Ve−Vc.
d) A la vista de los resultados
obtenidos, razone qué baterías entregan energía al circuito y cuáles la
consumen (si hubiera alguna en esta situación).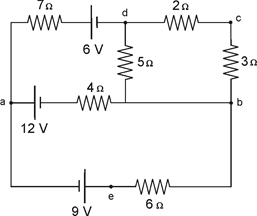
Raúl RC
el 21/12/18Hola, lamento no poder ayudarte con un ejercicio tan largo y propio de física de universidad.
Decirte que como excepción el profe grabó un vídeo sobre este tema que te ruego lo veas detenidamente, seguro que a partir de él sacas tus soluciones, nos cuentas.
Un saludo.
Leyes de KirchhoffAlguien
el 23/12/18Para el apartado
a) Simplemente es sumar la resistencia de 2 con la de 3, quedandose una de 5, ya que están en serie.
b) Aplicas las leyes de Kirchhoff, y te saldrá un sistema de 3 ecuaciones con 3 incógnitas.
c) Con las intensidades ya halladas es aislar esa parte del circuito e ir calculando las caídas de tensión
Antonio Silvio Palmitano
el 26/12/18Vamos con una orientación.
En un circuito como el que tienes en tu figura, es más conveniente plantear de salida las Leyes de Kirchhoff para resolverlo.
Ahí vamos.
Observa que hemos supuesto los sentidos de las corrientes, a fin de plantear el problema.
Luego, observa que tienes cuatro nudos, por lo que elegimos a tres de ellos: a, b, f, y quedan las ecuaciones:
(Ientrantes = Isalientes):
I1 + I3 = I2,
I2 = I7 + I45,
I7 = I1 + I6,
y como no tienes resistencia entre los extremos de la rama correspondiente a la corriente señalada I7, tienes que su valor es igual a cero, por lo que reemplazas y las tres ecuaciones quedan:
I1 + I3 = I2, de aquí despejas: I3 = -I1 + I2 (1),
I2 = I45, de aquí despejas: I45 = I2 (2),
0 = I1 + I6, de aquí despejas: I6 = -I1 (3).
Luego, consideras la malla gris (consideramos positivo el sentido antihorario), y queda:
(R4 + R5)*I45 - R6*I6 = 0,
reemplazas los valores de las resistencias, resuelves coeficientes, y queda:
5*I45 - 5*I6 = 0,
divides por 5 en todos los términos de la ecuación, y queda:
I45 - I6 = 0,
sustituyes las expresiones señaladas (3) (2), y queda:
I2 - (-I1) = 0, de aquí despejas: I2 = -I1 (4).
Luego, consideras la malla rosa (consideramos positivo el sentido antihorario), y queda:
R1*I1 + R2*I2 + 0*R7 = ε1 + ε2,
cancelas el término nulo, reemplazas los valores de las resistencias, reemplazas los valores de las fuerzas electromotrices, resuelves términos, y queda:
4*I1 + 6*I2 = 21,
sustituyes la expresión señalada (4), resuelves el segundo término, y queda:
4*I1 - 6*I1 = 21,
resuelves el primer miembro, divides en ambos miembros por -2, y queda:
I1 = -10,5 A (observa que esta corriente tiene sentido contrario al que hemos supuesto),
luego, reemplazas en las ecuaciones señaladas (4) (3), y queda:
I2 = 10,5 A,
I6 = 10,5 A;
luego, reemplazas los valores remarcados en las ecuaciones señaladas (1) (2), resuelves, y queda:
I3 = 21 A,
I45 = 10,5 A.
-
Por favor me podéis ayudar con este ejercicio de campo magnético:
Un electrón se mueve en el eje X a 150ms∧-1, y otro se mueve en el eje Y a 300ms∧-1. En cierto instante, el primer electrón se encuentra en P(1,0,0) y el segundo en Q(0,-1,0), con las distancias expresadas en metros.
1.- Calcula el campo magnético creado por los electrones en los puntos A(2,0,0) y B(0,0,2).
2.- ¿Qué fuerza magnética ejerce el primer electrón sobre el segundo?
Gracias
Raúl RC
el 24/12/18Vamos con una orientacion:
a) Para calcular el campo magnetico creado por una carga puntual en movimiento debes aplicar la expresion:
B=(μ0·q/4π)·(v x ur)/r2 donde ur es el vector unitario que indica la trayectoria que sigue el electrón, siendo r=AP=((1,0,0)-(2,0,0)=(-1,0,0) m cuyo módulo será ΙrΙ=1 m
Lo siguiente de la fórmula es calcular el producto vectorial forma por el vector velocidad y el unitario.
Un vez lo tengas para ambos electrones en el punto A lo siguiente es aplicar superposición y sumar los campos creados por ambos electrones en el punto A y B respectivamente
b) Este apartado es un poco mas largo y complejo de explicar por aqui, en el siguiente link verás las expresiones que debes utilizar, espero te sirvan http://laplace.us.es/wiki/index.php/Fuerza_magn%C3%A9tica_entre_dos_cargas_puntuales
Felices fiestas ;)
-
Hola únicos. No sé cómo hacer este ejercicio "Descomponer un vector v dirigido según la dirección i-j+k y módulo √(27) según las direcciones de los vectores a= i+j; b= j+2k; c= 2i+k ."
Antonio Silvio Palmitano
el 21/12/18Tienes la expresión de un vector (v)que es múltiplo del vector d = < 1 , -1 , 1>, cuyo módulo es:
|v| = √(27) (1),
por lo que puedes plantear la ecuación vectorial:
v = k*d, con k ∈ R, k > 0, aquí sustituyes la expresión del vector d, y queda:
v = k*< 1 , -1 , 1>, aquí resuelves el producto en el segundo miembro, y queda:
v = < k , -k , k > (2), cuyo módulo queda expresado:
|v| = √(3)*k (3);
luego, igualas las expresiones señaladas (3) (1), y queda:
√(3)*k = √(27), aquí divides por √(3) en ambos miembros, resuelves, y queda: k = 3;
luego, reemplazas este valor en la expresión del vector señalada (2), y queda:
v = < 3 , -3 , 3 > (4).
Luego, tienes los vectores que determinan las direcciones de proyección, de los cuáles indicamos sus módulos:
a = < 1 , 1 , 0 >,
b = < 0 , 1 , 2 >,
c = < 2 , 0 , 1 >.
Luego, planteas la expresión del vector v como combinación lineal de los vectores a, b y c, y queda:
k*a + m*b + n*c = v (5),
con k, m y n pertenecientes a R;
luego, sustituyes las expresiones de los vectores, y queda:
k*< 1 , 1 , 0 > + m*< 0 , 1 , 2 > + n*< 2 , 0 , 1 > = < 3 , -3 , 3 > (*),
resuelves los productos en los términos y luego la suma vectorial en el primer miembro, y queda:
< k+2n , k+m , 2m+n > = < 3 , -3 , 3 >;
luego, por igualdad entre expresiones vectoriales, igualas componente a componente, y queda:
k + 2n = 3 (6),
k + m = -3, aquí restas m en ambos miembros, y queda: k = -3-m (7),
2m + n = 3, aquí restas 2m en ambos miembros, y queda: n = 3-2m (8);
luego, sustituyes la expresiones señaladas (7) (8) en la ecuación señalada (6), y queda:
-3 - m + 2(3 - 2m) = 3, distribuyes y reduces términos semejantes en el primer miembro, y queda:
3 - 5m = 3, y de aquí despejas: m = 0;
luego, reemplazas el valor remarcado en las expresiones señaladas (7) (8), resuelves, y queda: k = -3 y n = 3.
Luego, reemplazas los valores remarcados en la ecuación vectorial señalada (*), y queda:
-3*< 1 , 1 , 0 > + 0*< 0 , 1 , 2 > + 3*< 2 , 0 , 1 > = < 3 , -3 , 3 >;
luego, sustituyes las expresiones de los vectores, y queda:
-3*a + 0*b + 3*c = v.
Espero haberte ayudado.
Jerónimo
el 21/12/18Primero calculas Uv (vector unitario en la dirección v Uv= (i-j+k)/√3 Como tiene que tener de módulo √27, quedaría √27 (i-j+k)/√3 = 3i-3j+3k.
A continuación calculas los vectores unitarios de las tres direcciones y hallas su producto escalar con el vector v y ya lo tienes.
Ua=i+j/√2 Ub=j+2k/√5 Uc=2i+k/√5
proyecciones : (producto escalar)
(3i-3j+3k) (i+j/√2) = 0
(3i-3j+3k) (j+2k/√5 = 3/√5
(3i-3j+3k) (2i+k/√5) = 9/√5
-
hola, tengo dudas sobre este ejercicio de movimiento armónico simple, ya que creo que le faltan datos. he intentado de resolverlo pero no me sale, si alguien podría resolverlo me seria de gran ayuda, gracias.
Un cuerpo de 92 g de masa está enganchado a un muelle y experimenta un movimiento armónico simple, por lo que en el instante inicial elongación es la sexta parte de la amplitud, mientras que la velocidad y la aceleración son, respectivamente, -0,38 m / s y 5,42 m / s2 a) Escribir las ecuaciones del movimiento, de la velocidad y de la aceleración.
Antonio Silvio Palmitano
el 21/12/18Puedes comenzar por plantear las expresiones de la elongación, la velocidad y la aceleración del oscilador en función del tiempo:
x(t) = A*cos(ω*t+φ) (1),
v(t) = -ω*A*sen(ω*t+φ) (2),
a(t) = -ω2*A*cos(ω*t+φ) (3).
Luego, tienes los datos iniciales (recuerda que la aceleración siempre tiene sentido opuesto a la elongación):
x(0) = -(1/6)*A,
v(0) = -0,38 m/s,
a(0) = 5,42 m/s2;
luego, sustituyes las expresiones señaladas (1) (2) (3) evaluadas en los primeros miembros, cancelas términos nulos en los argumentos de las expresiones trigonométricas, y queda:
A*cos(φ) = -(1/6)*A (1*),
-ω*A*sen(φ) = -0,38 (2*),
-ω2*A*cos(φ) = 5,42 (3*);
luego, divides por A en ambos miembros de la ecuación señalada (1*), y queda:
cos(φ) = -1/6, aquí compones en ambos miembros con la función inversa del coseno, y queda:
φ ≅ 1,738 rad, que es el valor de la fase inicial;
luego, sustituyes el valor remarcado en las ecuaciones señaladas (2*) (3*), resuelves los valores de las expresiones trigonométricas, y queda:
-ω*A*0,986 ≅ -0,38, aquí divides por -0,986 en ambos miembros, y queda: ω*A ≅ 0,385 m/s (4),
-ω2*A*(-1/6) = 5,42, resuelves signos, multiplicas por 6 en ambos miembros, y queda: ω2*A ≅ 32,52 m/s2 (5);
luego, divides miembro a miembro la ecuación señalada (5) entre la ecuación señalada (4), resuelves el segundo miembro, y queda:
ω ≅ 84,468 rad/s, que es el valor de la pulsación;
luego, reemplazas este último valor remarcado en la ecuación señalada (4), y queda:
84,468*A ≅ 0,385, aquí divides por 84,468 en ambos miembros, y queda:
A ≅ 0,005 m, que es el valor de la amplitud de elongación.
Luego, reemplazas los valores remarcados en las ecuaciones señaladas (1) (2) (3), resuelves coeficientes, y queda:
x(t) = 0,005*cos(84,468*t+1,738), que es la expresión de la función elongación,
v(t) = -0,422*sen(84,468*t+1,738), que es la expresión de la función velocidad,
a(t) = 35,674*cos(84,468*t+1,738), que es la expresión de la función aceleración;
y observa que por las aproximaciones que hemos realizado tienes discrepancias menores cuando evalúas estas expresiones para el instante inicial t = 0, con respecto a los valores iniciales que tienes en tu enunciado.
Espero haberte ayudado.
-
Por favor me podéis ayudar con este ejercicio de campos:
Si tenemos una carga puntual que entra en una región R con un velocidad de 120ms∧-1 a lo largo del eje Z. En esa región hay un campo magnético de 0,25T a lo largo del eje X y un campo eléctrico desconocido.
Determinar dicho campo para que la carga tenga en R un movimiento rectilíneo uniforme.
Muchas gracias.
Jerónimo
el 20/12/18Para que el movimiento sea uniforme v=cte a=0 ∑F=0 Fmagnética=Feléctrica
Fmagnética= q(vxB)=qvBsen90º=qvB . El vector velocidad (OZ) forma con el vector campo magnético B (OX) un ángulo de 90º y produce siguiendo la regla del sacacorchos (de v a B) una fuerza magnética perpendicular a ambos vectores y con sentido positivo del eje y . Para equilibrar esa fuerza, hay que aplicar una F eléctrica con dirección OY y sentido negativo (suponemos que la q puntual es de signo positivo).
qvB=qE E=vB=120 x0,25=30 N/C
-
Antonio Silvio Palmitano
el 20/12/18Vamos con una orientación.
Considera un sistema de referencia con eje OX paralelo al plano inclinado con sentido positivo hacia arriba, con eje OY perpendicular al plano inclinado con sentido positivo hacia arriba, con origen de coordenadas en el pie del plano inclinado, y con instante inicial: ti= 0 correspondiente al inicio del ascenso del cuerpo.
Luego, observa que sobre el cuerpo actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical hacia abajo;
Acción normal del plano inclinado: N, perpendicular al plano inclinado, hacia arriba;
Rozamiento dinámico: fr = μ*N, paralela al plano y opuesto al desplazamiento del cuerpo.
Luego, tienes dos etapas (ascenso y descenso), para las que aplicas la Segunda Ley de Newton, y tienes:
1)
Ascenso:
-M*g*cos(45°) - μ*N = M*a1,
N - M*g*cos(45°) = 0, aquí despejas: N = M*g*cos(45°);
luego, sustituyes en la primera ecuación, y queda:
-M*g*cos(45°) - μ*M*g*cos(45°) = M*a1, divides por M en todos los términos, y queda:
-g*cos(45°) - μ*g*cos(45°) = a1, reemplazas los valores de las razones trigonométricas, y queda:
-g*( 1/√(2) ) - μ*g*( 1/√(2) ) = a1, extraes factores comunes, y queda
-( 1/√(2) )*g*(1 + μ) = a1 (1),
que es la expresión de la aceleración del cuerpo en la etapa de ascenso;
luego, planteas las ecuaciones tiempo-posición y tiempo-velocidad de Movimiento Rectilíneo Uniformemente Variado (observa que la posición inicial es: xi = 0, y que indicamos con L a la distancia recorrida), y queda:
x = vi*t + (1/2)*a1*t2,
v = vi + a1*t;
luego, sustituyes los datos finales para esta etapa (x = L, v = 0), y queda:
L = vi*t1 + (1/2)*a1*t12 (2),
0 = vi + a1*t1 (3).
2)
Descenso (consideramos instante inicial ti = 0 cuando el cuerpo comienza a descender, y presta atención al sentido de la fuerza de rozamiento):
-M*g*cos(45°) + μ*N = M*a2,
N - M*g*cos(45°) = 0, aquí despejas: N = M*g*cos(45°);
luego, sustituyes en la primera ecuación, y queda:
-M*g*cos(45°) + μ*M*g*cos(45°) = M*a2, divides por M en todos los términos, y queda:
-g*cos(45°) + μ*g*cos(45°) = a2, reemplazas los valores de las razones trigonométricas, y queda:
-g*( 1/√(2) ) + μ*g*( 1/√(2) ) = a2, extraes factores comunes, y queda
-( 1/√(2) )*g*(1 - μ) = a2 (4),
que es la expresión de la aceleración del cuerpo en la etapa de descenso;
luego, planteas las ecuaciones tiempo-posición y tiempo-velocidad de Movimiento Rectilíneo Uniformemente Variado (observa que la posición inicial es: xi = L, y que la velocidad inicial es: vi = 0), y queda:
x = L + (1/2)*a2*t2,
v = a2*t;
luego, sustituyes los datos finales para esta etapa (x = 0, v = vf a determinar), y queda:
0 = L + (1/2)*a2*t22 (5),
vf = vi + a2*t2 (6).
Luego, tienes la relación entre los intervalos de ascenso y de descenso en tu enunciado, por lo que puedes plantear la ecuación:
t2 = 2*t1 (7).
Luego, sustituyes la expresión señalada (7) en las ecuaciones señaladas (5) (6), resuelves términos, y queda:
0 = L + 2*a2*t12 (5*),
vf = vi + 2*a2*t1 (6*).
Luego, con las ecuaciones señaladas (1) (2) (3) (4) (5*) (6*) tienes el sistema:
a1 = -( 1/√(2) )*g*(1 + μ) = a1 (1),
L = vi*t1 + (1/2)*a1*t12 (2),
0 = vi + a1*t1 (3),
a2 = -( 1/√(2) )*g*(1 - μ) (4),
0 = L + 2*a2*t12 (5*),
vf = vi + 2*a2*t1 (6*).
Luego, puedes sustituir la expresión señalada (2) en la ecuación señalada (5*),
y luego las expresiones señaladas (1) (4) en las demás ecuaciones,
y tendrás un sistema de tres ecuaciones con tres incógnitas: vi, vf y μ.
Te dejo la tarea de resolver este problema (más bien, problemón),
y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
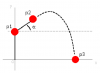
Hola, me han puesto el siguiente ejercicio en la universidad y ando pillado.
Se pide encontrar la ecuación que nos permita hallar el angulo (α) de salida de un proyectil desde (p2) sabiendo:
- La magnitud de su velocidad inicial (v)
- Las coordenadas del punto de llegada (p3) que se halla en el origen de ordenadas: (p3y) = 0
- Las coordenadas de un punto fijo (p1) con el que (p2) se relaciona directamente, (p1) se halla en el origen de abscisas: (p1x) = 0
- La distancia de (p1) a (p2)
Además se proporcionan la siguiente información:
- La gravedad es de -9.8m/s, es decir, hacia abajo en Y
- No existe rozamiento de ningún tipo
- Dirección inicial del proyectil = (p2 - p1) (de p1 a p2)
- El punto de salida (p2) pivota sobre otro punto conocido (p1) a una distancia (d) constante
- Siendo (p2x) la componente X de (p2), (p1x) la componente X de (p1): p2x = p1x + cos(α) * d
- Siendo (p2y) la componente Y de (p2), (p1y) la componente Y de (p1): p2y = p1y + sin(α) * d.
Muchas gracias!
Raúl RC
el 21/12/18Por lo que veo estas ante un ejercicio de tiro parabólico.
Lamentablemente el nivel que tocamos no va mas allá del propio de secundaria y bachiller, pero estoy convencido que esta serie de vídeos que grabó el profe sobre esta temática te ayudarán con tu planteamiento y posterior resolución, nos cuentas ok?
Tiro oblicuo o parabólico -