-
Hola estoy haciendo una guía de física y esta es la última duda que tengo
El movimiento vertical de una masa unida a un resorte se expresa mediante la relación x = 10sin2t+15cos2t+100 , donde x y t se expresan en mm y s, respectivamente. Calcular la velocidad máxima que alcanza la partícula
Lo que he hecho
Se me ocurre derivar la posición para obtener la velocidad quedando v(t) = 20cos(2t)-30sin(2t) pero luego no se me ocurre que mas hacer
De antemano gracias
Fernando Alfaro
el 8/10/18Es que los "grados" en realidad es el tiempo.
Vmax ocurre en t = 151.85
v(t) = 20cos(2t)-30sin(2t) => v(151.85) = 20cos(2*151.85) - 30sin(2*151.85) = 36.06
Y ahora que lo veo me dan dudas de si esos últimos pasos son correctos y t está en segundos.
Habría que saber si la constante ω dentro de sin y cos está en rad/s o en °/s.
Me excede el darme cuenta a la ligera si ese detalle afecta o no al resultado final.
-
Hola tengo una duda en este ejercicio
El movimiento de una partícula esta descrito por x(t) =2t3-15t2+24t+4 , donde x y t se expresan en metros y segundos, respectivamente
a) En que instante la velocidad es cero?
b) La distancia total recorrida hasta el momento en que la aceleración es cero
Lo que he hecho
a) Basta derivar e igualar a cero quedando v(t) = 6t2-15t+24 → 6t2-15t +24= 0 . Por lo tanto t = 1.25
b) Lo que hice fue derivar la velocidad quedando a(t) = 12t -15. Luego igualando a 0 → 12t-15 = 0 → t= 1.25.
Mi duda ¿la distancia total recorrida seria calcular la integral definida desde 0 hasta 1.25 de la función 12t-15 ?
Fernando Alfaro
el 7/10/18En a) hay un error en la derivada. Faltó bajar el 2 multiplicando.
v(t) = 6t² - 30t + 24 = 0 => t=1 s y t=4 s
b) Corrigiendo el error anterior, a(t) = 12t - 30 = 0 => t= 2.5 s
Respecto a tu duda, la respuesta es: mas o menos. La integral definida de 12t -30 seguro que no. Deberías integrar 2 veces la aceleración para obtener la posición, y determinar las constantes de integración. Eso da como resultado la función de posición x(t) que ya la tienes. Lo que debes hacer es sustituir en x(t) el valor de t en donde a(t) = 0.
x(2.5) = 2*(2.5)³ - 15*(2.5)² + 24*(2.5) + 4 = 31.25 - 93.75 + 60 + 4 = 1.5 m
fabian
el 7/10/18Fernando Alfaro
el 7/10/18"¿no estaríamos encontrando la posición a los 2.5 segundos?". Totalmente. Posición y desplazamiento dan lo mismo si se mide el desplazamiento desde el origen.
Pero ahora caigo con que pregunta por el recorrido y no por el desplazamiento. Perdón por el error.
Encuentro algunas ambiguedades en el termino recorrido.
Me baso en esta definición de recorrido: El espacio recorrido por una partícula en un intervalo de tiempo determinado es la longitud de la trayectoria que ha descrito.
Debes tener en cuenta el momento en que la velocidad de la partícula cambia de signo y en vez de alejarse del origen, se acerca. Calcular ambos desplazamientos por separado y sumarlos en valor absoluto.
El signo de la velocidad es + entre 0s y 1s, en ese intervalo la partícula se aleja del origen. Su desplazamiento en dicho intervalo es:
Δx1 = (x(1) - x(0)) = (2*(1)3-15*(1)2+24*(1) + 4) - (2*(0)3-15*(0)2+24*(0)+4) = (2 - 15 + 24 + 4) - (4) = 11m.
Notas la similitud con una integral definida? Es la integral definida de la velocidad entre 0 y 1
Cuando la partícula llega a t =1s su velocidad es 0, la partícula se detiene y como la velocidad cambia de signo, comienza a moverse hacia el origen.
El signo de la velocidad es - entre 1s y 4s, por lo tanto es - entre 1s y 2.5s. El desplazamiento en ese intervalo de tiempo es:
Δx2 = (x(2.5) - x(1)) = (2*(2.5)³ - 15*(2.5)² + 24*(2.5) + 4) - (2*(1)3-15*(1)2+24*(1) + 4) = 1.5 - 15 = - 13.5m
Luego el recorrido total es |Δx1| + |Δx2| = 11 + 13.5 = 24.5 m
-
Hola tengo dudas con este ejercicio
Un reptil camina en linea recta sobre el eje x con la dirección positiva hacia la derecha. La ecuación de la posición de la tortuga en función del tiempo es:
x(t) = 50 cm + (2 cm/s)t -(0.0625 cm/s2) t 2
a) Determine velocidad inicial, posición inicial y aceleración inicial del reptil
b) En que instante el reptil tiene velocidad cero?
c) Cuanto tiempo después de ponerse en marcha el reptil regresa al punto de partida
d)En que instantes el reptil esta a una distancia de 10 cm de su punto de partida
e) Que velocidad (magnitud y dirección) tiene el reptilen cada uno de esos instantes?
Lo que he hecho
a) Para obtener la posición inicial basta reemplazar t=0 en x(t) quedando 50 cm la posición inicial. Por otro lado para obtener la velocidad inicial debemos derivar x(t) y reemplazar en t= 0 resultando v(t) =2 + 0.125 t , reemplzando t=0 resulta v (inicial) = 2 cm/s. La aleración basta derivar la velocidad resultando a= 0.125 cm/s2
Los otros apartados no se me ocurre que hacer
De antemano muchas gracias
Antonio Silvio Palmitano
el 7/10/18a)
Observa que la aceleración es: a = -0.125 cm/s2.
b)
Planteas la expresión de la función velocidad de Movimiento Rectilíneo Uniformemente Acelerado, reemplazas los valores de la velocidad inicial y de la aceleración, y queda:
v(t) = 2 - 0.125*t;
luego, planteas la condición de velocidad nula (v(t) = 0), y tienes la ecuación:
2 - 0.125t = 0, resuelves esta ecuación, y queda:
t = 16 s.
c)
Planteas la condición de posición inicial (x(t) = 50 cm), y tienes la ecuación:
50 + 2t - 0.0625t2 = 50, restas 50 en ambos miembros, y queda:
2t - 0.0625t2 = 0, extraes factor común, y queda:
t*(2 - 0.0625t) = 0; luego, por anulación de una multiplicación, tienes dos opciones:
t = 0, que es el instante inicial,
2 - 0,0625t = 0, de donde puedes despejar:
t = 32 s, que es el instante en que el reptil alcanza nuevamente su posición inicial.
d)
Planteas la condición para la posición indicada, y tienes la ecuación:
50 + 2t - 0.0625t2 = 10, restas 10 en ambos miembros, ordenas términos, y queda:
-0.0625t2 + 2t + 40 = 0, que es una ecuación polinómica cuadrática, que puedes resolver y considerar su solución positiva.
e)
Solo tienes que evaluar la expresión de la función velocidad en los instantes indicados.
Espero haberte ayudado.
fabian
el 7/10/18Muy claro muchas gracias. En el apartado e me complica calcular la velocidad ya que es un vector y no sabría como calcular su magnitud y dirección. Por lo que entendi debo evaluar por ejemplo en el instante en que tiene velocidad cero que corresponde a los 16 segundos en la función v(t) = 2-0.125t resultando v(16) = 2 - 0.125 (16) = 0 (obviamente 0) pero como calculo la magnitud y dirección
Fernando Alfaro
el 7/10/18En un movimiento rectilíneo, el sentido de los vectores esta dado por el signo.
"dirección positiva hacia la derecha". Establecido el marco de referencia, en este caso los valores que resulten con signo positivo estarán direccionados hacia la derecha, y los valores que resulten negativos direccionados hacia la izquierda.
En cuanto a la magnitud (o el modulo) tienes que calcular el valor numérico de v en los instantes indicados.
En el caso en que v = 0, la magnitud del vector es 0 y un vector de magnitud 0 no tiene dirección.
Mas claro ahora?
Fernando Alfaro
el 8/10/18Corrijo un detalle del apartado d) y voy con las respuestas concretas de e) a ver si logro despejarte toda duda en esto de modulo y dirección de vectores en una dimensión.
En el apartado d) Antonio iguala la ec de posición a 10, pero eso da como resultado el tiempo que demora en llegar a 10 cm de el origen y la pregunta es tiempos a 10cm del punto de partida. Su punto de partida no es el origen, es 50cm del origen. por lo tanto hay que igualar la ec de posición a 40cm y a 60cm
x(t) = 50 + 2t - 0.0625t2 = 60 => -10 + 2t - 0.0625t² = 0 => t = 6.2s y t = 25.8s
x(t) = 50 + 2t - 0.0625t2 = 40 => 10 + 2t - 0.0625t² = 0 => t = 36.4s
Apartado e) Cuando se trabaja con vectores que pertenecen todos a la misma recta, como es el caso de un movimiento rectilíneo, signos opuestos indican vectores de sentidos opuestos. Cuando se establece un convenio, por ejemplo "dirección positiva hacia la derecha", lo dicho en la respuesta anterior.
Ahora, v(t) = 2 - 0.125*t. Determinar modulo y dirección de v en: t =16 s, t =32 s, t =6.2s, t =25.8s y t =36.4s
Me salteo la aritmética.
v(16) = 0 => Modulo: 0 Dirección: no tiene dirección. v(32) = -2 = > Modulo: 2 Dirección: hacia la izquierda.
v(6.2) = 1.225 => Modulo: 1.225 Dirección: hacia la derecha. v(25.8) = -1.225 => Modulo: 1.225 Dirección, hacia la izquierda.
v(36.4) = -2.25 => Modulo 2.25 Dirección: hacia izquierda.
-
Hola buenas, quiero que alguien me ayude a argumentar y razonar un ejercicio:
El momento de Inercia de una particula es con respecto al eje elegido?. Y el de un sistema de particulas discreto?
Gracias.
Antonio Silvio Palmitano
el 7/10/18La respuesta a tu primera pregunta es Sí, y la expresión del momento de inercia de la partícula con respecto a un eje (O) tiene la expresión:
IO = M*r2 (observa que es la expresión de una magnitud escalar, y que su unidad de medida internacional es: Kg*m2),
donde M es la masa de la partícula, y r2 es la longitud del segmento de recta perpendicular al eje O, con extremos en el punto en el cuál está ubicada la masa y en el punto de intersección de dicha recta con el eje de giros.
Luego, para un sistema de partículas, tienes que el momento de inercia total es igual a la suma algebraica de los momentos de inercia individuales de las partículas.
Espero haberte ayudado.
-
Hola tengo dudas con este ejercicio
Una partícula se mueve a lo largo del eje x de acuerdo con la ecuación x(t) = 3t2 +2t + 3 m , donde t esta en segundos
Determine:
a. La rapidez promedio entre t=2s y t=3s
b. La rapidez instantánea en t=2s y t=3s
c. La aceleración promedio entre t=2 s y t= 3 s
d. La aceleración instantánea en t= 2 s y t= 3 s
Lo que he hecho:
b) Debemos derivar la posición para obtener la rapidez. v = 6t + 2 . Por lo tanto la rapidez en t = 2 es 14 m/s, y en t= 3 es 20 m/s
d) debemos derivar la rapidez para obtener la aceleración. a = 6 que seria el valor de la aceleración instantanea en todo momento por lo cual en t= 2 s y t= 3 s la aceleración es 6 m/s2
el a y el c no lo se hacer
De antemano muchas gracias
Fernando Alfaro
el 7/10/18Por rapidez promedio supongo que se refiere a rapidez media, y por aceleración promedio a aceleración media.
La velocidad media es: vm = Δx/Δt y la aceleración media: am = Δv/Δt
x(2) = 12 + 4 + 3 = 19 y x(3) = 27 + 6 + 3 = 19
vm = Δx/Δt = (36-19)/(3-2) = 17 m/s
Y de los datos que tu ya calculaste, am = Δv/Δt = (20-14)/(3-2) = 6 m/s². Como debe ser, ya que la aceleración es constante y en ese caso el valor medio y el instantáneo coinciden.
-
Necesito ayuda: La distancia entre los centros de dos masas M1 y M2 esféricas y homogéneas de
radios R1 y R2 respectivamente es de 30 R2. Determina la relación entre lasdensidades de las dos esferas sabiendo que el punto sobre el que ejercen la mismafuerza gravitatoria se encuentra en 20R2 de M1. Dato: R1 = 10 R2O1O2 se encuentra a 20R2 de O1. Dato: R1=10R2 -
David
el 10/10/18Calcula la energía potencial a 120 km de altura y a 300 km de altura. Y réstalas. Nada más.
Revisa estos vídeos.. Gravitación Universal
Te falta como dato el radio del planeta. Porque la altura es la suma de el radio del planeta más la altura... -
No logro averiguarlo. Gracias!
Un objeto realiza un movimiento circular de radio 9m partiendo del reposo al tiempo t = 0 s, con aceleración angular α = 1/3 rad / s ^ 2. El módulo de la aceleración total del objeto al tiempo t = 2 s vale:
SOL: 5 m / s ^ 2
Fernando Alfaro
el 7/10/18 -
- no soy capaz de razonarlo, espero que me podáis ayudar por favor
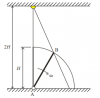
La figura representa una lámpara encendida, situada a una altura 2H sobre el suelo. La varilla AB de longitud H gira uniformemente con velocidad angular ω partiendo de la vertical. Hállese la velocidad de la sombra del extremo B de la varilla
a) cuando forma 45º con el suelo
b) cuando contacta con el suelo
Raúl RC
el 8/10/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
Antonio Silvio Palmitano
el 8/10/18Establece un sistema de referencia con origen de coordenadas en el punto A, eje OX horizontal con sentido positivo hacia la derecha según la imagen, con eje OY vertical con sentido positivo hacia arriba, y con instante inicial: ti = 0 correspondiente al momento en que la varilla se encuentra en posición vertical.
Luego, tienes los datos:
Longitud de la varilla: H,
Módulo del desplazamiento angular de la varilla con respecto al eje OY: ωt.
Luego, tienes que la expresión del punto genérico B en función del ángulo girado por la varilla es:
B( H*sen(ωt) , H*cos(ωt) ) (1).
Luego, tienes para la recta inclinada que pasa por el punto B que tienes en tu imagen:
Ordenada al origen: 2H,
y puedes designar:
Abscisa al origen: u,
y observa que u es la componente horizontal de la posición de la sombra que proyecta el extremo de la barra;
y, luego, planteas la ecuación cartesiana segmentaria para esta recta, y queda:
x / u + y / 2H = 1,
sustituyes las coordenadas del punto B, cuya expresión está señalada (1), y queda:
H*sen(ωt) / u + H*cos(ωt) / 2H = 1,
simplificas el segundo término, y queda:
H*sen(ωt) / u + cos(ωt) / 2 = 1,
restas cos(ωt) / 2 en ambos miembros, y queda:
H*sen(ωt) / u = 1 - cos(ωt) / 2,
extraes denominador común en el segundo miembro, y queda:
H*sen(ωt) / u = ( 2 - cos(ωt) ) / 2,
multiplicas por 2u en ambos miembros, y queda:
2H*sen(ωt) = u*( 2 - cos(ωt) ),
divides por ( 2 - cos(ωt) ) en ambos miembros, y queda
2H*sen(ωt) / ( 2 - cos(ωt) ) = u,
escribes esta ecuación tal como la lees de derecha a izquierda, y queda:
u = 2H*sen(ωt) / ( 2 - cos(ωt) ),
que es la expresión de la posición de la sombra del extremo de la varilla en función del tiempo;
luego, derivas con respecto al tiempo (observa que debes aplicar la regla de una división de funciones), y la velocidad queda expresada:
v = [ 2ωH*cos(ωt)*( 2 - cos(ωt) ) - 2ωH*sen(ωt)*sen(ωt) ] / ( 2 - cos(ωt) )2,
distribuyes el primer término en el numerador, reduces factores semejantes en el segundo término del numerador, y queda:
v = [ 4ωH*cos(ωt) - 2ωH*cos2(ωt) - 2ωH*sen2(ωt) ] / ( 2 - cos(ωt) )2,
extraes factor común en el numerador, y queda:
v = 2ωH*[ 2*cos(ωt) - cos2(ωt) - sen2(ωt) ] / ( 2 - cos(ωt) )2,
extraes factor común entre los dos últimos términos del agrupamiento del numerador, y queda:
v = 2ωH*[ 2*cos(ωt) - ( cos2(ωt) + sen2(ωt) ) ] / ( 2 - cos(ωt) )2,
aplicas la identidad trigonométrica fundamental (o pitagórica) en el segundo término del agrupamiento del numerador, y queda:
v = 2ωH*[ 2*cos(ωt) - 1 ] / ( 2 - cos(ωt) )2.
a)
Tienes el valor del desplazamiento angular: ωt = 45°, reemplazas este valor, y queda:
v = 2ωH*[ 2*cos(45°) - 1 ] / ( 2 - cos(45°) )2,
reemplazas los valores exactos de las expresiones trigonométricas, y queda:
v = 2ωH*[ 2*√(2)/2 - 1 ] / ( 2 - √(2)/2 )2,
simplificas en el primer término del agrupamiento del numerador, extraes denominador común y distribuyes la potencia en el denominador principal, y queda:
v = 2ωH*[ √(2) - 1 ] / ( 4 - √(2) )2/4,
resuelves la división principal, y queda:
v = 8ωH*[ √(2) - 1 ] / ( 4 - √(2) )2.
b)
Observa que tienes el valor del desplazamiento angular: ωt = 90°, reemplazas este valor, y queda:
v = 2ωH*[ 2*cos(90°) - 1 ] / ( 2 - cos(90°) )2,
reemplazas los valores exactos de las expresiones trigonométricas, y queda:
v = 2ωH*[ 2*0 - 1 ] / ( 2 - 0 )2,
resuelves y cancelas términos nulos, y queda:
v = 2ωH*[ -1 ] / ( 2 )2,
resuelves, simplificas, y queda:
v = -ωH/2.
Espero haberte ayudado.
-
Tengo problemas con este ejercicio
Se han colocado dos cargas de 1µC y -9µC en (0,0) y en (3,0) respectivamente :
a. Calcule el punto donde el vector campo es nulo
b. Calcule el vector campo en (4,2)
c. Que fuerza actuaria sobre una carga de 2µC situada en ese punto
d. Calcule el trabajo para trasladar esa carga hasta (3,4)