-
Antonio Silvio Palmitano
el 29/8/18Planteas la condición de equilibrio en las bases de los tubos verticales, y queda:
pA = δ*g*L,
pa = δ*g*(L-h);
luego, restas miembro a miembro entre ambas ecuaciones, y queda:
pA - pa = δ*g*L - δ*g*(L-h), distribuyes el último término, cancelas términos opuestos, y queda:
pA - pa = δ*g*h (1).
Planteas la ecuación de caudal, y queda:
A*vA = a*va, sustituyes la expresión del área menor en función del área mayor que tienes en tu enunciado, y queda:
A*vA = 0,22*A*va, divides por A en ambos miembros, y queda:
vA = 0,22*va (2).
Planteas la ecuación de Bernoulli para dos puntos situados sobre el eje de la tubería, cada uno debajo de uno de los tubos, y queda:
pA + (1/2)*δ*vA2 = pa + (1/2)*δ*va2, restas pa restas en (1/2)*δ*vA2 ambos miembros, y queda:
pA - pa = (1/2)*δ*va2 - (1/2)*δ*vA2 (3).
Luego, igualas las expresiones señaladas (1) (3) y queda la ecuación:
δ*g*h = (1/2)*δ*va2 - (1/2)*δ*vA2, multiplicas en todos los términos de la ecuación por 2/δ, y queda:
2*g*h = va2 - vA2, sumas vA2 y restas 2*g*h en ambos miembros, y queda:
vA2 = va2 - 2*g*h, sustituyes la expresión señalada (2) en el primer miembro, y queda:
(0,22*va)2 = va2 - 2*g*h, distribuyes la potencia en el primer miembro, y queda:
0,0484*va2 = va2 - 2*g*h, restas va2 en ambos miembros, y queda:
-0,9516*va2 = -2*g*h, divides por -0,9516 en ambos miembros, y queda:
va2 ≅ 2,102*g*h, reemplazas valores (g = 9,8 m/s2, h = 12 cm = 0,12 m), resuelves, y queda:
va2 ≅ 2,472, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
va ≅ 1,572 m/s, que es la rapidez con la que fluye el líquido en la parte más delgada de la tubería;
luego, reemplazas este valor en la ecuación señalada (2), resuelves, y queda:
vA ≅ 0,346 m/s, que es la rapidez con la que fluye el líquido en la parte más gruesa de la tubería,
por lo que puedes concluir que la opción señalada (d) es la respuesta correcta.
Espero haberte ayudado.
-
Buenas tardes, no entiendo este problema y me gustaría que me le expliczran. El problema es el siguiente:
Se realiza la experiencia de Torricelli con líquidos distintos en diferentes momentos. Calcular la altura del líquido en el tubo con respecto a la cubeta en los siguientes casos: a. El líquido es agua y el barómetro marca 765 mm. b. El líquido es ácido sulfúrico (d= 1,84 g/cm3) y la presión atmosférica es de 0,8 atmósferas.
muchas gracias.
Antonio Silvio Palmitano
el 28/8/18Recuerda la ecuación de equilibrio para esta experiencia:
δ*g*h = pat (1).
Luego, para el primer caso tienes:
δ1 = 1000 Kg/m3 (densidad del agua),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre),
h1 = 0,765 m (altura de la columna de agua en el barómetro),
pat1 = 101300 Pa (presión atmosférica normal).
Luego, para el segundo caso tienes:
δ2 = 1840 Kg/m3 (densidad del ácido sulfúrico),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre),
h2 = a determinar (altura de la columna de ácido sulfúrico en el barómetro),
pat2 = 0,8*101300 = 81040 Pa (presión atmosférica normal).
Luego, planteas la ecuación de equilibrio señalada (1) para ambos casos, y queda:
δ2*g*h2 = pat2,
δ1*g*h1 = pat1;
luego, divides miembro a miembro entre ambas ecuaciones, simplificas, y queda:
δ2*h2 / δ1*h1 = pat2 / pat1,
de aquí despejas:
h2 = pat2*δ1*h1 / δ2*pat1,
reemplazas valores, y queda:
h2 ≅ 81040*1000*0,765 / 1840*101300 ≅ 0,332609 m ≅ 33,2609 cm.
Espero haberte ayudado.
-
Buenas tardes, no entiendo este problema y me gustaría que me le expliczran. El problema es el siguiente:
Un cubo de madera de 20 cm de lado se encuentra flotando en agua. ¿Cuál es la altura de la parte emergente?. Densidad de la madera 600 Kg/ m3. Densidad del agua 1000 Kg/ m3.
muchas gracias.
Raúl RC
el 28/8/18Échale un vistazo a estos vídeos, el profe explica la teoria que necesitas ;)
https://www.youtube.com/watch?v=scO9JARtW4s
https://www.youtube.com/watch?v=-TdyQjiOAII
Antonio Silvio Palmitano
el 28/8/18Puedes llamar:
y a la altura sumergida del cubo,
0,20 m - y a la altura de la parte no sumergida del cubo.
Luego, tienes que el peso del cubo es:
P = δm*V*g = 600*0,203*10 = 48 N.
Luego, tienes que el peso del líquido desalojado por la parte sumergida del cubo es:
E = δa*Vs*g = 1000*0,202*(0,20 - y)*10 = 400*(0,20 - y) = 80 - 400*y (en Newtons).
Luego, a partir del Principio de Arquímedes, tienes la ecuación de equilibrio:
P = E, reemplazas valores, y queda:
48 = 80 - 400*y, sumas 40*y y restas 48 en ambos miembros, y queda:
400*y = 32, divides por 400 en ambos miembros, y queda:
y = 0,08 m = 8 cm.
Espero haberte ayudado.
-
Hola que tal, tengo este siguiente problema ... una pelota de base-ball abandona el bast a una altura de 0,90mts por encima del suelo formando un angulo de 35°con la horizontal y con una velocidad tal que el alcance horizontal hubiera sido de 120 mts. A la Distancia de 90 mts de la plataforma de lanzamiento se encuentra una valla de 8 mts de altura ¿Pasara la pelota por encima de la valla?. Cual es su velocidad? aceleracion? y Velocidad media ? si lo pueden resolver me ayudaria mucho gracias ....
Raúl RC
el 28/8/18Hola Miguel, la idea es que el trabajo duro sea el tuyo, te recomiendo le eches un vistazo a los vídeos sobre tiro parabolico, sobre los cuales versa tu duda, nos cuentas ;)
Tiro oblicuo o parabólico -
el ejercicio es el siguiente:
Una polea complicada consiste en cuatro esferas idénticas colocadas en los extremos de rayos que se prolongan desde un tambor giratorio. Una caja está unida a una cuerda delgada y ligera que se enrolla en el borde del tambor. Cuando se libera del reposo, la caja adquiere una rapidez V después de caer una distancia d. Ahora las cuatro esferas se mueven hacia adentro más cerca del tambor, y de nuevo la caja se suelta del reposo. Después de caer una distancia d, su rapidez será igua
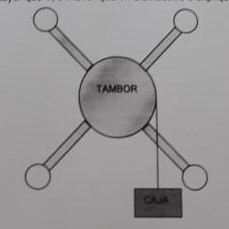 l a V, mayor que V, o menor que V? Demuestre o explique por qué.
l a V, mayor que V, o menor que V? Demuestre o explique por qué.Raúl RC
el 28/8/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Raúl RC
el 28/8/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
¿Alguien me puede ayudar con el siguiente problema de la fuerza de Coriolis? No se por donde empezar.
En un punto de coordenadas: 36ºN 7ºW , se ha detectado una masa de agua que se mueve con una velocidad de 0.20 m/s y dirección E.
Determinar el módulo y dirección de la aceleración de Coriolis. Interpretar.
Gracias
Raúl RC
el 27/8/18! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Hola, No puedo hacer que mi resultado en este problema coincida con la real, ¿Está bien mi forma de hacerlo? (Problema 17)




Diaz Daniel Victor
el 28/8/18Hola David la altura que calculaste en el ítem A solo es la altura que tendrá el cohete al transcurrir los 1,50 min. necesitas averiguar cual es su velocidad final al terminar el combustible osea cuando terminan los 1,50 min y tomar esa como su velocidad inicial para continuar desplazándose, luego sumas las dos alturas que necesitas y tenes la altura máxima... con respecto al tiempo nos dice que no influye la resistencia del aire ni la gravedad así que tenés que calcular solo el tiempo de caída y multiplicar por 2 ya que el tiempo de subida es el mismo que el tiempo de caída.
-
Antonio Silvio Palmitano
el 27/8/18Observa que sobre el cilindro actúan dos fuerzas con dirección vertical:
Peso, con sentido hacia abajo,
Empuje, con sentido hacia arriba;
luego, planteas la condición de equilibrio, y queda:
P = E,
por lo que tienes que el módulo de la fuerza de flotación es igual al módulo del peso del cuerpo sumergido.
Luego, reemplazas el valor del módulo de la fuerza de flotación para el primer cilindro, y queda:
P = 3,72 N, que es el valor del módulo del peso del primer cilindro.
Luego, expresas al módulo del peso del cilindro en función de su densidad de masa (δ), del diámetro de su base (d), y de su altura (H), y la ecuación queda:
(1/4)*δ*d2*g*H = 3,72 N (1).
Luego, multiplicas por 1/2 en ambos miembros de la ecuación señalada (1), y queda:
(1/4)*δ*d2*g*H * (1/2) = 3,72 N * (1/2),
asocias los dos últimos factores en el primer miembro, resuelves el segundo miembro, y queda:
(1/4)*δ*d2*g*(H/2) = 1,86 N,
y observa que en el primer miembro tienes la expresión del módulo del peso del segundo cilindro, y como éste valor es igual al módulo de la fuerza de flotación según muestra la condición de equilibrio, puedes concluir que el módulo de la fuerza de flotación para el segundo cilindro es:
E ' = 1,86 N.
Espero haberte ayudado.

























