-
melody perez
el 6/8/18 -
Juan Ignacio Acevedo Cantillana
el 6/8/18
Hola, necesito un poco de ayuda con este problema
Raúl RC
el 7/8/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Agustina Sabatini
el 4/8/18Hola, Necesito ayuda con estos dos problemas.
Si el contenido inicial del cadmio en cierta agua es de 0,0461 mg/l Determina la concentración final de cadmio que resulta por el enfriamiento-evaporación si se hace circular un caudal de 20 kg/s de agua a través de una torre de enfriamiento.Considere que el agua ingresa a una temperatura de 29grados centígrados y sale de la torre a 20grados centígrados (expresar en metros cúbicos por hora)
Calor de valorización 2257 Kl/kg (539,4kcal/kg)
Según un estudio en http://digital.un u.edu.ar/objetos digitales/5317/norgo-final.pdf. el 33%de los elaboradores de aceitunas de la Provincia de Mendoza utiliza balsas de evaporación como forma de tratar el agua residual .Un agua residual puede contener 1462mg/l de potasio .Cierta empresa ,posee una pileta que contiene 50.000litros de efluente .Determina como variará la concentración del potasio en la pileta si
a)se evapora 15000litros se afluente.
b)Como consecuencia de una lluvia ,se agregan 5m cubicos de agua de lluvia (después de la evaporacion)
¡Gracias!
-
JOSE MORENO CHAICHIO
el 3/8/18Hola necesito ayuda en un ejercicio de física 4 eso;
Arrastramos un bloque una distancia de 20 metros por un plano horizontal. Realizamos un trabajo para ello de 1500 Julios, que se utiliza para vencer a la fuerza de rozamiento. Calcula el valor de la fuerza de rozamiento.
Gracias por la ayuda.
Antonio Silvio Palmitano
el 3/8/18Considera que la fuerza es paralela y de igual sentido que el desplazamiento del cuerpo, luego planteas la expresión de su trabajo mecánico, y queda:
F*Δs = WF, divides en ambos miembros por Δs, y queda:
F = WF/Δs, reemplazas valores, y queda:
F = 1500/20 = 75 N, que es el módulo de la fuerza aplicada.
Luego, planteas el trabajo de la fuerza de rozamiento (observa que es paralela al desplazamiento del cuerpo, pero con sentido opuesto), y queda:
Wfr = -fr*Δs (1);
luego, si consideras que el cuerpo estaba en reposo tanto al inicio como al final de su recorrido, tienes que la variación de su energía cinética de traslación es igual a cero; y como se desplaza sobre una superficie rugosa horizontal, también tienes que la variación de su energía potencial gravitatoria es igual a cero.
Luego, planteas la ecuación trabajo-energía, y queda:
WF + Wfr = ΔEC + ΔEP,
cancelas los dos términos del segundo miembro (observa que son iguales a cero), y queda:
WF + Wfr = 0,
restas WF en ambos miembros, y queda:
Wfr = -WF,
sustituyes la expresión señalada (1) en el primer miembro, y queda:
-fr*Δs = -WF,
divides en ambos miembros por -Δs, y queda
fr = WF/Δs,
reemplazas los datos que tienes en tu enunciado, y queda:
fr = 1500/20 = 75 N,
que es el valor del módulo de la fuerza de rozamiento (observa que este módulo es igual al módulo de la fuerza aplicada que ya hemos calculado).
Espero haberte ayudado.
-
Mer
el 3/8/18Hola, necesito ayuda para comprobar los apartados f y g porque a mí me dan resultados diferentes.
Muchas gracias
Antonio Silvio Palmitano
el 3/8/18Tienes la expresión de la función de posición:
x(t) = 16 - 12*t + 2*t2 (1).
f)
Evalúas la expresión de la función señalada (1) para los valores indicados en tu enunciado, y quedan:
x(-1) = 16 - 12*(-1) + 2*(-1)2 = 16 - 12 + 2*1 = 16 - 12 + 2 = 6 m,
x(3) = 16 - 12*(3) + 2*(3)2 = 16 - 36 + 2*9 = 16 - 36 + 18 = -2 m;
luego, planteas la expresión de la velocidad media, y queda:
vm = ( x(3) - x(1) ) / ( 3 - (-1) ) = ( -2 - 6 ) / ( 3 + 1 ) = -8 / 4 = -2 m/s.
g)
Evalúas la expresión de la función señalada (1) para los valores indicados en tu enunciado, y quedan:
x(0) = 16 - 12*(0) + 2*(0)2 = 16 - 0 + 2*0 = 16 - 0 + 0 = 16 m,
x(6) = 16 - 12*(6) + 2*(6)2 = 16 - 72 + 72 = 16 - 0 + 0 = 16 m;
luego, planteas la expresión de la velocidad media, y queda:
vm = ( x(6) - x(0) ) / ( 6 - 0 ) = ( 16 - 16 ) / ( 6 - 0 ) = 0 / 6 = 0 m/s.
Espero haberte ayudado.
-
CJB
el 3/8/18Alguien me puede ayudar con este ejercicio? Gracias de antemano :D
Antonio Silvio Palmitano
el 3/8/18Observa que tienes la gráfica de la velocidad en función del tiempo, y observa que es una parábola cuyo eje es paralelo al eje OV, y cuyo vértice es el punto (0,0), y que pasa por los puntos (-10,1000) y (10,1000).
Luego, planteas la ecuación cartesiana explícita de una parábola de estas características, y queda:
v = a + b*t + c*t2 (1),
reemplazas las coordenadas de los puntos conocidos, resuelves coeficientes, y queda el sistema de tres ecuaciones lineales con tres incógnitas:
0 = a,
1000 = a - 10b + 100c,
1000 = a + 10b + 100c;
luego, reemplazas el valor remarcado en las dos últimas ecuaciones, cancelas términos nulos, divides en ambas por 10 en todos sus términos, y queda:
100 = -b + 10c (2),
100 = b + 10c (3);
luego, restas miembro a miembro entre ambas ecuaciones, y queda:
0 = -2b, divides por -2 en ambos miembros, y queda: 0 = b;
luego, reemplazas este valor remarcado en las ecuaciones señaladas (2) (3), cancelas términos nulos, y observa que para ambas queda
100 = 10c, divides por 10 en ambos miembros, y queda: 10 = c;
luego, reemplazas los valores remarcados en la expresión de la función velocidad señalada (1), cancelas términos nulos, y queda:
v(t) = 10*t2 (4) (en cm/s).
Luego, derivas la expresión señalada (4) con respecto al tiempo, y queda:
dv/dt = 20*t,
por lo que tienes que la expresión de la aceleración en función del tiempo queda:
a(t) = 20*t (en cm/s2).
Luego, integras la expresión señalada (4) con respecto al tiempo, y queda:
∫ v(t)*dt = (10/3)*t3 + C,
por lo que tienes que la expresión general de la posición en función del tiempo queda:
x(t) = (10/3)*t3 + C (5);
luego, tienes la condición inicial de tu enunciado:
x(3) = 0,
sustituyes la expresión evaluada de la función en el primer miembro, y queda:
(10/3)*33 + C = 0, resuelves el primer término, y queda:
90 + C = 0, restas 90 en ambos miembros, y queda:
C = -90, reemplazas este valor en la expresión de la función posición señalada (5), y queda:
x(t) = (10/3)*t3 - 90 (en cm).
Espero haberte ayudado.
-
Deidara Stick.
el 3/8/18Buenas tardes alguien me podria ayudar con el problema enunciado, no he logrado resolverlo.
* Los bloques A y B pesan respectivamente 150N y 300N y están conectados mediante una cuerda, los coeficientes de rozamiento cinético son 0,20 para A y 0,15 para B. La fuerza F aplicada es 200N
Determinar:
a.) La aceleración de B
b.) La velocidad de A y B al cabo de 5 segundos
De antemano muchas gracias
Raúl RC
el 5/8/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
Antonio Silvio Palmitano
el 5/8/18Si consideras que la cuerda y las poleas son ideales, entonces tienes que la tensión de la cuerda es F.
Luego, para el bloque B, considera un eje de posiciones OX horizontal con sentido positivo hacia la izquierda, aplicas la Segunda Ley de Newton, y tienes la ecuación (te dejo el planteo para las fuerzas perpendiculares a este eje que actúan sobre este cuerpo):
2*F - frB = MB*aB, (1).
Luego, para el bloque A, considera un eje de posiciones OX horizontal con sentido positivo hacia la derecha, aplicas la Segunda Ley de Newton, y tienes la ecuación (te dejo el planteo para las fuerzas perpendiculares a este eje que actúan sobre este cuerpo):
2*F - frA = MA*aA (2).
Luego, planteas las expresiones de las masas de los bloques en función de los módulos de sus pesos y del módulo de la aceleración gravitatoria terrestre (observa que consideramos: g = 10 m/s2), y quedan:
MB = PB/g = 300/10 = 30 Kg,
MA = PA/g = 150/10 = 15 Kg.
Luego, planteas las expresiones de los módulos de las fuerzas de rozamiento que actúan sobre los bloques, y quedan:
frB = μB*MB*g = 0,15*30*10 = 45 N,
frA = μA*MA*g = 0,20*15*10 = 30 N.
Luego, reemplazas valores en las ecuaciones señaladas (1) (2), y queda:
2*200 - 45 = 30*aB,
2*200 - 30 = 15*aA,
resuelves los primeros miembros en ambas ecuaciones, divides por 30 en la primera y por 15 en la segunda, y queda:
11,833 m/s2 ≅ aB,
24,667 m/s2 ≅ aA.
Luego, si consideras que los bloques estaban inicialmente en reposo, planteas la ecuación de velocidad de Movimiento Rectilíneo Uniformemente Acelerado para ambos móviles, y queda:
vB = aB*t ≅ 11,833*5 ≅ 59,165 m/s,
vA = aA*t ≅ 24,667*5 ≅ 123,335 m/s.
Espero haberte ayudado.
-
Marilú Ayay Leyva
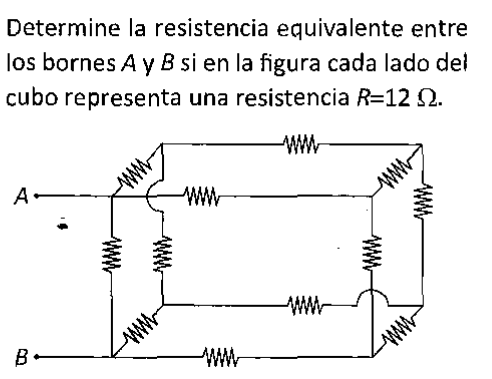
el 3/8/18Buenas tardes, me podría ayudar con este ejercicio, por favor.
Es muy urgente.
Agradezco infinitamente
Saludos.
Raúl RC
el 5/8/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Jeishler Da Alvarado
el 2/8/18Necesito ayuda con ejercicio de circuito con mallas.
Buenas tardes, hoy el profesor nos mandó un lista de ejercicios y nos dijo que para el examen de mañana nos pondría 1 ej idéntico de los de la lista y otro no. Es decir que si resuelvo todos los de la lista tengo 10 puntos de 20 asegurados jaja. La mayoría de ejercicios los pude resolver sin problemas, el tema es circuitos con mallas. La mayoría de ejercicios simplemente hay que ubicar las mallas, crear las ecuaciones, despejar y encontrar las corrientes. Pero hubo un ejercicio que no he terminado por una duda.
El ejercicio es con dos mallas y me piden calcular i1, i2, VR3 y VC, así que hice lo de siempre y saqué las dos ecuaciones y con eso calculé las dos corrientes i1 e i2, pero ahora no sé cómo calcular a V en R3, porque la formula que me sé es que VR3= i3 . R3 pero en este caso no hay i3, entonces cómo sería la formula? porque tanto i2 como i1 influyen en R3, además tampoco sé la formula para calcular el voltaje en el punto C ---> VC . Aquí les dejo las fotos del ejercicio y de lo que he hecho, si alguien me ayuda lo agradecería mucho, es el único ejercicio que me falta.
Raúl RC
el 5/8/18Lamento no poderte ayudar con este ejercicio, lo único que puedo decirte es que el profe grabó un vídeo sobre el tema de las leyes de Kirchoff correspondientes a fisica universitaria, espero pueda servirte
Leyes de Kirchhoff -
JOSE MORENO CHAICHIO
el 2/8/18Necesito ayuda para este problema:
Un submarino tiene una masa de 120 Tm y un volumen de 140 m3, este submarino incluye un depósito de 50 m3, ¿Qué volumne máximo de agua puede contener este depósito para que el submarino flote? Densidad de agua marina 1050 kg/m3
gracias
Antonio Silvio Palmitano
el 2/8/18Puedes llamar X a la masa de agua marina que tienes en el depósito, con el submarino a flote entre dos aguas.
Luego, observa que sobre el submarino actúan dos fuerzas verticasles, de las que indicamos sus módulos y sentidos:
Peso total: P = 120000 + 1050*X*g (en Newtons), hacia abajo;
Empuje del agua: E = 1050*140*g = 147000*g (en Newtons), hacia arriba.
Luego, plantea la condición de equilibrio (consideramos el sentido hacia arriba como positivo):
P - E = 0, sumas E en ambos miembros, y queda:
P = E, sustituyes expresiones, y queda:
120000 + 1050*X*g = 147000*g, restas 120000 en ambos miembros, y queda:
1050*X*g = 147000*g - 120000,
reemplazas el valor de la aceleración gravitatoria terrestre (observa que considerarmos: g = 10 m/s2), resuelves términos, y queda:
10500*X = 1470000 - 120000, resuelves el segundo miembro, y queda:
10500*X = 1350000, divides por 10500 en ambos miembros, y queda:
X ≅ 128,571 Kg.
Espero haberte ayudado.
