-
Holaaa! podrían ayudarme con este ejercicio?
Por lo que tengo entendido , si es vc, entonces es m.r.u , Así que hice dx= vx.t , y de ahí saque el tiempo. Luego hice en el eje y , por lo que hice la ecuación de velocidad final , vfy= voy+g.t. voy=0 , pero hay algo que estoy haciendo mal.

Antonio Silvio Palmitano
el 2/8/18Plantea un sistema de referencia con eje OX al nivel del agua, con sentido positivo acorde al desplazamiento del tanque, con origen de coordenadas en la posición que corrsponde al muelle, y con eje OY vertical, con sentido positivo hacia arriba, con instante inicial (ti = 0).
Luego, tienes los datos correspondientes al tanque:
xi = 2 m, y = 0 (constante), vT = 0,5 m/s (horizontal, constante);
luego, planteas para este móvil las ecuaciones de posición de Movimiento Rectilíneo Uniforme, y queda:
xT = 2 + 0,5*t (1),
yT = 0 (2).
Luego, tienes los datos iniciales correspondientes a la piedra:
xi = 0, yi = 3 m, vxPi = a determina, vyPi = 0, a = -g = -10m/s2 (vertical);
luego, planteas para este móvil las ecuaciones de Movimiento Rectilíneo Uniformemente Acelarado (Movimiento Parabólico), cancelas términos nulos, resuelves coeficientes, y queda:
xP = vxPi*t (3),
yP = 3 - 5*t2 (4).
Luego, planteas la condición de encuentro, y queda:
xT = xP (5),
yT = yP (6);
sustituyes las expresiones señaladas (1) (2) (3) (4) en las ecuaciones señaladas (5) (6), y queda:
2 + 0,5*t = vxPi*t (7),
0 = 3 - 5*t2 (8),
sumas 5*t2 en ambos términos de la ecuación señalada (8), divides por 5 en ambos miembros, y queda:
t2 = 0,6, extraes raíz cuadrada en ambos miembros (observa que elegimos la raíz positiva), y queda:
t ≅ 0,775 s, que es el valor del instante de encuentro de los dos móviles;
luego, reemplazas este valor en la ecuación señalada (7), y queda:
2 + 0,5*0,775 ≅ vxPi*0,775, resuelves el primer miembro, divides en ambos miembros por 0,775, y queda:
3,082 m/s ≅ vxPi, que es el valor del módulo de la velocidad inicial de la piedra.
Luego, reemplazas el valor remarcado en las ecuaciones señaladas (1) (2), y queda:
xT ≅ 2 + 0,5*0,775 ≅ 2,387 m,
yT = 0;
luego, reemplazas los dos últimos valores remarcados en las ecuaciones señaladas (5) (6), y queda:
2,387 m ≅ xP,
0 = yP.
Luego, tienes que si el módulo de la velocidad inicial de la piedra es: vxPi ≅ 3,082 m/s, entonces la piedra y el tanque se encuentran en el punto cuyas coordenadas son: x ≅ 2,387 m, y = 0.
Espero haberte ayudado.
-
Me podeis resolver estos 2 ejercicios por favor , es que por mas que lo intento no me sale
Ejercicio 8
Se cae un coche de 1500kg de una montaña rusa desde una altura de 23 metros por un camino (vias de la montaña rusa) sin fuerza de rozamiento. Cuando el coche se pone boca abajo en el punto mas alto de una circunferia cuyo diametro es de 15 metros . Calcular la fuerza que hace el camino (vias de la montaña rusa) sobre el coche
Respuesta : 1,7x10^4N
Tener en cuenta el dibujo del ejer 8

Ejercicio 1
Un bloque de 6kg sin fuerza de rozamiento cae por una cuesta del punto A al punto B . Una vez sobrepasado el punto B el bloque se para a 2,5 metros como consecuencia de la fuerza de rozamiento. Calcular el coeficiente de la fuerza de rozamiento entre la tierra y el bloque.
Respuesta : 0,40
Tener en cuenta el dibujo del ejer 1
Raúl RC
el 2/8/18Dudas concretas por favor
se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) envies dudas concretas, muy concretas. Y que nos envies también todo aquello que hayas conseguido hacer por ti mismo. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber cuál es tu nivel, en que podemos ayudarte, cuales son tus fallos.... Recuerda que el trabajo duro ha de ser tuyo. Nos cuentas ¿ok
-
Buen día, me podría x favor alguien ayudarme con el problema enunciado
× Un camión está viajando a una velocidad de 60 mph, cuando de repente el conductor aplica los frenos para terminar llevando al camión en reposo.
La desaceleración del camión es constante y el mismo recorre una distancia de 350 pies, cuando se detiene.
Determine cuál es el mínimo coeficiente de fricción estatico entre el cajón A y la superficie de la plataforma horizontal del camión de forma que el cajón no deslize sobre la superficie.
Gracias
Antonio Silvio Palmitano
el 1/8/18Tienes los datos:
vi = 60 mi/h = 60*5280 / 3600 ≅ 88 pie/s (módulo de la velocidad inicial del camión),
vf = 0 (módulo de la velocidad final del camión),
s = 350 pie (distancia de frenado del camión);
y con ellos puedes plantear la expresión de su aceleración (observa que consideramos como positivo el sentido de desplazamiento del camión):
a = (vf2 - vi2) / (2*s), reemplazas datos, resuelves, y queda:
a ≅ -11,063 pie/s2.
Luego, observa que sobre el cajón actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos (observa que indicamos con M a la masa del cajón, y que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 32 pie/s2):
Peso: P = M*g, vertical hacia abajo,
Acción normal del camión: N, vertical hacia arriba,
Rozamiento del camión: fre = μe*N, horizontal, contraria al desplazamiento del camión);
luego, planteas la Segunda Ley de Newton (observa que consideramos positivo el sentido hacia arriba para las fuerzas verticales), y queda el sistema de ecuaciones:
-fre = M*a, aquí sustituyes la expresión del módulo de la fuerza de rozamiento, y queda: -μe*N = M*a (1),
N - P = 0, aquí sumas P en ambos miembros, sustituyes su expresión, y queda: N = M*g (2);
luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
-μe*M*g = M*a, aquí divides por -M*g en ambos miembros, simplificas, y queda:
μe =-a/g;
luego, reemplazas los valores remarcados, resuelves, y queda:
μe ≅ 0,346.
Espero haberte ayudado.
-
Hola, me podeis resolver este problema por favor.
Un objeto de 0,3 kg está unido a una cuerda de 1,5m. Cuando la velocidad está a 200 vueltas por minuto se rompe la cuerda. ¿Cual es la tensión maxima que la cuerda? (Espero que se entienda bien, lo he tenido que traducir del euskera al castellano 😊)
GRACIAS
-
Necesito ayuda con el siguiente problema:
Una partícula describe un m.a.s con un perido de 2s. En el instante inicial se encuentra a 3cm del origen, se acerca a 5cm/s:
a) Escribe las ecuaciones del movimiento
b) Calcula la velocidad y acceleración máximas
c) Determinar x, v y a cuando t=0,5s.
Se qué fórmulas tengo que utilizar, pero no se como calcular la amplitud. Supongo que los 5cm/s es la velocidad
-
buenos dias, necesito ayuda con este ejercicio. hice la parte a) pero no se si esta bien y la parte B) no se como resolverla. A continuacion escribo el enunciado.
sean dos esferas concentricas una maciza y la otra hueca. la primera tiene un radio de 2 cm y esta uniformemente cargada en todo su volumen con una densidad de carga de -4.10 ^-6 c/m3. La esfera hueca de radio interior 5 cm y radio exterior 8 cm es un conductor descargado. determinar la expresion de : a) campo electrico en todas las regiones del espacio. b) el potencial electrico en todas las regiones explicitando cual es el referencial utilizado
Raúl RC
el 31/7/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Buenos dias, alguien me podria ayudar:
Dos cuerpos, con masa m y 2m, se unen por medio de una cuerda inextensible y ligera que pasa sobre una polea lisa. Despues de 4s, un cuerpo con masa m es unido de repente al cuerpo que asciende. Encuentrse (a) la velocidad y (b) que energia cinetoca pierde el cuerpo que desciede cuando se añade el cuespo con masa m.
//hay que considerar que la union de las dos masas es instantanea y que es un choque inelastico.
Raúl RC
el 31/7/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Hola! Alguien me podría ayudar con el siguiente problema?
En un m.a.s, la velocidad máxima es de 40m/s, y la acceleración máxima, 45m/s^2. Calcula la frecuencia y amplitud de las oscilaciones.
La amplitud ya la he calculado, me da: A= 35,56m, y tambien tengo calculada w= 1,12. Se que la frecuencia es 1/T, por tanto, mi incógnita es T y no se cómo calcularla. Alguien me podría ayudar?
Gracias!
-
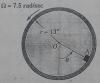
Hola .. disculpas.
Alguien de x favor podría ayudarme con el siguiente exercise.. lo necesito please..
// Un tambor rota sobre un eje horizontal con una velocidad angular constante de 7,5 rad/seg.- Un pequeño bloque A en el interior del tambor no tiene movimiento relativo con la superficie del mismo. Determine el coficiente de fricción estático en función del ángulo θ
Muchas gracias de antemano a esa persona que me brinde ayuda !!
Grazie... Mil gracias
Raúl RC
el 31/7/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Unicoos llega exclusivamente hasta secundaria y bachillerato
-
Necesito ayuda con el siguiente problema:
Una partícula describe un m.a.s con un perido de 2s. En el instante inicial se encuentra a 3cm del origen, se acerca a 5cm/s:
a) Escribe las ecuaciones del movimiento
b) Calcula la velocidad y acceleración máximas
c) Determinar x, v y a cuando t=0,5s.
Se qué fórmulas tengo que utilizar, pero no se como calcular por ejemplo phi inicial. O w.
Muchísimas gracias!
Antonio Silvio Palmitano
el 30/7/18Vamos con una orientación.
Tienes los datos generales:
A = 5 cm (amplitud de oscilación),
T = 2 s (periodo de oscilación);
luego, planteas la expresión del coeficiente angular (pulsación) en función del período, y queda:
ω = 2π/T = 2π/2 = π rad/s.
Luego, puedes considerar la expresión de la función de elongación:
x = A*sen(ω*t + δ) (observa que la función seno es creciente en el intervalo: (-π/2,π/2),
reemplazas valores, y queda:
x = 5*sen(π*t + δ) (1).
Luego, tienes los datos iniciales:
t = 0 (instante inicial),
x = 3 cm (con la elongación aumentando hacia su máximo valor),
reemplazas valores en la expresión de la función de elongación señalada (1), y queda la ecuación:
3 = 5*sen(π*0 + δ), divides en ambos miembros por 5, resuelves el argumento del seno, y queda:
0,6 = sen(δ), compones en ambos miembros con la función inversa del seno, y queda:
36,870° ≅ δ, expresas a este valor en radianes, y queda:
36,870°*π/180° ≅ δ, resuelves el primer miembro, y queda:
0,205π rad ≅ δ, que es el valor de la fase inicial;
luego, reemplazas en la expresión de la función de elongación señalada (1), y queda:
x = 5*sen(π*t + 0,205π) (2), que es la expresión completa de la función de elongación.
Luego, puedes considerar la expresión de la función de velocidad:
v = ω*A*cos(ω*t + δ),
reemplazas valores, resuelves el coeficiente, y queda:
v = 1,025*cos(π*t + 0,205π) (3),
que es la expresión de la función velocidad.
Luego, puedes continuar la tarea.