-
Hola, buenas tardes. ¿Me pueden sacar de esta duda. por favor? Es un ejericicio de Campo electrico.
Es el que dice "La figura A...." ¿Cuál de los campos es mayor, menor o igual? Yo consideré que el Campo de A es mayor que el de B.
-
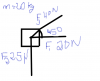
Hola, a ver si me podeis explicar este problema, gracias: tres amigos juegan ca tirar de una caja se el esquema.
¿Cual será la fuerza resultante? ¿y la aceleración de la caja?
Antonio Silvio Palmitano
el 12/7/18Entendemos que el dibujo corresponde a una vista "desde arriba".
Luego, establece un sistema de referencia con origen de coordenadas en el centro de la caja, con eje OX con dirección y sentido positivo acordes con la fuerza F1, y con eje OY perpendicular al eje anterior, con sentido positivo hacia arriba según el dibujo que muestra tu imagen.
Luego, observa que las componentes de las fuerzas son:
F1x = 20 N,
F1y = 0;
F2x = 0,
F2y = -25 N;
F3x = F3*cos(45°) = 40*cos(45°) = 40*√(2)/2 = 20*√(2) N ≅ 28,242 N,
F3x = F3*sen(45°) = 40*sen(45°) = 40*√(2)/2 = 20*√(2) N ≅ 28,242 N.
Luego, planteas las expresiones de las componentes de la fuerza resultante (R), y queda:
Rx = F1x + F2x + F3x = 20 + 0 + 20*√(2) = ( 20 + 20*√(2) ) N ≅ 48,242 N,
Ry = F1y + F2y + F3y = 0 - 25 + 20*√(2) = ( -25 + 20*√(2) ) N ≅ 3,242 N.
Luego, planteas la expresión del cuadrado del módulo de la fuerza resultante, y queda:
R2 = Rx2 + Ry2 = ( 20 + 20*√(2) )2 + ( -25 + 20*√(2) )2,
desarrollas los cuadrados en los términos, y queda:
R2 = 400 + 800*√(2) + 800 + 625 - 1000*√(2) + 800,
reduces términos semejantes, y queda:
R2 = 2625 - 200*√(2),
Extraes raíz cuadrada en ambos miembros, y queda:
R = √( 2625 - 200*√(2) ) N ≅ 48,396 N.
Luego, planteas la expresión de la tangente del ángulo de inclinación de la fuerza resultante con respecto al semieje OX positivo, y queda:
tanθ = Ry/Rx = ( -25 + 20*√(2) ) / ( 20 + 20*√(2) ) ≅ 0,068,
compones con la función inversa de la tangente, y el valor aproximado del ángulo de inclinación queda:
θ ≅ 3,891°.
Luego, planteas la expresión del módulo de la aceleración en función del módulo de la fuerza resultante y de la masa de la caja, y queda:
a = R/M = √( 2625 - 200*√(2) ) / 20 m/s2 ≅ 2,420 m/s2,
y observa que la fuerza resultante y la aceleración tienen el mismo ángulo de inclinación.
Espero haberte ayudado.
JOSE MORENO CHAICHIO
el 13/7/18 -
Un esquiador inicia un salto horizontal con una velocidad inicial de 10 m/s, a una altura de 80 m., con respecto al suelo:
1. Hallar el tiempo que tarda en esquiador en el aire.
2. El alcance o recorrido horizontal (dx).
3. Los componentes vertical y horizontal de la velocidad (vx y vy)
4. La velocidad final, conque llega al suelo.
Antonio Silvio Palmitano
el 12/7/18Considera un sistema de referencia con eje OX paralelo al suelo, con sentido positivo acorde al desplazamiento del esquiador, con eje OY perpendicular al suelo, con sentido positivo hacia arriba y que pasa por el punto inicial del salto (observa que el origen de coordenadas está a nivel del suelo), con instante inicial (ti = 0) correspondiente al inicio del movimiento, y considera que el módulo de la aceleración gravitatoria terrestre es: g = 10 m/s2.
Luego, tienes los datos iniciales:
xi = 0, yi = 80 m, vix = 10 m/s, viy = 0, ax = 0, ay = -10 m/s2.
Luego, planteas las ecuaciones de posición y de velocidad de Movimiento Parabólico, y quedan:
x = vix*t,
y = yi + viy*t + (1/2)*ay*t2,
vx = vix,
vy = viy - ay*t;
luego, reemplazas datos, cancelas términos nulos, resuelves coeficiente, y queda:
x = 10*t (1),
y = 80 - 5*t2 (2),
vx = 10 m/s (3),
vy = -10*t (4).
1) y 2)
Planteas la condición de alcance (x = a determinar, y = 0), reeplazas en las ecuaciones señaladas (1) (2) y queda el sistema
x = 10*t,
0 = 80 - 5*t2, de aquí despejas (observa que elegimos la solución positiva): t = 4 s;
luego, reemplazas en la primera ecuación, resuelves, y queda: x = 40 m;
por lo que tienes que el instante final es t = 4 s, por lo que el esquiador permanece cuatro segundos en el aire, y también tienes que su posición final (o alcance) es cuarenta metros.
3)
Reemplazas el valor del instante final en las ecuaciones señaladas (3) (4) (en realidad, solo en la segunda de ellas), resuelves, y queda:
vx = 10 m/s,
vy = -20 m/s;
que son las componentes de la velocidad del esquiador cuando éste está a punto de tocar el suelo.
4)
Luego, planteas la expresión del módulo de la velocidad final del esquiador, y queda:
v = √(vx2 + vy2) = √( 102 + (-20)2 ) = √(100 + 400) = √(500) = 10√(5) m/s ≅ 22,361 m/s.
Espero haberte ayudado.
-
Buenas tardes.
Tengo dudas sobre Fisica.¿ Alguien me podria explicar/ayudar con la equacion de dimensiones y el analisis dimensional?
Ejemplos que me podrian ayudar : Superficie, volumen, densidad y velocidad.
Muchas gracias
-
Buenas, no es una pregunta sobre un ejercicio en concreto, os cuento: no he dado física en 2º de bachiller y me gustaria tener al menos las bases para la carrera que quiero hacer (Ing. Química). ¿Por donde debería de empezar?
-
Hola buenas.. tengo un problema con un ejercicio de fisica de capacitancia y dielectricos si alguien conoce del tema y me pueda ilustrar porque me trabo un poco.
un cascaron esferico conductor tiene radio interno a y exterior c. El espacio entre las 2 superficies se llena con un dielectrico de constante k1 entre a y b y k2 entre b y c. Determine la capacidad del sistema
Antonio Silvio Palmitano
el 11/7/18Vamos con una orientación.
Puedes considerar una serie de dos capacitores esféricos, uno con radio interior a y radio exterior b (con su dieléctrico de constante κ1), y otro con radio interior y radio exterior c (con su dieléctrico de constante κ2),
y observa que en este modelo los dos capacitores comparten una superficie esférica que los limita, que podríamos suponer es una lámina esférica conductora ideal de radio b.
Luego, solo queda que plantees las expresiones de las dos capacidades, y que plantees luego la expresión de la capacidad equivalente.
Espero haberte ayudado.
-
Hola, necesito ayuda con este problema de física:
"Un niño se asoma por la ventana de su edificio ubicada a una altura H medida desde la acera. Primero deja caer una piedra y un segundo después arroja verticalmente hacia abajo una segunda piedra con una rapidez inicial de 15 m/s. Se observa que las dos piedras impactan de manera simultánea con la acera. Determine el valor de H. Considere g= 10 m/s2."
Gracias
Antonio Silvio Palmitano
el 11/7/18Considera un sistema de referencia con eje OY vertical, con origen a nivel del suelo, con sentido positivo hacia arriba, y con instante inicial correspondiente al momento en que deja caer la primera piedra.
Luego, considera la ecuación de posición de Movimiento Rectilíneo Uniformemente Variado (observa que consideramos a la aceleración como a = -g):
y = yi + vi*(t-ti) - (1/2)*g*(t-ti)2.
Luego, tienes los datos para la primera piedra:
ti = 0, yi = H, vi = 0, g = 10 m/s2,
reemplazas en la ecuación de posición, cancelas términos nulos, resuelves coeficientes, y queda:
y1 = H - 5*t2 (1).
Luego, tienes los datos para la segybda piedra:
ti = 1 s, yi = H, vi = -15 m/s, g = 10 m/s2,
reemplazas en la ecuación de posición, cancelas términos nulos, resuelves coeficientes, y queda:
y2 = H - 15*(t-1) - 5*(t-1)2 (2).
Luego, planteas la condición de llegada al suelo en forma simultánea para ambas piedras:
y1 = 0, y2 = 0, t = a determinar,
remplazas en las ecuaciones señaladas (1) (2), y queda el sistema de dos ecuaciones con dos incógnitas:
0 = H - 5*t2, aquí sumas 5*t2 en ambos miembros, y queda: 5*t2 = H (3),
0 = H - 15*(t-1) - 5*(t-1)2 (4);
luego, sustituyes la expresión señalada (3) en la ecuación señalada (4), desarrollas términos, y queda:
0 = 5*t2 - 15*t + 15 - 5*t2 + 10*t - 5,
cancelas términos opuestos, reduces términos semejantes, y queda:
0 = -5*t + 10, aquí sumas 5*t en ambos miembros, y queda:
5*t = 10, divides por 5 en ambos miembros, y queda:
t = 2 s, que es el instante en que las dos piedras tocan el suelo;
luego, reemplazas el valor remarcado en la ecuación señalada (3), y queda:
5*22 = H, resuelves el primer miembro, y queda:
20 m = H, que es la posición inicial de las piedras;
luego, a fin de verificar, reemplazas el valor del instante final remarcado en la ecuación señalada (4), resuelves términos, y queda:
0 = H - 15 - 5, aquí sumas 20 en ambos miembros, y queda: 20 m = H.
Espero haberte ayudado.
-
Hola buenas tardes, necesito ayuda con este problama de física. Ayudarme porfavor.

Antonio Silvio Palmitano
el 10/7/18Establece un sistema de referencia con origen en el punto de lanzamiento, con eje OX paralelo al suelo y con sentido positivo acorde al desplazamiento del proyectil, con eje OY vertical con sentido positivo hacia arriba, y con instante inicial ti = 0 coincidente con el instante de lanzamiento.
Luego, planteas las ecuaciones de posición y de velocidad de Tiro Oblicuo (observa que reemplazamos valores y que consideramos que el módulo de la aceleración gravitatoria terrestre es 10 m/s2), y queda:
x = 300*cosθ*t (1),
y = 300*senθ*t - (1/2)*10*t2, aquí resuelves coeficientes, y queda: y = 300*senθ*t - 5*t2 (2);
vx = 300*cosθ (3),
vy = 300*senθ - 10*t (4).
a)
Tienes la condición de alcance en tu enunciado: x = 5000 m, y = 0, reemplazas en las ecuaciones señaladas (1) (2), y queda el sistema:
5000 = 300*cosθ*t (5),
0 = 300*senθ*t - 5*t2, aquí extraes factor común, y queda:
0 = t*(300*senθ - 5*t), y por anulación de un producto tienes dos opciones:
1)
t = 0, que corresponde al instante inicial,
2)
300*senθ - 5*t2 = 0, y de aquí despejas: t = 60*senθ (6);
luego, sustituyes la expresión señalada (6) en la ecuación señalada (5), y queda:
5000 = 18000*senθ*cosθ, aquí divides por 9000 en ambos miembros, y queda:
5/9 = 2*senθ*cosθ, aquí aplicas la identidad del seno del doble de un ángulo, y queda:
5/9 = sen(2*θ), aquí compones con la función inversa del seno en ambos miembros (observa que tienes una solución en el primer cuadrante y otra en el segundo cuadrante), y queda:
33,749° ≅ 2*θ1, aquí divides por 2 en ambos miembros, y queda: 16,875° ≅ θ1,
146,251° ≅ 2*θ2, aquí divides por 2 en ambos miembros, y queda: 73,126° ≅ θ2.
b)
Reemplazas los valores remarcados en la ecuación señalada (6), y queda:
t1 ≅ 60*sen(16,875°) ≅ 17,417 s.
t2 ≅ 60*sen(73,126°) ≅ 57,417 s.
c)
Planteas la condición de altura máxima, y queda la ecuación:
vy = 0, sustituyes la expresión señalada (4) en el primer miembro, y queda:
300*senθ - 10*t = 0, de aquí despejas: 30*senθ = t (7);
luego, reemplazas la expresión señalada (7) en la ecuación señalada (2), y la expresión de la altura máxima queda:
yM = 300*senθ*30*senθ - 5*(30*senθ)2, resuelves coeficientes en el segundo miembro, y queda:
yM = 9000*sen2θ - 4500*sen2θ, reduces términos semejantes, y queda:
yM = 4500*sen2θ (8);
luego, reemplazas los valores angulares que obtuvimos al responder el inciso (a), y queda:
yM1 ≅ 4500*sen2(16,875°) ≅ 379,193 m,
yM2 ≅ 4500*sen2(73,126°) ≅ 4120,850 m.
Espero haberte ayudado.
-
hola buen día, estoy teniendo problemas con este ejercicio por favor necesito ayuda:
un electron se mueve en un campo magnetico cuya magnitud es de 8.7x10-5 T. El electron experimenta solamente una fuerza magnetica y tiene una aceleracion de magnitud 3.5x1014 m/s2 . En cierto instante la rapidez es de 6.8x106 m/s. Determine el angulo (menor de 90°) entre la velocidad del electron y el campo magnetico.
-
Hola buen día.. Si tengo una esfera que se gira y se traslada en condición de rodadura por un plano y luego sube una colina. Para que se mantenga la condicion de rodadura hay rozamiento en el plano, pero no en la colina. Que pasa con la esfera cuando comienza a subir la colina? ¿Es posible que la condición de rodadura se mantenga hasta que la velocidad se haga cero por el momento que genera el peso?
Raúl RC
el 9/7/18