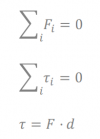-
Buenas. Estoy preparándome para la recuperación de física de campos. Estoy practicando con ejercicios de Selectividad de otros años, y este del campo gravitatorio no sabría como afrontarlo. Alguien me puede ayudar o dar una pista para saber cómo se resuelve? Gracias de antemano.
"Si sobre una partícula actúan fuerzas conservativas y no conservativas, razone cómo cambian las energías cinética, potencial y mecánica de la partícula".
Walter
el 13/1/18Para ese tipo de razonamientos tienes que saber al pie de la letra la teoria y razonar, las fuerzas conservativos son aquellas que se conservan valga la redundancia, al inicio y al final como por ejemplo la fuerza gravitatoria y las no conservativas son las hacen que sea todo 'relativo' como la fuerza de roce. Obviamente hay miles de fuerzas y dependiendo el esenario actuan de distinta manera pero me limitare a esto ya que sino seria mucho. Esto quiere decir que si las fuerzas que realizan trabajo son conservativas, la energia mecanica se conserva, la cual es la suma de la energia cinetica y potencial gravitatoria, en caso de no conservarse hay una perdida de energia ya sea en forma de calor, sonido, etc.
Es muy importante tenerlo claro, ya que el principio dice que la energia no puede ser creada ni destruida solo puede ser transformada. Lo que te piden tecnicamente es que expliques en cada caso cual seria la diferencia, por ejemplo si dejas caer una pelota de x altura y el choque con el suelo es completamente elastico y no hay perdida de energia mecanica osea queire decir que solo actuan fuerzas conservativas, lo que esto supone es que la pelota rebotara en el suelo de forma indefinida llegando a x altura siempre. En caso de colocar una fuerza no conservativa en el mismo sistema, supondria una 'perdida' de energia en la pelota por lo que con cada choque que de con el suelo su altura sera menor hasta quedar con 'cero energia' apoyada en el suelo.
-
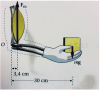
Un peso de 60 N se sostiene en la mano formando el brazo y antebrazo un ángulo de 90º como se muestra en la figura. El músculo bíceps ejerce una fuerza Fm cuya dirección dista 3,4 cm del punto de pivote O en la articulación del codo. Despreciando el peso del brazo y la mano (a) ¿cuál es la magnitud de Fm si la distancia del peso al punto de pivote es de 30 cm? (b) Determinar la fuerza ejercida sobre la articulación del codo por la parte superior del brazo.
Muchas gracias.
-
Hola.
¿Por qué si el ángulo que forman los vectores ut y ur, es decir, dl y r es siempre 90º no lo saca de la integral directamente como constante y dice que tiene 2 direcciones el campo magnético?
No lo veo.
A ver si alguien me lo pudiera explicar.
Muchas gracias.
Saludos.
-
Un hombre de 80 kg está de pie sobre una balanza de resorte sujeta al suelo de un ascensor. La balanza está calibrada en newtons. ¿Qué peso indicará la balanza cuando (a) el ascensor se mueve con una aceleración a hacia arriba; (b) el ascensor se mueve con una aceleración descendente a’; (c) el elevador se mueve hacia arriba a 29 m/s, mientras su velocidad decrece a razón de 8 m/s2 ?
Gracias
Antonio Silvio Palmitano
el 13/1/18Observa que sobre el hombre actúan dos fuerzas verticales (observa que consideramos g = 10 m/s2):
Peso: P = M*g =80*10 = 800 N, con sentido hacia abajo;
Acción normal de la balanza: N, con sentido hacia arriba;
y observa que la indicación de la balanza corresponde a la reacción que el hombre ejerce sobre ella, cuyo módulo es N.
Luego, establece un eje de posiciones OY vertical, con sentido positivo hacia arriba.
1)
Planteas la Segunda Ley de Newton (observa que indicamos con a al módulo de la aceleración), y queda:
N - P = M*a, haces pasaje de término, y queda:
N = M*a + P, sustituyes la expresión del módulo del peso del hombre, y queda;
N = M*a + M*g, extraes factor común, y queda:
N = M*(a + g), y solo queda que reemplaces valores.
2)
Planteas la Segunda Ley de Newton (observa que indicamos con a al módulo de la aceleración), y queda:
N - P = M*(-a), haces pasaje de término, y queda:
N = M*(-a) + P, sustituyes la expresión del módulo del peso del hombre, y queda;
N = M*(-a) + M*g, extraes factor común, y queda:
N = M*(-a + g), y solo queda que reemplaces valores.
3)
Planteas la Segunda Ley de Newton (observa que indicamos con 8 m/s2 al módulo de la aceleración), y queda:
N - P = M*(-a), haces pasaje de término, y queda:
N = M*(-a) + P, sustituyes la expresión del módulo del peso del hombre, y queda;
N = M*(-a) + M*g, extraes factor común, y queda:
N = M*(-a + g), reemplazas valores y queda:
N = 80*(-8+10) = 80*2 = 160 N.
Espero haberte ayudado.
-
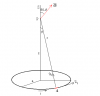
¿Cómo puedo calcular la velocidad orbital para la órbita 1 si desconozco el valor del radio terrestre (no te.lo dan y no puedo usarlo entonces) y solo conozco la altura desde la superficie terrestre+
Antonio Silvio Palmitano
el 13/1/18Vamos con una orientación.
Puedes plantear que la fuerza de atracción gravitatoria que ejerce la Tierra sobre el satélite es igual a la fuerza centrípeta que lo mantiene en órbita, por lo que tienes que los módulos de dichas fuerzas son iguales (observa que expresamos los módulos de las aceleraciones centrípetas en las órbitas en función de los módulos de las velocidades tangenciales y de los radios orbitales):
1)
Ms*v12/R1 = G*MT*Ms/R12, aquí simplificas, y queda: v12 = G*MT/R1,
observa que tienes todos los datos, y que el radio orbital inicial (que se mide desde el centro de la Tierra) es:
R1 = 10000 Km = 107 m;
2)
Ms*v22/R2 = G*MT*Ms/R22, aquí simplificas, y queda: v22 = G*MT/R2,
observa que tienes todos los datos, y que el radio orbital final (que se mide desde el centro de la Tierra) es:
R2 = 12000 Km = 1,2*107 m;
y puedes despejar luego los valores de los módulos de las velocidades orbitales.
Espero haberte ayudado.
-
Buenas, cómo se realiza el siguiente ejercicio? Muchas gracias.
La siguiente figura muestra el aspecto de un proyectil un instante después de haber estallado en tres fragmentos. ¿Cuál era la velocidad del proyectil un instante antes de su explosión?

Antonio Silvio Palmitano
el 12/1/18Establece un sistema de referencia con eje OX con la dirección y el sentido de v3, y eje OY con la dirección y el sentido de v2.
Luego, plantea la expresión del vector velocidad antes del estallido:
vi = < vix , viy >;
y la cantidad de movimiento (impulso) inicial queda (observa que la masa del proyectil es 4*M):
pi = 4*M*vi = 4*M*< vix , viy >.
Luego, plantea la cantidad de movimiento final del sistema formado por los tres fragmentos (observa que las velocidades tiene una de sus componentes iguales a cero):
pf = 2*M*< 0 , -v1 > + M*< 0 , v2 > + M*< v3 , 0 >,
reemplazas la expresión de v2 que tienes en tu enunciado, y queda:
pf = 2*M*< 0 , -v1 > + M*< 0 , 2*v1 > + M*< v3 , 0 >.
Luego, como durante el estallido no actúan fuerzas exteriores al proyectil, puedes plantear que la cantidad de movimiento se conserva, y queda la ecuación vectorial:
pi = pf,
sustituyes expresiones, y queda:
4*M*< vix , viy > = 2*M*< 0 , -v1 > + M*< 0 , 2*v1 > + M*< v3 , 0 >,
divides por 4*M en todos los términos de la ecuación, y queda:
< vix , viy > = (1/2)*< 0 , -v1 > + (1/4)*< 0 , 2*v1 > + (1/4)*< v3 , 0 >,
resuelves productos en los términos del segundo miembro, y queda:
< vix , viy > = < 0 , -(1/2)*v1 > + < 0 , (1/2)*v1 > + < (1/4)*v3 , 0 >,
resuelves la suma vectorial en el segundo miembro, y queda:
< vix , viy > = < (1/4)*v3 , 0 >,
por lo que tienes que la expresión vectorial de la velocidad del proyectil antes del estallido queda:
vi = < (1/4)*v3 , 0 >, cuyo módulo queda expresado: |vi| = (1/4)*|v3|.
Espero haberte ayudado.
-
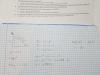 hola!! Alguien podria corregirme el ejercicio 9 porfavor, y si lo tengo mal ayudarme a hacerlo. Muchas gracias de antemano
hola!! Alguien podria corregirme el ejercicio 9 porfavor, y si lo tengo mal ayudarme a hacerlo. Muchas gracias de antemanoAnxan
el 17/1/18Hola, deberías empezar por dibujar las fuerzas que aparecen en el bloque para ayudarte a resolver el problema.
como sabes hay una fuerza de rozamiento que tienes dibujada que va en sentido contrario al movimiento del bloque, tambien deberias dibujar el peso que es perpendicular al suelo, (ojo: no al plano inclinado). tambien tienes una componente que es la normal N que esta si es perpendicular al plano. una vez dibujadas estas fuerzas descompones el peso en px y py, que mas tarde te servira para hallar el valor de la Normal.
-la de trabajo en este caso es: W=-Fr*d, donde Fr=(coeficiente de rozamiento)*normal
-la normal es igual a Py, por lo tanto, la normal es igual a m*g*cos(angulo)
-sustituimos en la formula de trabajo, donde nos queda que: W=-(coeficiente de rozamiento)*m*g*cos(angulo) *deslazamiento
El calculo del desplazamiento lo tienes bien hecho, y sale 8metros.
-sustituimos los datos en la formula de W= -0,25*5*9,8*cos(30)*8=-84,8J(julios)
[nota: los newtons solo se le aplican a las fuerzas, en cuanto energias y trabajo la unidad es Julios]
Un saludo.
-
Antonio Silvio Palmitano
el 13/1/18A)
Observa que la aceleración tiene componente radial (centrípeta), y que no tiene componente tangencial,
por lo que este caso corresponde a Movimiento Circular Uniforme.
Luego, tienes para la aceleración tangencial:
aT = dv/dt = 0.
Luego, plantea la expresión del módulo de la aceleración centrípeta en función del módulo de la velocidad tangencial y del radio de la trayectoria:
|v|2/R = |acp|, haces pasaje de divisor como factor, y queda:
|v|2 = R*|acp|, haces pasaje de potencia como raíz, y queda:
|v| = √(R*|acp|), sustituyes, y queda
|v| = √(5*20) = √(100) = 10 m/s.
Luego, plantea la expresión del módulo de la velocidad angular en función del módulo de la velocidad tangencial y del radio de la trayectoria:
|ω| = |v|/R= 10/5 = 2 rad/s.
Luego, plantea la expresión de la frecuencia de giro en función del módulo de la velocidad angular:
f = |ω|/(2π) = 2/(2π) = 1/π Hz.
Luego, plantea la expresión del periodo de giro en función de la frecuencia:
T = 1/f = π s.
B)
Observa que la aceleración tiene componente tangencial con igual sentido que la velocidad tangencial, por lo que este caso corresponde a Movimiento Circular Uniformemente Acelerado.
|aT| = a*sen(30°) = 30*(1/2) = 15 m/s2, de donde tienes: dv/dt = 15 m/s2.
|acp| = a*cos(30°) = 30*( √(3)/2 ) = 15*√(3) m/s2,
Luego, plantea la expresión del módulo de la aceleración centrípeta en función del módulo de la velocidad tangencial y del radio de la trayectoria:
|v|2/R = |acp|, haces pasaje de divisor como factor, y queda:
|v|2 = R*|acp|, haces pasaje de potencia como raíz, y queda:
|v| = √(R*|acp|), sustituyes, y queda
|v| = √( 5*15*√(3) ) = √( 75*√(3) ) ≅ 11,398 m/s.
C)
Observa que la aceleración tiene componente tangencial con sentido opuesto a la velocidad tangencial, por lo que este caso corresponde a Movimiento Circular Uniformemente Desacelerado.
|aT| = a*sen(45°) = 50*( √(2)/2 ) = 25*√(2) m/s2, de donde tienes: dv/dt = 25*√(2) m/s2.
|acp| = a*cos(45°) = 50*( √(2)/2 ) = 25*√(2) m/s2.
Luego, plantea la expresión del módulo de la aceleración centrípeta en función del módulo de la velocidad tangencial y del radio de la trayectoria:
|v|2/R = |acp|, haces pasaje de divisor como factor, y queda:
|v|2 = R*|acp|, haces pasaje de potencia como raíz, y queda:
|v| = √(R*|acp|), sustituyes, y queda
|v| = √( 5*25*√(2) ) = √( 125*√(2) ) ≅ 13,296 m/s.
Espero haberte ayudado.
-
Hola! Siempre me he preguntado, que causa la gravedad, el efecto lo dejó claro y explícito Isaac Newton, sobre la causa, sólo habló Nikola Tesla, el inventor al cuál mas patentes le fueron usurpadas y el cuál no aparece en los textos de física, aunque hay unidades que llevan su nombre, jamás se demostró que era una fuerza de atracción, pues pudiera ser de empuje... Alguien que opine al respecto???