-
Justifica si las siguientes afirmaciones son verdaderas o falsas:
a) Sienpre que la suma de las fuerzas externas a un sistema sean nulas, el momento angulas del sistema permanece constante
b) siempre que la suma de las fuerzas externas a un sistema no sean nulas, el momento angular del sistema no permanece constante
Indica de forma razonada si las siguientes afirmaciones son verdaderas o falsas:
a). Si el campo electroestático es nulo en toda región del espacio, también lo es el potencial electroestático
b) Si el flujo de campo de eléctrico a través de una superficie cerrada es nulo, el campo eléctrico en el interior de la superficie cerrada también es nulo
Antonio Silvio Palmitano
el 13/1/18Vamos con una orientación.
1)
a)
Imagina una barra homogénea, sobre la que actúan dos fuerzas paralelas perpendiculares a ella, pero con sentido contrario, aplicadas en sus extremos.
Aquí tienes que la suma de fuerzas es nula, pero tienes que la suma de sus momentos con respecto a un eje de giros perpendicular al plano al que pertenecen las fuerzas no es nulo, pero el Momento Angular Total no lo es.
b)
Imagina una barra homogénea, sobre la que actúan dos fuerzas paralelas perpendiculares a ella, pero con igual sentido, aplicadas en sus extremos.
Aquí tienes que la suma de fuerzas no es nula, pero tienes que la suma de sus momentos con respecto a un eje de giros perpendicular al plano al que pertenecen las fuerzas si es nulo, por lo que el Momento Angular Total es nulo y, por lo tanto, constante.
2)
a)
Recuerda la ecuación que vincula el módulo del campo electrostático con el potencial electrostática:
dV/dr = E, luego, como el campo es nulo, tienes la ecuación:
dV/dr = 0, expresas al diferencial de potencial en función del diferencial de radio (distancia), y queda:
dV = 0*dr, integras, y queda:
V = constante,
por lo que tienes que el potencial puede tomar cualquier valor, pero constante para todo punto del espacio.
b)
En este caso, imagina una superficie cerrada en forma de cubo, que es atravesada por un campo electrostático cuyas líneas de fuerza son paralelas.
Observa que aquí tienes que la cantidad de líneas de fuerza"entrantes" al sólido limitado por la superficie cerrada es igual a la cantidad del líneas de fuerza "salientes", por lo que tienes que el flujo total es igual a cero, pero el campo no es nulo.
Espero haberte ayudado.
-
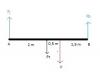
Juan y Betina transportan un bloque de 60 kg sobre una tabla de 4 m como indica la figura. La masa de la tabla es de 10 kg. Como Juan pasa la mayor parte de su tiempo leyendo libros de cocina, mientras Betina practica gimnasia, sitúan el bloque a 2,5 m de Juan y a 1,5 m de Betina. Determinar la fuerza en newtons ejercida por cada uno para trasportar el bloque.
Antonio Silvio Palmitano
el 12/1/18Indicamos en la imagen cuáles son las fuerzas que están aplicadas sobre la tabla, cuyos módulos son (observa que consideramos g = 10 m/s2):
P = 60*10 = 600 N (peso del bloque),
Pt = 10*10 = 100 N (peso de la tabla),
Fj = a determinar (fuerza ejercida por Juan),
Fb = a determinar (fuerza ejercida por Betina).
Luego, considera un eje OY vertical con sentido positivo hacia arriba, y plantea la condición de equilibrio traslacional, ya que la tabka no se desplaza en la dirección de las fuerzas:
Fj + Fb - P - Pt = 0, haces pasajes de términos, reemplazas los valores conocidos, resuelves, y queda:
Fj + Fb = 700, haces pasaje de término, y queda:
Fj = 700 - Fb (1).
Luego, considera positivo al sentido de giro antihorario, y plantea la condición de equilibrio rotacional, ya que la barra no gira (observa que consideramos un eje de giros perpendicular a la figura, que pasa por el punto A), tomas momentos de fuerzas (o torques), y queda:
MFj + MP + MFb + MPt = 0,
cancelas el primer término (observa que es igual a 0 porque la fuerza Fj está aplicada en el eje de giros), y queda:
MP + MFb + MPt = 0,
sustituyes las expresiones de los momentos de fuerzas, y queda:
-600*2,5 + Fb*4 - 2*100= 0,
resuelves y reduces los términos numéricos, haces pasaje de término, y queda:
Fb*4 = 1700,
haces pasaje de factor como divisor, y queda:
Fb = 425 N, que es el módulo de la fuerza ejercida por Betina;
luego, reemplazas en la ecuación señalada (1), resuelves, y queda:
Fj = 275 N, que es el módulo de la fuerza ejercida por Juan.
Espero haberte ayudado.
-
En un juego de billar, la bola golpeada por el taco, con una velocidad inicial de 5 m/s, realiza un choque elástico con la bola ocho, que está inicialmente en reposo. Después del choque, la bola 8 se mueve formando un angulo de 30° con la bola golpeada. Suponer que las bolas tienen la misma msa. a) determinar la direccion del movimiento de esta última después de la colisión. b) calcular la velocidad de cada bola inmediatamente después de la colisión. respuestas: a) 60° b) V cf =2.5 m/s / V8=4.33 m/s
Yo lo plantee de la siguiente manera:
m1=m2=m Vo1= 5m/s Vo2= 0 m/s &=30° entonces:
mVo1 + mVf2 = mVf1 + mVf2 ===> Vo1 = Vf1 + Vf2
m(Vo1^2)/2 + m(Vo2^2)/2 = m(Vf1^2)/2 + m(Vf2^2)/2 =======> Vo1^2 = Vf1^2 + Vf2^2
Pero cuando sustitui todos lo valores la Vf2 me dio 5m/s y no es lo que piden. Ademas no se como plantear la pregunta de la dirección.
Antonio Silvio Palmitano
el 13/1/18Vamos con una orientación.
Llamemos "bola 1" a la bola golpeada por el taco, "bola 8" a la otra bola, y llamemos M a sus masas.
Luego, plantea las expresiones vectoriales de las velocidades antes y después del choque entre las dos bolas.
Antes del choque (observa que la bola 8 está en reposo):
v10 = < 5 , 0 >, cuyo módulo queda: |v10| = 5;
v80 = < 0 , 0 >, cuyo módulo queda: |v80| = 0.
Después del choque (observa que la bola 8 se mueve formando un ángulo de 30° con la dirección de la bola 1 antes del choque, y que llamamos α al ángulo que forma la dirección de la bola 1 con respecto a su dirección antes del choque):
v1f = < v1*cosα , v1*senα >, cuyo módulo queda: |v1f| = v1;
v8f = < v8*cos(30°) , v8*sen(30°) >, cuyo módulo queda: |v8f| = v8.
Luego, como el choque es elástico, tienes que se conserva la cantidad de movimiento (o impulso) y también la energía, por lo que tienes el sistema de ecuaciones (observa que la primera ecuación es vectorial y la segunda es escalar):
M*v1f + M*v8f = M*v10 + M*v80,
(1/2)*M*|v1f|2 + (1/2)*M*|v8f|2 = (1/2)*M*|v10|2 + (1/2)*M*|v80|2.
Luego, divides por M en todos los términos de la primera ecuación, multiplicas por 2/M en todos los términos de la segunda ecuación, y queda:
v1f + v8f = v10 + v80,
|v1f|2 + |v8f|2 = |v10|2 + |v80|2.
Luego, sustituyes expresiones vectoriales en la primera ecuación, sustituyes expresiones escalares en la segunda ecuación, y queda:
< v1*cosα , v1*senα > + < v8*cos(30°) , v8*sen(30°) > = < 5 , 0 > + < 0 , 0 >,
v12 + v82 = 52 + 02.
Cancelas términos nulos en ambas ecuaciones, resuelves el segundo miembro de la segunda ecuación, y queda:
< v1*cosα , v1*senα > + < v8*cos(30°) , v8*sen(30°) > = < 5 , 0 >,
v12 + v82 = 25.
Descompones la primera ecuación (vectorial) en dos ecuaciones escalares (una para cada componente), y queda:
v1*cosα + v8*cos(30°) = 5,
v1*senα + v8*sen(30°) = 0,
v12 + v82 = 25,
que es un sistema de tres ecuaciones con tres incógnitas, que son los módulos de las velocidades finales de las bolas y el ángulo que forma la velocidad de la bola 1 con respecto a su velocidad antes del choque.
Queda que continúes y termines la tarea y, si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Raúl RC
el 31/1/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
 Hola, querría saber como se resuelven estos dos apartados porque no me da lo mismo que en la solución. Muchas gracias un saludo
Hola, querría saber como se resuelven estos dos apartados porque no me da lo mismo que en la solución. Muchas gracias un saludo Antonio Silvio Palmitano
el 11/1/18Puedes plantear la expresión vectorial de la posición en función del tiempo:
r(x) = < At , (At)2 > = < At , A2t2 >, con t ≥ 0 (observa que se cumple la condición: r(0) = < 0 , 0 >)
Luego, derivas con respecto al tiempo, y tienes la expresión de la función vectorial velocidad:
v(t) = r ' (t) = < A , 2A2t> (observa que la primera componente es constante),
y a partir de la condición de tu enunciado (vx = 3 m/s) tienes: A = 3 m/s;
luego, sustituyes en las expresiones vectoriales, y quedan:
r(t) = < 3t , 9t2 > (1).
v(t) = < 3 , 18t > (2).
Luego, derivas la velocidad con respecto al tiempo, y la expresión vectorial de la aceleración queda:
a(t) = v ' (t) = < 0 , 18 > (3).
Luego, tienes el valor de la primera componente de la función posición (x = 60 cm = 0,60 m), por lo que puedes plantear, a partir de la primera componente de la expresión señalada (1):
3t = 0,60, haces pasaje de factor como divisor, y queda: t = 0,20 s;
luego, evalúas en las expresiones señaladas (1) (2) (3), y queda:
r(0,20) = < 0,60 , 0,36 > (expresada en m);
v(0,20) = < 3 , 3,6 > (expresada en m/s), cuyo módulo queda |v(0,20)| = √(32 + 3,62) = √(21,96) ≅ 4,686 m/s;
a(0,20) = < 0 , 18 > (expresada en m/s2), cuyo módulo queda: |a(0,20) = √(02 + 182) = √(182) = 18 m/s2.
Espero haberte ayudado.
-
Javier Alonso Delgado
el 12/1/18La aceleración tangencial la sacas haciendo la derivada del módulo de la velocidad en función del tiempo. Luego, la normal la despejas teniendo en cuenta que el cuadrado del módulo de la aceleración total es la suma de los cuadrados de la aceleración normal y tangencial. Una vez hallada la normal, despejas el radio sabiendo que an=v2/R
Antonio Silvio Palmitano
el 12/1/18a)
Derivas con respecto al tiempo, y tienes el vector velocidad:
v(t) = < 1 , t , 1 >, cuyo módulo queda: |v(t)| = √(t2+2).
luego, derivas con respecto al tiempo, y tienes el vector aceleración:
a(t) = < 0 , 1 , 0 >, cuyo módulo queda: |a(t)| = 1.
b)
Tienes las ecuaciones cartesianas paramétricas de la trayectoria a partir de las componentes del vector posición que tienes en tu enunciado:
x = t,
y = (1/2)*t2,
z = t,
con t ∈ R;
luego, sustituyes el parámetro, a partir de la expresión de la primera ecuación, en las dos últimas ecuaciones, y queda:
y = (1/2)*x2,
z = x;
y tienes las ecuaciones cartesianas de la trayectoria, que es la curva intersección entre un cilindro parabólico que contiene aleje OZ y un plano que contiene al eje OY.
c)
Plantea la expresión del vector tangente unitario:
T(t) = v(t)/|v(t)| = < 1 , t , 1 >/√(t2+2) = < 1/√(t2+2) , t/√(t2+2) , 1/√(t2+2) >;
luego, plantea a la componente tangencial de la aceleración como el producto escalar entre el vector aceleración y el vector tangente unitario:
|aT(t)| = a(t) • T(t) = < 0 , 1 , 0 > • < 1/√(t2+2) , t/√(t2+2) , 1/√(t2+2) > = t/√(t2+2).
d)
Plantea la expresión de la componente normal de la aceleración (o aceleración centrípeta) en función del módulo de la aceleración y del módulo de la componente tangencial de la aceleración:
|aN(t)|2 = |a(t)|2 - |aT|2 = 12 - ( t/√(t2+2) )2 = 1 - t2/(t2+2) = (t2+2 - t2)/(t2+2) = 2/(t2+2);
luego, haces pasaje de potencia como raíz, y queda:
|aN(t)| = √( 2/(t2+2) ) = √(2)/√(t2+2).
e)
Puedes plantear la expresión de la función curvatura en función de la velocidad y de la aceleración:
κ(t) = |v(t) x a(t)|/|v(t)|3,
sustituyes expresiones, y queda:
κ(t) = |< 1 , t , 1 > x < 0 , 1 , 0 >|/√(t2+2) = |< -1 , 0 , 1 >|/√(t2+2) = √(2)/√(t2+2);
luego, planteas la expresión del radio de curvatura en función de la curvatura, y queda:
R(t) = 1/κ(t) = √(t2+2)/√(2).
f)
Recuerda que el vector aceleración tangencial tiene la dirección del vector tangente unitario, por lo que puedes plantear:
aT(t) = |aT(t)|*T(t) = ( t/√(t2+2) )*< 1 , t , 1 >/√(t2+2) = < t , t2 , t >/(t2+2) = < t/(t2+2) , t2/(t2+2) , t/(t2+2) >.
Luego, te dejo una orientación:
plantea la expresión del vector normal unitario:
N(t) = T ' (t) / |T ' (t)|;
y, luego, plantea la expresión del vector aceleración normal (o centrípeta) como el producto entre el módulo de la aceleración normal por el vector normal unitario:
aN(t) = |aN(t)|*N(t);
queda que hagas el desarrollo.
Espero haberte ayudado.
-
Walter
el 11/1/18Primero tienes que identificar el centro geometrico de cada figura:
Hay un cuadrado y un rectangulo por lo que sera facil, del cuadrado(0,1; 0,1) y el rectangulo(0,4; 0,2). Luego se establece el origen, en este caso lo pondre en el centro del rectangulo por comodidad.
Xcmx=(Ax1·Xx1+Axn·Xxn)/(∑Ax)
Ax1= 0,2 · 0,2 = 0,4
Xx1= 0,4 - 0,2 = 0,2
Ax2= 0,8 · 0,4 = 0,32
Xx2= 0
Xcmy=(Ay1·Xy1+Ayn·Xyn)/(∑Ay)Ay1= 0,2 · 0,2 = 0,04
Xy1= 0,2 + 0,1 = 0,3
Ay2= 0,8 · 0,4 = 0,32
Xy2= 0
Respuesta: El centro de masa esta en (0,02; 0,03)m colocando el origen en el centro del rectangulo, en caso de ponerlo en la esquina inferior izquierda tendrias que aumentar la distancias (42,22; 23,33)cm
Iker
el 11/1/18Antonio Silvio Palmitano
el 11/1/18Vamos con una orientación.
Consideramos que la distribución de masa es homogénea, y que su densidad de masa es: k Kg/m2.
Luego, puedes establecer un sistema de referencia cartesiano OXY con origen en el vértice inferior izquierdo del rectángulo mayor, con eje OX horizontal con sentido positivo hacia la derecha, y eje OY vertical, con sentido positivo hacia arriba.
Luego, como la distribución de masa es homogénea, puedes plantear que la posición del centro de masas de cada rectángulo coincide con la posición correspondiente a su centro geométrico, cuya abscisa, por ejemplo, será el promedio de las abscisas de los vértices inferiores, y cuya ordenada será, por ejemplo, el promedio de las ordenadas de los vértices laterales izquierdos.
Luego, tienes para el rectángulo mayor:
MM = k*AM = k*0,8*0,4 = 0,32*k (expresada en Kg),
xM = (0+0,8)/2 = 0,8/2 = 0,4 m,
yM = (0+0,4)/2 = 0,4/2 = 0,2 m;
por lo que el centro de masas para este rectángulo queda expresado; CM( 0,4 , 0,2 ).
Luego, tienes para el rectángulo menor:
Mm = k*Am = k*0,2*0,2 = 0,04*k (expresada en Kg),
xm = (0,6+0,8/2 = 1,4/2 = 0,7 m,
ym = (0,4+0,6)/2 = 1/2 = 0,5 m;
por lo que el centro de masas para este rectángulo queda expresado; Cm( 0,7 , 0,5 ).
Luego, puedes plantear que las masas de los rectángulos están concentradas en sus centros de masas,
y luego plantear las coordenadas del centro de masa correspondiente a toda la tabla de madera:
xc = (MM*xM + Mm*xm) / (MM + Mm),
yc = (MM*yM + Mm*ym) / (MM + Mm);
luego, sustituyes, y queda
xc = (0,32*k*0,4 + 0,04*k*0,7) / (0,32*k + 0,04*k) = (0,128*k + 0,028*k)/(0,36*k) = (0,156*k)/(0,36*k) ≅ 0,433 m,
yc = (0,32*k*0,2 + 0,04*k*0,5) / (0,32*k + 0,04*k) = (0,064*k + 0,002*k)/(0,36*k) = 0,066*k)/(0,36*k) ≅ 0,183 m;
por lo que el centro de masas del tablón queda expresado: C( 0,433 , 0,183 ).
Espero haberte ayudado.
Walter
el 12/1/18Disculpa por no haberlo mencionado, la ecuacion que se usa es Xcm=(A1·X1+A2·X2+...+An·Xn)/(A1+A2+...+An)
Xcm = Es la distancia del centro de masa que buscas.
A = Es el area.
X = Es la distancia del origen al centro de la figura.
Como dice Antonio tambien se puede usar la misma ecuacion en caso de tener la masa, solo se cambiaria el area por la masa. Gracias por la correccion, me hiciste dar cuenta que el origen no se lo puede hubicar en el centro de la figura, tendras que colocalo en otro lado para no modificar la ecuacion. Como lo plante Antonio es lo correcto, solo que en vez de usar la masa utiliza el area.
Suerte!!! -
¿Cómo podría realizar el siguiente ejercicio? Un saludo y muchas gracias.
Un peso de 60 N se sostiene en la mano formando el brazo y antebrazo un ángulo de 90º como se muestra en la figura. El músculo bíceps ejerce una fuerza Fm cuya dirección dista 3,4 cm del punto de pivote O en la articulación del codo. Despreciando el peso del brazo y la mano (a) ¿cuál es la magnitud de Fm si la distancia del peso al punto de pivote es de 30 cm? (b) Determinar la fuerza ejercida sobre la articulación del codo por la parte superior del brazo.
-
 Se enrolla una cuerda alrededor de dos poleas de diferentes radios. Calcular el peso del bloque para que tenga una velocidad de 2m/s después de 4s.
Se enrolla una cuerda alrededor de dos poleas de diferentes radios. Calcular el peso del bloque para que tenga una velocidad de 2m/s después de 4s.m1= 1kg
r1=0.5m
m2= 2kg
r2= 1mRaúl RC
el 31/1/18Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Buenos Dias,
Soy estudiante de ingenieria en la universidad y me harian falta clases de teoria sobre el solido rigido.
No entiendo de donde viene que Lo= I + OP x p