-
HOLA A TODOS COMO ESTAN UN SALUDO ENORME
TENGO UN PROBLEMILLA CON UN EJERCICIO DE FISICA EL CUAL APLICA LA SEGUNDA LEY DE NEWTON SOBRE EL MOVIMIENTO , ESPECIFICAMENTE ESTE EXPERIMENTO SE LLAMA "LA BASCULA EN UN ELEVADOR" Y PUES A PESAR DE QUE YA TENGO LAS RESPUESTAS A LAS PREGUNTAS DE ESTE EJERCICIO RESALTADAS NO LOGRO LLEGAR A LAS MISMAS POR NINGUN LADO , QUISIERA VER SI A LO MEJOR USTEDES LO PILLAN Y ME AYUDAN PORFAVOR..
Antonio Silvio Palmitano
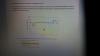
el 24/7/17Observa que la báscula ejerce sobre la persona una acción normal vertical hacia arriba, y que la Tierra ejerce sobre ella el peso, vertical hacia abajo.
Considera un sistema de referencia con eje OY vertical, con sentido positivo hacia abajo y origen en la parte más alta del edificio.
Luego tienes:
a) periodos donde el elevador está en reposo (de 0 a 2s y de 24 a 26 s) o se mueve con velocidad constante (de 4s a 22s),
en el que la báscula ejerce una acción normal cuyo módulo es: Na = 80 Kgf = 80*9,8 = 784 N;
b) un periodo donde el elevador se mueve con aceleración ab (de 2s a 4s),
en el que la báscula ejerce una acción normal cuyo módulo es: Nb = 60 Kgf = 60*9,8 = 588 N;
c ) un periodo donde el elevador se mueve con aceleración ac (de 22s a 24s),
en el que la báscula ejerce una acción normal cuyo módulo es: Nc = 100 Kgf = 100*9,8 = 980 N.
a)
Plantea la Primera Ley de Newton:
P - Na = 0, de donde despejas: P = Na = 80 Kgf = 80*10 = 800 N, y observa que la masa del estudiante es: M = P/g = 800/10 = 80 Kg.
b)
Observa que tienes en el gráfico: Nb = 60 Kgf = 60*10 = 600 N,
luego, plantea la Segunda Ley de Newton:
P - Nb = M*ab, reemplazas valores y queda:
800 - 600 = 80*ab, de donde despejas: ab = 2,5 m/s2.
c)
Observa que tienes en el gráfico: Nc = 100 Kgf = 100*10 = 1000 N,
luego, plantea la Segunda Ley de Newton:
P - Nc = M*ac, reemplazas valores y queda:
800 - 1000 = 80*ac, de donde despejas: ac = - 2,5 m/s2.
Luego, tienes cinco etapas de movimiento:
1) El elevador se encuentra en reposo en la parte más alta del edificio (y = 0) entre t = 0 y t = 2s.
2) El elevador acelera entre t = 2s y t = 4s.
3) El elevador se desplaza con velocidad constante entre t = 4s y t = 22s.
4) El elevador desacelera entre t = 22s y t = 24 s.
5) El elevador se encuentra en reposo en la parte más baja del edificio (y = h) entre t = 24s y t = 26s.
Luego plantea las expresiones de posición final y de la velocidad final del elevador para cada etapa (observa que los datos finales de una etapa son los datos iniciales para la etapa siguiente, y observa que consideramos para el módulo de la aceleración gravitatoria terrestre: g = 10 m/s2):
1)
y1 = 0, y v1 = 0.
2)
y2 = 0 + 0*(4 - 2) + (1/2)*2,5*(4 - 2)2 = 0 + 0 + 5 = 5 m, y v2 = 0 + 2,5*(4 - 2) = 5 m/s.
3)
y3 = 5 + 5*(22 - 4) = 5 + 90 = 95 m, y v3 = 5 m/s.
4)
y4 = h = 95 + 5*(24 - 22) + (1/2)*(- 2,5)*(24 - 22)2 = 95 + 10 - 5 = 100 m, y v4 = 5 - 2,5*(4 - 2) = 0.
5)
y5 = h = 100 m, y v5 = 0.
Luego, tienes que la altura del edificio es cien metros.
Espero haberte ayudado.
-
Alguien me puede guiar en el apartado e), es decir, como obtiene la ecuacion de la circunferencia????

Antonio Silvio Palmitano
el 24/7/17Puedes plantear para las componentes del vector posición:
x = 2*sen(3t)
y = 2*cos(3t),
luego elevas al cuadrado en ambos miembros y queda:
x2 = 4*sen2(3t)
y2 = 4*cos2(3t),
luego sumas miembro a miembro (observa que extraemos factor común entre los segundos miembros) y queda:
x2 + y2 = 4*( sen2(3t) + cos2(3t) ),
resuelves la identidad trigonométrica en el agrupamiento del segundo miembro (observa que es igual a 1) y queda:
x2 + y2 = 4.
Espero haberte ayudado.
-
Raúl RC
el 24/7/17Deberás hallar el calor específico como un incremento utilizando las temperaturas que te dan, es decir, siendo CF el calor especifico usando la temperatura final y CI el inicial usando la temperatura inicial:
ΔC=CF-CI
Después bastaría con que aplicaras la ecuacion Q=m·ΔC·ΔT
Antonio Silvio Palmitano
el 25/7/17Observa que el calor específico es una función de la temperatura,
por lo que puedes partir de la ecuación diferencial del calor en función de la masa, el calor específico y la temperatura:
dQ = M*c*dT,
sustituyes valores y expresiones y queda (M = 1 Kg = 1000 g, c = 1 + 0,5*T):
dQ = 1000*(1 + 0,5*T)*dT,
distribuyes en el segundo miembro y queda:
dQ = 1000*dT + 500*T*dT,
integras en ambos miembros (observa que indicamos con corchetes que debes evaluar con la Regla de Barrow entre 20 °C y 50 °C).
Q = [ 1000*T + 250*T2 ],
evalúas y queda:
Q = (50000 + 625000) - (20000 + 100000) = 675000 - 120000 = 555000 cal = 555 Kcal.
Espero haberte ayudado.
-
HOLA.. ¿Pueden ayudarme con este problema?
Tema: Gases ideales
(Pero creo que también interviene el tema de teorema de Bernoulli) -
Hola, quisiera consultar este ejercicio porque no me doy cuenta en que me estaría equivocando ya que me da que la corriente tiene un valor de 150A y deberia dar 50A. Gracias y saludos
Raúl RC
el 24/7/17 -
Hola, me he recién apuntado y estaria interesado en estudiar materias relacionadas con la electrotécnia pero no se por donde empezar. He dejado mis estudios de perito electrotecnico al segundo año en mi pais pero no puedo homologar mi titulo asi que como tengo que llevar materias que ni me importan y en catalán todo, pues... Como que no. Asi que tengo que optimizar los tiempos. Llendo al grano me sirve saber como funciona la electricidad en todas sus formas ( sobre todo a bajos voltajes en DC, funcionamiento de circuitos, transistor, sensores etc ) para que pueda luego aplicar estos conocimientos con material didactico de Arduino.
Si alguien maneja tambien lenguaje C para programaciòn, informatica, robotica o relacionados tambien estaria interesado.
Saludos.
Guillem De La Calle Vicente
el 22/7/17Ángel
el 22/7/17Para dudas muy puntuales (no para prácticas ni trabajos de clase):
Programación en C (informática), ProLog (quizá sea tu base en robótica), prácticas con osciloscopio (electrotecnia): pon dudas concretas en el foro de matemáticas (que es el que yo suelo visitar...he visto tu mensaje de casualidad)
AUNQUE TEN MUY PRESENTE QUE LOS TEMAS A LOS QUE TE REFIERES ESTÁN FUERA DE LA COMPETENCIA DE ESTA PÁGINA (así que con razón se te pondrán banderitas rojas y en cada pregunta sobre estos temas se te recordará que no estás en el foro/página adecuado).
Mucha suerte.
-
Por Favor Necesito que me ayuden a realizar este ejercicio dependo de aprobar o suspender... muchas gracias
Para un proyectil lanzado con velocidad inicial v0, formando un ́angulo α con la horizontal, deduzca expresiones generales para la altura m ́axima h y el alcance horizontal R. Calcula el ́angulo con el que habría que lanzar el proyectil para que h y R sean iguales.
Antonio Silvio Palmitano
el 21/7/17Establece un sistema de referencia OXY con origen en el punto de lanzamiento, eje OX horizontal con sentido positivo favorable al movimiento, y eje OY vertical con sentido positivo hacia arriba. Luego, consideramos como instante inicial el que corresponde al lanzamiento del proyectil, y planteamos las ecuaciones de Tiro Parabólico:
x = v0*cosα*t
y = v0*senα*t - (1/2)*g*t2
vx = v0*cosα
vy = v0*senα - g*t
a)
Plantea la condición de altura máxima (observa que en su instante correspondiente el proyectil "ni asciende ni desciende"):
vy = 0, sustituyes y queda:
v0*senα - g*t = 0, haces pasaje de término y queda:
- g*t = - v0*senα, haces pasaje de factor como divisor y queda:
t = v0*senα/g, que es el instante en que el proyectil alcanza su altura máxima,
luego sustituyes en la ecuación de altura (observa que en este instante tienes: y = h) y queda:
h = v0*senα*v0*senα/g - (1/2)*g*(v0*senα/g)2,
resuelves el segundo miembro y queda:
h = (1/2)*v02*sen2α/g, que es la expresión de la altura máxima que alcanza el proyectil.
b)
Plantea la condición de alcance (que es la posición del punto donde el proyectil vuelve a alcanzar su altura inicial):
y = 0, sustituyes y queda:
v0*senα*t - (1/2)*g*t2 = 0, multiplicas en todos los términos de la ecuación por -2/g y queda:
- 2*v0*senα*t/g + t2 = 0, extraes factor común y queda:
t*(- 2*v0*senα/g + t) = 0, de donde, por anulación de un producto, tienes dos opciones:
b1)
t = 0, que es el instante de lanzamiento,
b2)
- 2*v0*senα/g + t = 0, donde haces pasaje de término y queda:
t = 2*v0*senα/g, que es el instante en que el proyectil vuelve a tener la altura inicial,
luego sustituyes en la ecuación de posición horizontal (observa que en este instante tienes: x = R) y queda:
R = v0*cosα*2*v0*senα/g, resuelves el segundo miembro y queda:
R = v02*2*cosα*senα/g = v02*sen(2α)/g, que son expresiones del alcance del proyectil.
c)
Plantea que la altura máxima es igual al alcance:
h = R, haces pasaje de término y queda:
h - R = 0, sustituyes expresiones y queda:
(1/2)*v02*sen2α/g - v02*2*cosα*senα/g = 0, multiplicas por 2*g/v02 en todos los términos de la ecuación y queda:
sen2α - 4*cosα*senα = 0, extraes factor común y queda:
senα*(senα - 4*cosα) = 0, luego tienes dos opciones por anulación de un producto:
c1)
senα = 0, donde compones con la función inversa del seno y queda: α = 0, que no tiene sentido para este problema;
c2)
senα - 4*cosα = 0, donde haces pasaje de término y queda:
senα = 4*cosα, luego haces pasaje de factor como divisor y queda:
senα/cosα = 4, aplicas la identidad trigonométrica de la tangente y queda:
tanα = 4, luego compones con la función inversa de la tangente y queda:
α ≅ 1,3258 rad ≅ 75,938°.
Espero haberte ayudado.
-
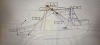
Buenas noches, quisiera que me puedan ayudar por favor no entiendo como tengo que hacer este ejercicio de poleas.
Me dicen que el bote debe pesar 8tn y determinar la fuerza de cada polea.
Gracias de antemano.
Raúl RC
el 21/7/17Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola unicoos quisiera saber si la ecuacion de torricelli Vf^2=V○^2+2 (xf-x○) siempre va ser positivo ? Ya que es una ecuaciónescalar no vectorial ??
-
Antonio Silvio Palmitano
el 21/7/17Vamos con un planteo con energías, con un ordenamiento en los pasos, y verás que arribamos a tus mismos resultados.
Puedes considerar el nivel más bajo del aro como altura igual a cero, y consideramos para el módulo de la aceleración gravitatoria terrestre: g ≅ 10 m/s2.
Luego, cuando el móvil llega al punto más bajo del aro (A), tienes que su energía potencial gravitatoria es igual a cero, y su energía mecánica es igual a su energía cinética:
EMA = EPA + ECA = M*g*yA + (1/2)*M*vA2 = 400*10*0 + (1/2)*400*152 = 0 + 45000 = 45000 J.
Luego, cuando el móvil llega al punto más alto del aro (B) tienes:
EMB = EPB + ECB = M*g*yB + (1/2)*M*vB2 = 400*10*8 + (1/2)*400*vB2 = 32000 + 200*vB2.
Luego, como despreciamos todo tipo de rozamiento, y como no actúan otras fuerzas que efectúen trabajos mecánicos, puedes plantear que la energía mecánica se conserva:
EMB = EMA, sustituyes expresiones y valores y queda:
32000 + 200*vB2 = 45000, haces pasaje de término y queda:
200*vB2 = 13000, haces pasaje de factor como divisor y queda:
vB2 = 65, haces pasaje de potencia como raíz y queda:
vB = √(65) m/s ≅ 8,062 m/s.
Luego, puedes plantear la aceleración centrípeta en el punto más alto del aro:
acpB = vB2/R = 65/4 = 16,25 m/s2.
Luego, puedes plantear la ecuación de la Segunda Ley de Newton en el punto más alto del aro:
NB + P = M*acpB, haces pasaje de término y queda:
NB = M*acpB - P, sustituyes la expresión del peso del cuerpo y queda:
NB = M*acpB - M*g, extraes factor común y queda:
NB = M*(acpB - g), reemplazas valores y queda:
NB = 400*(16,25 - 10) = 400*6,25 = 2500 N,
que es el módulo de la acción que el riel ejerce sobre el carro en el punto más alto del aro.
Espero haberte ayudado.